
IAHR
CIC
XXV CONGRESO LATINOAMERICANO DE HIDRÁULICA
SAN JOSÉ, COSTA RICA, 9 AL 12 DE SETIEMBRE DE 2012
CALIBRACIÓN DE MODELOS DE SISTEMAS DE DRENAJE URBANO
Juan G. Saldarriaga, María A. Escovar, Diego A. Páez
Centro de Investigación en Acueductos y Alcantarillados – Universidad de los Andes - Bogotá, Colombia
<jsaldarr@uniandes.edu.co>, <ma-escov@uniandes.edu.co>, <da.paez27@uniandes.edu.co>
RESUMEN:
El problema de calibración de un modelo consiste en ajustar el valor de los parámetros de
éste a fin de que sus resultados se aproximen, de manera aceptable, a los resultados medidos en el
prototipo. En el caso de modelos de redes de alcantarillado se recomienda su uso para el posterior
diseño de ampliaciones y/o operación de los elementos de control del sistema. En esta investigación
se formula una metodología para realizar la calibración hidráulica de redes de alcantarillado bajo
flujo no permanente con el uso de Algoritmos Genéticos (AG) y EPASWMM, un motor de
simulación hidráulica. Se realizó la calibración hidráulica en redes de diferente topología,
topografía y propiedades hidráulicas, encontrando resultados de alta calidad. El coeficiente de
rugosidad relativa se seleccionó como el parámetro a calibrar, evaluando la efectividad de los
resultados con el ajuste de los limnigramas medidos en el prototipo y simulados con el modelo
calibrado. Se concluye que la calibración hidráulica de redes de alcantarillado con AG es incluso
más sencilla que el proceso de calibración de redes de distribución de agua portable (RDAP).
ABSTRACT: (1
era.
hoja)
The calibration problem consists in adjusting the value of each model´s parameter looking
for a good approximation between the measured results and the simulated ones. In the case of sewer
networks models the calibration is recommended before starting a study on design of new
expansions or about the operation of the control elements on the system. This research sets out a
methodology to calibrate hydraulic sewer models under unsteady flow using Genetic Algorithms
and EPASWMM, a hydraulic simulation software. Hydraulic calibration was performed on
networks with different topology, topography and hydraulic properties, achieving high-quality
results. The relative roughness coefficient was the calibration parameter selected, and the
limnigrams measured and simulated were the results selected to evaluate the effectiveness of the
procedure. It was concluded that the hydraulic calibration of sewerage networks with Genetic
Algorithms proves to be even simpler than the calibration of water distribution networks.
PALABRAS CLAVES: Calibración, Redes de Drenaje Urbano, Algoritmos Genéticos.

INTRODUCCIÓN
Dentro de los componentes más importantes de los asentamientos urbanos modernos se
encuentran los sistemas de drenaje urbano. Estos sistemas son los encargados de recolectar aguas
residuales y lluvias, transportar dichas aguas a puntos de tratamiento donde no representen ningún
problema o incomodidad a la población y realizar el tratamiento de las aguas de manera que sus
condiciones sean aceptables para que puedan ser finalmente descargadas en cuerpos receptores. Los
modelos de estos sistemas tienen como función principal representar algún comportamiento
específico de la realidad, a fin de facilitar tareas que involucran la toma de decisiones. Orozco
(2005) resume dichas tareas en:
a) Diseño de planes maestros de alcantarillados municipales.
b) Diseño de nuevos sistemas semejantes o adicionales al existente.
c) Operación diaria de la red (parte hidráulica del sistema).
d) Ejecución de programas o algoritmos de control en tiempo real.
e) Toma de decisiones de necesidades de rehabilitación de la red.
f) Evaluación del estado de la red.
g) Ejecución de proyectos investigativos de calidad de agua, entre otros.
Todos estos posibles usos del modelo requieren que los resultados que éste entregue sean
aceptablemente cercanos a los presentados en el prototipo (realidad). Para lograr este objetivo se
hace necesario realizar la calibración del modelo. Este proceso ajusta algunos de los parámetros
para que los resultados sean más parecidos a los medidos en el prototipo. Si bien existen diferentes
planteamientos matemáticos del mencionado problema, la formulación implícita en la que se
plantea como un problema de optimización (Savic et al., 2009), ha sido comúnmente utilizada dada
la alta disponibilidad de metodologías de optimización. En el planteamiento matemático, la función
objetivo seleccionada usualmente relaciona los datos medidos con los datos calculados, de manera
que se busca minimizar la diferencia entre estos, tomando como variables de decisión los valores de
los parámetros calibrables y teniendo como restricciones las ecuaciones que rigen la hidráulica del
sistema así como posibles rangos para el valor de cada parámetro calibrable.
En el presente artículo se presentan los resultados de una investigación donde se desarrolló
una metodología de calibración de redes de alcantarillado, las cuales son parte fundamental de los
sistemas de drenaje urbano, utilizando Algoritmos Genéticos (AG) para solucionar el problema de
optimización descrito anteriormente. Para ello se procedió a realizar un análisis de sensibilidad de la
respuesta hidráulica del sistema a modificaciones en algunas características de las tuberías. Después
se hizo uso del programa GANetXL (Centre for Water Systems, 2006) para estimar los valores de
parámetros calibrables encontrados en el primer paso, determinando en el proceso la manera
recomendada de utilizar los AG.
METODOLOGÍA
El proceso de calibración se lleva a cabo mediante la variación de unos parámetros
desconocidos hasta llegar a una representación lo más cercana posible a la realidad (prototipo). La
selección de la metodología a usar depende del uso final del modelo y del grado de certidumbre
objetivo. Sin embargo, usualmente los pasos seguidos para realizar la calibración son (Orozco
2005):
1. Identificar la estructura adecuada que describa el sistema de interés.
2. Identificar los parámetros asociados con el modelo.
3. Analizar el comportamiento matemático del modelo.
4. Evaluar la calidad del modelo.
5. Analizar y estimar la incertidumbre en los resultados del modelo.

6. Evaluar escenarios de operación. Aplicar a casos de estudio.
Para seleccionar el modelo más adecuado para la representación de la realidad, se pueden
escoger modelos determinísticos, estocásticos o conceptuales (Mays, 2001, Orozco, 2005). En el
caso de sistemas de drenaje urbano, los modelos determinísticos son los más comúnmente utilizados
facilitando así el proceso de calibración. De esta manera se deben seleccionar los parámetros
calibrables, que corresponden a parámetros del modelo seleccionado que se consideren
desconocidos en el prototipo y que resulten convenientes a la hora de ajustar los resultados del
modelo con los resultados medidos.
Dentro de los parámetros que definen una tubería de una red de alcantarillado, se
encuentran: el diámetro, la rugosidad y la pendiente. Para determinar cuáles de estos son
suficientemente trascendentales para la hidráulica de la red y en qué medida, se requiere hacer un
análisis de sensibilidad que evalúe los cambios en la respuesta hidráulica producidos por cambios
en alguno de estos parámetros. Una vez seleccionados los parámetros a calibrar, se procede a
ejecutar el programa de calibración que hace uso de AG para estimar los parámetros calibrables
definidos a partir de dicho análisis. En este procedimiento se definen grupos de tuberías de manera
que el número de parámetros calibrables en una red dada, será:
[1]
donde,
es el número de parámetros calibrables del modelo,
es el número de grupos
de tuberías en que se divide la red y
es el número de parámetros calibrables por grupo, el
cuál debe corresponder con el número de parámetros calibrables de una tubería.
Una vez se conocen los parámetros a calibrar, se debe seleccionar la configuración de la
metodología de solución con AG. Es decir que se deben definir: a) El tamaño de la población
(número de redes en cada generación de los AG) , b) El número de generaciones, c) El método de
selección, d) El método de combinación, e) El método de mutación y f) La función objetivo. Para
ello se recomienda revisar diferentes estudios y realizar diferentes ejecuciones cambiando dichos
valores para determinar una configuración recomendable. Finalmente se ejecuta el procedimiento y
se comparan los resultados tanto para los mismos datos utilizados en el proceso de calibración,
como para otros resultados que permitirán cuantificar de mejor manera el error final del modelo
calibrado.
Análisis de sensibilidad
Teniendo en cuenta que las variables de decisión a la hora de hacer el análisis de
sensibilidad para un parámetro dado incluyen, el número de tuberías a modificar, y la magnitud de
dicha modificación, se realizaron pruebas que incluyeron los siguientes valores:
- Diámetro: Modificaciones en una, dos, tres y todas las tuberías de la red. Magnitudes de
variación entre -30% y +30% del diámetro del modelo, o variaciones correspondientes a
asignar a la tubería el siguiente (o el anterior) diámetro disponible en el mercado.
- Rugosidad: Modificaciones en una, dos, tres y todas las tuberías de la red. Magnitudes de
variación entre -60% y +60% de la rugosidad del modelo.
- Pendiente: Modificaciones en todas las tuberías de la red. Magnitudes de variación de -
50%, -80% y +100%.
Los modelos utilizados para realizar el análisis de sensibilidad fueron modelos hidráulicos
utilizados y/o desarrollados en el Centro de Investigaciones en Acueductos y Alcantarillados
(CIACUA) de la Universidad de Los Andes, Bogotá, Colombia. Estos modelos incluyen la red de
Girardot-Acacias que tiene un área cercana a las 96 ha y le presta el servicio de recolección de
aguas residuales y lluvias a 11,000 habitantes. La subcuenca no tiene canales abiertos ni aliviaderos
de agua lluvia y cuenta con una sola descarga, que conduce el agua captada hacia el río Bogotá. En
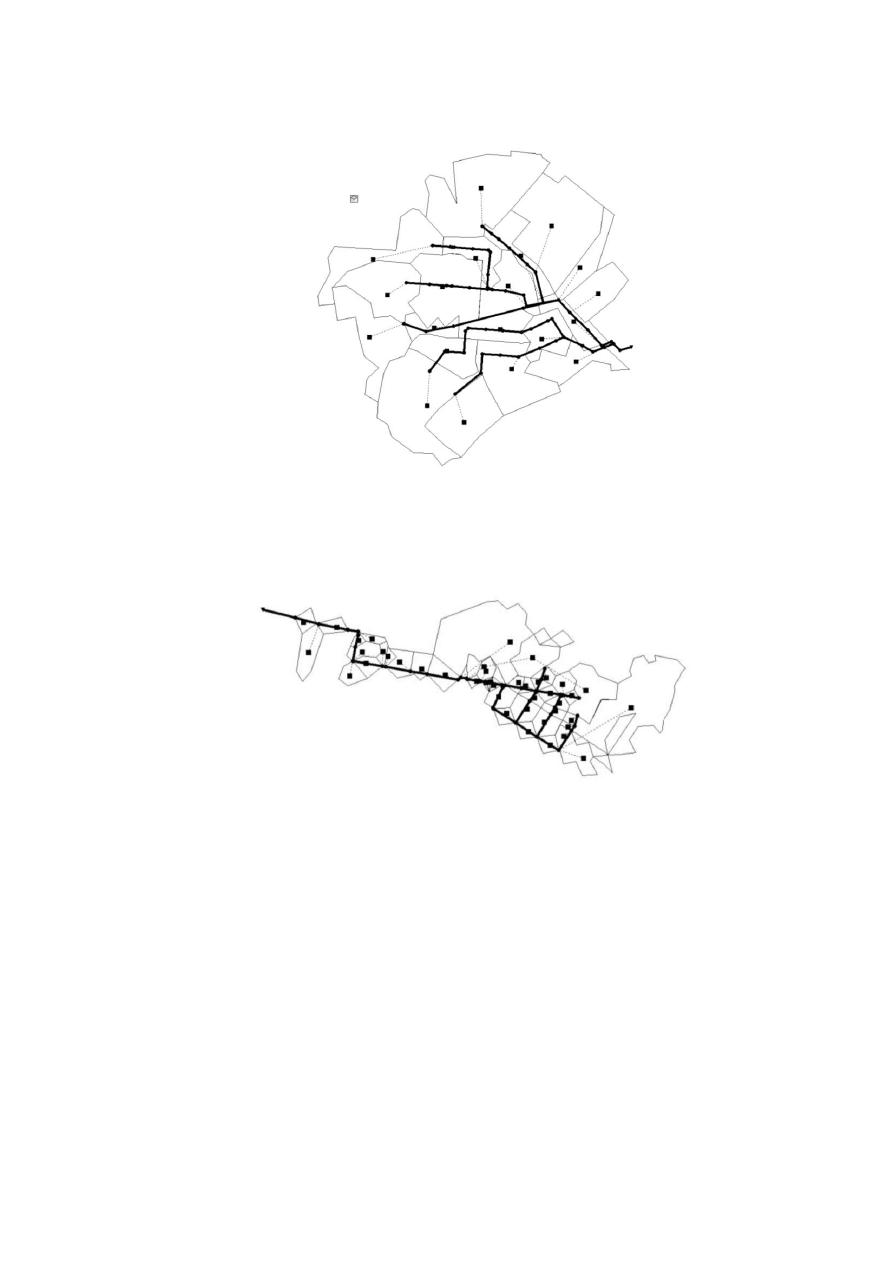
la Figura 1 se muestra el esquema de la Red Acacias.
Figura 1.- Esquema de la red Girardot-Acacias.
También se dispuso de la red Medellín-Prado, ubicada en el departamento de Antioquia-
Colombia compuesta por 50 nudos de captación y 43 subcuencas (vera Figura 2). Para el análisis de
sensibilidad se hizo uso de otros dos modelos no descritos en este documento.
Figura 2.- Esquema de la red Medellín-Prado.
Calibración con AG
Para realizar la calibración de las redes de alcantarillado utilizando AG, se hizo uso del
programa GANetXL (Centre for Water Systems, 2006) desarrollado por la Universidad de Exeter –
UK (Savic, 2010). Este programa es un complemento de Excel que permite resolver problemas de
optimización mediante el uso de AG de forma rápida y sencilla. Adicionalmente, se decidió utilizar
EPASWMM (U.S. EPA, 2010) como programa de simulación hidráulica, dada su facilidad de
acceso y la posibilidad de acoplar su motor de cálculo a programas como MS-EXCEL con VBA
para aplicaciones.
De esta manera se acopló GANetXL con EPASWMM a través de EXCEL, permitiendo una
automatización del procedimiento de optimización. Este procedimiento consiste tomar cada
individuo (una posible configuración de valores de los parámetros calibrables) de la generación
actual, mediante el uso de las funciones disponibles en GANetXL de manera que se modifica el
archivo de entrada del modelo en EPASWMM a fin de que pueda ejecutarse la hidráulica del
individuo generado y se pueda proceder a evaluar la función objetivo, y así almacenarla en
GANetXL para que genere las correspondientes mutaciones de la siguiente generación.

Haciendo uso del programa desarrollado, se realizaron diferentes procedimientos de
calibración bajo diferentes escenarios buscando recomendaciones para futuras calibraciones. Este
procedimiento se realizó para las dos redes de alcantarillado descritas anteriormente (Girardot-
Acacias y Medellín-Prado).
RESULTADOS
Los resultados de la aplicación de la metodología se muestran en dos secciones; primero se
presenta el análisis de sensibilidad del comportamiento hidráulico de redes de alcantarillado con
cambios en las propiedades físicas de las tuberías y con base en los resultados del análisis de las
redes estudiadas, se propone la metodología de calibración de las redes de alcantarillado y se
presentan algunos resultados alcanzados en los casos de estudio.
Análisis de sensibilidad
Los resultados de la sensibilidad de la respuesta hidráulica de los sistemas de drenaje urbano
se resumen en la Tabla 1. De la sensibilidad respecto a la rugosidad, se encontró que los
hidrogramas no presentan una sensibilidad suficiente para permitir el proceso de calibración
mediante mediciones de caudal. Sin embargo los limnigramas presentan una sensibilidad
considerable que se acentúa en los máximos y mínimos locales de dichas series de tiempo,
indicando así que la rugosidad puede ser un buen parámetro calibrable del sistema (ver Figura 3).
Tabla 1.- Resultados cualitativos del análisis de sensibilidad.
Rugosidad “n”
[s/m
1/3
]
Diámetro
[m]
Pendient
e [m/m]
Hidrogramas
Baja
Muy baja
Media
Limnigramas
Alta
Muy baja
Alta
Con relación a los resultados referentes al diámetro, se observó que ni los hidrogramas ni los
limnigramas son significativamente sensibles a variaciones del diámetro siempre que se asegure que
la tubería no se presuriza en ningún instante de tiempo (ver Figura 3). En el momento en que se
presuriza la tubería, el modelo presenta una sensibilidad de los hidrogramas bastante alta durante el
periodo de presurización así como una sensibilidad media en los limnigramas en los periodos de
tiempo siguientes a la presurización de la tubería. Sin embargo, del fenómeno de sobrecarga de
tuberías de alcantarillado no se tiene suficiente información para suponer que dichos resultados
corresponden acertadamente con la realidad, y por lo tanto el diámetro no constituye un buen
parámetro calibrable de los sistemas de alcantarillado.
Finalmente, se encontró que variaciones en la pendiente, pueden generar algunas variaciones
considerables en los hidrogramas así como variaciones importantes en los limnigramas. Sin
embargo el resultado más importante respecto a la pendiente, fue la conclusión de que la
sensibilidad de la respuesta hidráulica aumenta para flujos con números de Froude inferiores a 0.7
(flujos subcríticos), mientras que para flujos con números de Froude mayores a 1.0 (flujos críticos y
supercríticos) la sensibilidad decrece.
En la Figura 3 se muestra un ejemplo de los resultados encontrados en el análisis de
sensibilidad para modificaciones en el diámetro y en la rugosidad. En dicha figura, la notación
seleccionada asigna a cada escenario una combinación de tres caracteres (A, B, C) donde A
corresponde con la modificación hecha a la pendiente, B, con la modificación hecha al diámetro y
C, con la modificación hecha a la rugosidad. El valor de A, B y C es entonces: 1 si se dejó el valor
original del parámetro, 2 si se aumentó en un cierto porcentaje y 3 si se aminoró. A partir de los
resultados mostrados en dicha figura, y en otras similares no mostradas en este documento, es claro
que la rugosidad de la tubería genera cambios en la respuesta hidráulica más considerables que el
diámetro y por lo tanto es más recomendable como parámetro calibrable (si bien la modificación

relativa en el parámetro de rugosidad fue mayor que la modificación relativa en el diámetro, se
considera más probable una mala estimación a priori en el valor de la rugosidad de una tubería que
una mala estimación a priori en el valor del diámetro de la misma; y similarmente, se espera que el
error en dicha estimación de la rugosidad sea mayor que el error en la estimación del diámetro).
Figura 3.- Ejemplo de los resultados obtenidos en el análisis de sensibilidad.
Por otro lado, el análisis de sensibilidad permitió identificar que las variaciones en pocas
tuberías (una, dos o tres) sólo generan cambios en la respuesta hidráulica de nodos relativamente
cercanos a dichas tuberías. Esto indica que la calibración de sistemas de alcantarillado debe agrupar
tuberías para que el ajuste de los parámetros calibrables realizado en el procedimiento, genere
variaciones considerables en la respuesta hidráulica, y de esta manera se ajusten los resultados del
modelo con las mediciones hechas en el prototipo.
Del análisis de sensibilidad se encontró, además, que la medición de los limnigramas es
considerablemente más eficiente que la medición de los hidrogramas, dado que los niveles de la
lámina de agua son mucho más sensibles a modificaciones en el diámetro, la rugosidad y/o la
pendiente (como se puede ver en la Tabla 1).
Calibración con AG
De acuerdo con los resultados del Análisis de Sensibilidad, se definió como parámetro
calibrable, la rugosidad únicamente, teniendo en cuenta que cambios importantes en la pendiente
son menos probables en un sistema de alcantarillado, y que modificaciones en el diámetro, no
generan cambios importantes en los hidrogramas o limnigramas de la red. Además se definió como
respuesta hidráulica a comparar los limnigramas en los nodos, teniendo en cuenta que los
hidrogramas no presentan una sensibilidad suficiente. Finalmente, se decidió agrupar las tuberías de
acuerdo con su diámetro, para tener en cuenta que la respuesta hidráulica sólo varía
significativamente cuando varias tuberías son modificadas.
Utilizando la anterior información se encontró que la configuración del método de AG que
optimiza el uso del tiempo y que presenta resultados aceptables para el proceso de calibración es de
50 individuos y 100 generaciones, obtenido mediante un procedimiento de ejecuciones del
algoritmo para diferentes redes y con diferentes valores de dichas variables.
Para las ejecuciones iniciales del procedimiento de calibración, se tomaron los siguientes
valores iniciales de las demás variables del procedimiento de AG: a) Método de selección: Torneo,
b) Método de combinación: Uniforme, c) Método de mutación: Simple por gen y d) Función
objetivo (F.O.): Error cuadrático medio de la serie de tiempo de un punto seleccionado para ello.
El algoritmo fue implementado en un total de 5 redes de alcantarillado, dos de las cuales son
las redes reales descritas anteriormente (Red Girardot-Acacias y Red Medellín-Prado), otras dos
redes son basadas en redes reales, pero modificadas a fin de tener características hidráulicas
diferentes a las redes ya analizadas (Red Medellín-Prado Muy Pendiente y Red Medellín-Prado
Plano) y finalmente una red ficticia (Sistema colector).
La Tabla 2 muestra un ejemplo de los resultados alcanzados con el anterior procedimiento
para la red Girardot-Acacias. Se debe notar que cada fila de la tabla corresponde a un modelo
calibrado diferente. Ello debido a que esta metodología permite calcular diferentes configuraciones
de parámetros (una para cada punto de medición que es seleccionado para evaluar la función
objetivo), y por lo tanto se tiene una matriz de errores alcanzados. Como ventaja de la metodología
se tiene que ésta permite estimar intervalos de confianza para cada parámetro calibrable, dado que
se dispone de tantos valores de cada uno, como puntos de medición hayan sido utilizados en la
función objetivo.
Tabla 2.- Error Cuadrático Medio (ECM) entre las series de tiempo de nivel medidas y simuladas para cada
modelo generado después de la calibración de la red Girardot-Acacias utilizando diferente F.O.
Punto de evaluación
de la F.O.
ECM – Nivel (mm)
T17
T30
T32
T73
T174
Punto de
vertimiento
(outfall o salida)
T17
4.17
7.75
4.25
5.40
4.47
20.08
T30
17.25
4.28
18.85
13.22
11.86
17.32
T32
39.29
36.69
6.07
11.37
28.09
18.65
T73
32.40
60.58
23.77
6.17
47.70
3.33
T174
31.95
36.04
12.87
5.84
3.92
6.53
Punto de vertimiento
(outfall o salida)
37.29
34.79
5.77
10.74
26.63
17.64
Los resultados de la metodología con los anteriores valores de configuración de los AG y las
anteriores redes, presentaron ajustes bastante buenos para la mayoría de los limnigramas del nudo
seleccionado para evaluar la función objetivo (valores en la diagonal resaltada de la Tabla 2), pero
con errores significativos en otros nudos de medición (e.g. para el caso en donde la F.O. fue
evaluada con el nudo T73 de la red Girardot-Acacias, el error cuadrático medio en la serie del nudo
T30 fue un orden de magnitud mayor que el del nudo T73). Así, se consideró conveniente, ajustar la
función objetivo, para que incluyera todas las mediciones en todos los nudos de medición en un
único valor. Para ello se definió la nueva función objetivo como:
∑
[
[∑
[ ̂
( )
( )
]
]
|
|
]
⁄
[2]
donde,
̂
( )
es la estimación del nivel del flujo en el punto
en el tiempo hecha con la
ejecución del modelo,
( )
es la medición hecha en el prototipo del nivel del flujo en el
punto
en el tiempo ,
es la serie de tiempo de medición de la profundidad en el punto
, |
|
es la cardinalidad de dicha serie, es decir el número de instantes incluidos en la serie de tiempo, y
es el número de puntos de medición con que se dispone. Así la nueva función objetivo es el
promedio del error cuadrático medio de la serie de tiempo de cada punto de medición, y ésta logra
incluir todas las diferencias entre lo medido y lo simulado.
En la Figura 4 se muestran los resultandos alcanzados utilizando la F.O. de la Ecuación 2
para la red Girardot-Acacias con los mismos puntos de medición descritos en la Tabla 2 y la Tabla
3. Los resultados numéricos para este caso de estudio pueden ser comparados observando la Tabla 2
con la función objetivo de un único nudo y la Tabla 3 con la función objetivo que promedia los
ECM de las series de los puntos de medición. Al realizar la comparación se nota una reducción en
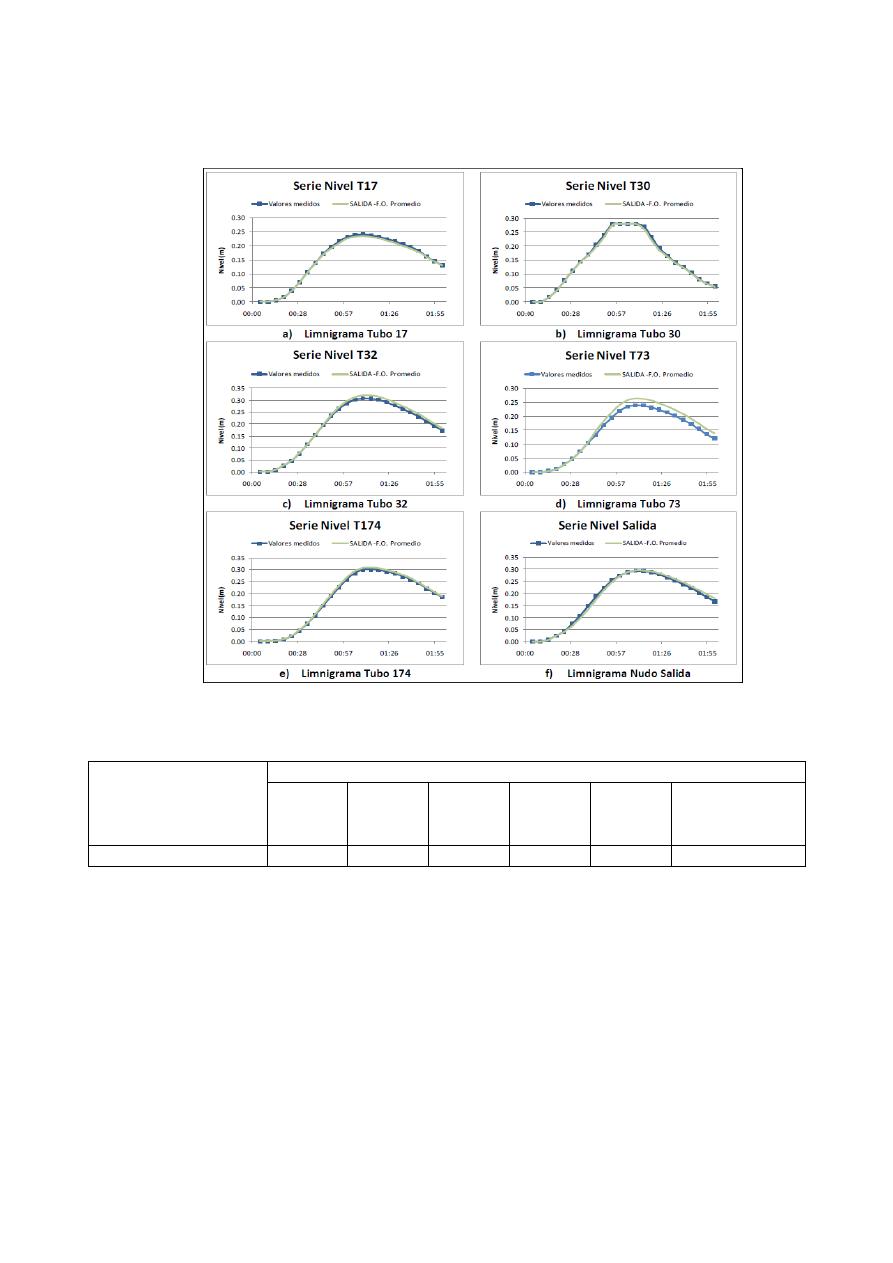
el máximo ECM de las series, indicando así que la nueva F.O. genera resultados que se ajustan
mejor a todos los puntos de medición pero sacrificando la posibilidad de generar varios modelos en
los cuales comparar los valores finales de los parámetros calibrables.
Figura 4.- Ejemplo de los resultados obtenidos en el proceso de calibración con la F.O. de la Ecuación 2.
Tabla 3.- Error Cuadrático Medio (ECM) entre las series de tiempo de nivel medidas y simuladas para el
modelo generado después de la calibración de la red Girardot-Acacias utilizando la F.O. de la Ecuación 2.
F.O.
ECM – Nivel (mm)
T17
T30
T32
T73
T174
Punto de
vertimiento
(outfall o salida)
Ecuación [2]
4.18
3.70
8.22
16.56
5.08
4.35
Es importante anotar que, dado que la calibración no se hizo con base en mediciones en el
prototipo, sino en un modelo de la red con rugosidades afectadas
(
), es posible comparar
las rugosidades encontradas por el proceso de calibración con las del modelo
a fin de
encontrar el error real en el que se está incurriendo al tomar ese resultado de la calibración como
resultado final. Como resultado de dicha comparación se encontró que los resultados de la
calibración con la F.O. de la Ecuación 2 tuvieron, para la red Girardot-Acacias, un error máximo en
el valor de la rugosidad (
de Gauckler-Manning) de 0.0027, lo que en su caso representa un error
relativo de 16% respecto a la rugosidad de
. Si bien dicho valor puede parecer un poco
alto, el error relativo promedio para todas las tuberías fue inferior a 12%, lo cual se considera
aceptable para este tipo de modelos.

Los resultados finales del proceso de calibración para todas las redes analizadas, con la F.O.
de la Ecuación 2, se muestran en la Tabla 4. Al analizar los resultados se notan los pequeños errores
alcanzados para las redes basadas en la geometría de Medellín-Prado. Ello puede deberse
precisamente a la geometría de la red, que en el caso de Medellín-Prado es considerablemente más
lineal que en Girardot-Acacias, (y que Sistema Colector), y por lo tanto ajustes en tubos aguas
arriba modifican la hidráulica de casi toda la red, y no sólo de una pequeña porción de ella como en
el caso de una red muy ramificada.
Tabla 4.- Error Cuadrático Medio (ECM) entre las series de tiempo de nivel medidas y simuladas para ellos
modelos generados después de la calibración de cada red utilizando la F.O. de la Ecuación 2.
Red
ECM – Nivel (mm)
Punto de
medición
1
Punto de
medición
2
Punto de
medición
3
Punto de
medición
4
Punto de
medición
5
Punto de
vertimiento
(outfall o salida)
Girardot-Acacias
4.18
3.70
8.22
16.56
5.08
4.35
Medellín-Prado
(Muy pendiente)
0.41
0.14
0.29
0.15
0.04
0.11
Medellín-Prado
(Pendiente)
0.06
0.40
0.01
0.03
0.02
0.58
Medellín-Prado
(Plano)
0.18
0.77
0.55
0.69
0.53
0.27
Sistema Colector
5.72
0.63
0.11
2.82
0.15
5.85
Finalmente se realizó un análisis del efecto de la ubicación de los puntos de medición en los
resultados finales del proceso de calibración (problema comúnmente conocido como sampling
design) y se llegó a la conclusión de que la ubicación de los puntos de medición no afecta
considerablemente los resultados del proceso de calibración, aunque para representar la hidráulica
de toda la red de manera ajustada sí se recomienda una distribución espacialmente homogénea de
los puntos de medición.
COLCUSIONES Y RECOMENDACIONES
En la presente investigación, se formuló y validó una metodología útil para la calibración
hidráulica de redes de alcantarillado, haciendo uso de la optimización con técnicas metaheurísticas
como lo son los AG. Este objetivo se alcanzó mediante el análisis del comportamiento hidráulico de
las redes de alcantarillado y sus cambios en la respuesta hidráulica a cambios en las propiedades
físicas de las redes.
También se logró desarrollar una herramienta sencilla y fácil de usar, que permite realizar la
calibración hidráulica de redes de alcantarillado, independientemente de sus características
topológicas, topográficas e hidráulicas. Esta herramienta hace uso del software EPASWMM en
conjunto con GANetXL (de la Universidad de Exeter) todo vinculado en un libro de EXCEL.
A partir de los resultados del análisis de sensibilidad, se concluye que el parámetro más
importante en la calibración hidráulica de las redes de alcantarillado es la rugosidad de las tuberías.
La rugosidad, en este estudio analizada como el valor de
de Gauckler-Manning, tiene un mayor
efecto en la respuesta hidráulica de la red, con un mayor efecto en las variaciones en el pico de nivel
alcanzado dentro de las tuberías. La variación de diámetros se espera que sea más importante en la
calibración de parámetros hidrológicos de la red, como el coeficiente de escorrentía, por lo que
también se esperan mayores variaciones en los picos y amplitudes de los hidrogramas.
Así mismo las mediciones en el prototipo deben incluir limnigramas en diferentes nudos de
la red, dado que este dato de salida es el más sensible a las modificaciones que se le hagan al
modelo. Con estas series se recomienda medir el error del modelo con respecto al prototipo
Por otro lado, el proceso de calibración probó ser muy sencillo y flexible. El calibrador,
siguiendo su criterio, puede variar desde la función objetivo de los AG hasta el parámetro que se

desea calibrar. En esta investigación se utiliza una función objetivo que evalúa de forma simultánea
los errores cuadráticos medios de los diferentes puntos de muestreo. Este tipo de funciones objetivo
se recomienda para realizar la calibración, ya que en la optimización con AG se selecciona la mejor
configuración de parámetros calibrables para todos los grupos de tuberías, y no la mejor para un
solo grupo de tuberías.
En cuanto a la selección de la ubicación de los puntos de medición, se concluye que los
puntos de muestreo se pueden ubicar prácticamente en cualquier sitio de la red, y los resultados que
evalúan el desempeño de la metodología de calibración no se verán afectados significativamente.
Por supuesto, es recomendable, dentro de lo posible, ubicar estos puntos de muestreo distribuidos
en toda la extensión de la red para minimizar la incertidumbre de los resultados.
Finalmente, se observó que con un total de 50 generaciones y 100 individuos en el uso de
los AG se alcanzan resultados de calidad muy similar a los alcanzados para un total de 100
generaciones y 200 individuos. Con esto se puede afirmar que no se requiere de un número muy
alto de iteraciones para lograr resultados de muy alta calidad, lo que hace más eficiente, por tiempo
y esfuerzo computacional, el proceso de la calibración hidráulica de las redes de alcantarillado.
REFERENCIAS
Centre for Water Systems – University of Exeter (2006). GANetXL Versión 1.0.4.0.
Mays, L. (2001). “Stormwater colection systems design handbook.” McGraw Hill.
Orozco, A.M. (2005). “Metodología para la calibración de modelos hidráulicos de alcantarillado”.
Magíster Tesis, Universidad de los Andes.
Savic, D. A. (2010). “GANetXL: A DSS Generator for Multiobjective Optimization of
Spreadsheet-Based Models.” Environmental Modelling and Software .
Savic, D. A., Kapelan, Z. & Jonkergouw, M.R. (2009) “Quo vadis wáter distribution model
calibraction?” Urban Water Journal, Vol 6. No 1, 3-22.
U.S. Environmental Protection Agency. (3 de Octubre de 2010). “Storm Water Management
Model.” Recuperado el Diciembre de 2010, de Urban Watershed Management Research:
http://www.epa.gov/ednnrmrl/models/swmm/
