
CÁLCULO DEL LÍMITE POBLACIONAL PARA TRATAR EL DISEÑO DE
UNA RED INTERNA COMO EL DISEÑO DE UNA RED DE DISTRIBUCIÓN
“XII Simposio Iberoamericano sobre planificación de sistemas de
abastecimiento y drenaje”
Juan Saldarriaga (1), Diego Páez (2), Daniel Vallejo (3), Santiago Serrano (4)
(1) Profesor Titular, Centro de Investigaciones en Acueductos y Alcantarillados de la Universidad de
los Andes (CIACUA), Carrera 1 No. 18ª-10, Bogotá, Colombia. Email: jsaldarr@uniandes.edu.co.
Teléfono: 3394949 Ext:2810.
(2) Profesor Instructor, Centro de Investigaciones en Acueductos y Alcantarillados de la Universidad
de los Andes (CIACUA), Carrera 1 No. 18ª-10, Bogotá, Colombia. Email:da.paez27@uniandes.edu.co.
Teléfono: 3394949 Ext: 2810.
(3) Investigador, Centro de Investigaciones en Acueductos y Alcantarillados de la Universidad de los
Andes (CIACUA), Carrera 1 No. 18ª-10, Bogotá, Colombia. Email: d.vallejo49@uniandes.edu.co,
Teléfono: 3394949 Ext: 2810.
(4) Investigador, Centro de Investigaciones en Acueductos y Alcantarillados de la Universidad de los
Andes (CIACUA), Carrera 1 No. 18ª-10, Bogotá, Colombia. Email: s.serrano1657@uniandes.edu.co ,
Teléfono: 3143721444.
RESUMEN
Las ciudades pequeñas o campamentos provisionales pueden llegar a tener poblaciones de más 5.000
personas y por esto se requiere que las redes de distribución de agua potable funcionen de manera correcta.
Para el correcto funcionamiento de estas redes se requiere de buenos diseños previos, sin embargo estos
diseños tienen algunas dificultades. En las normas vigentes no hay claridad si estas redes se deben diseñar
con metodologías de redes externas o de redes internas. Este artículo presenta una nueva metodología para el
diseño de redes internas y el cálculo del límite poblacional para el cual esta metodología es válida.
Palabras claves: Red de Distribución de Agua Potable, Red Interna de Distribución de Agua Potable, límite
poblacional.
ABSTRACT
Small cities or provisional camp sites’ population can go beyond 5.000 persons and it is why the water
distribution systems are a subject of momentous importance. There is no clarity in nowadays normativity
whether these networks should be design as Water Distribution Systems or as Plumbing Systems. This paper
presents a new methodology for designing Plumbing Systems and the calculation of the population limit for
which this methodology has a valid application.
Key words: Water Distribution System, Plumbing System, Population Limit.
SOBRE EL AUTOR PRINCIPAL
Juan Guillermo Saldarriaga: Profesor Titular de la Facultad de Ingeniería de la Universidad de los Andes.
Área de Recursos Hidráulicos, Departamento de Ingeniería Civil y Ambiental. Coordinador del Centro de
Investigación Estratégica del Agua (CIE-AGUA) de la Facultad de Ingeniería de la Universidad de los
Andes. Director del Centro de Investigaciones en Acueductos y Alcantarillados CIACUA del Departamento
de Ingeniería Civil y Ambiental de la Universidad de los Andes.

INTRODUCCIÓN
Para poder diseñar una red de distribución de agua
potable (RDAP) o una red interna de distribución de
agua potable (RIDAPS) se requieren hacer
diferentes suposiciones lo que implica que cada tipo
de red tenga su propia metodología de diseño. Tanto
la metodología de diseño para RDAP como para
RIDAPS ha evolucionado mucho; sin embargo no
está muy claro para que tamaño de ciudades, o
poblaciones, se debe utilizar cuál de las dos
metodologías.
En este trabajo se dará una breve explicación de la
nueva metodología utilizada para el diseño de las
RIDAPS y se calculará el límite poblacional para el
cual se debe pasar de diseñar como RIDAP a diseñar
como RDAP.
Para encontrar este límite poblacional en primer
lugar se tomaron ciertas redes y se diseñaron por
medio del programa REDES (programa desarrollado
por el Centro de Investigación en Acueductos y
Alcantarillados de la Universidad de los Andes,
CIACUA) para diferentes caudales demandados es
decir para diferentes poblaciones. Este programa
diseña las redes baja metodologías de RDAP. Una
vez obtenido el diseño ideal, diámetro ideal para
cada una de las tuberías, se calculó una ecuación que
lograra relacionar el número de habitantes con el
costo de la red. Después de esto se procedió a
diseñar la red por metodologías de RIDAPS. Para
este proceso se utilizó el programa DisRed
(programa desarrollado por CIACUA). Una vez
obtenida la red óptima y su costo se procedió a
encontrar la población a la cual se igualaban estos
costos; esta se denomina la población de equilibrio.
MARCO TEÓRICO
Los procesos de diseño de una RDAP y una RIDAP
están gobernados por los mismos principios físicos.
Sin embargo las metodologías de diseño difieren,
especialmente cuando se trata de determinar las
presiones mínimas y los caudales de diseño.
Presiones mínimas en un RDAP
Las presiones mínimas para las RDAP están
establecidas en las normas de cada país. En el caso
de Colombia estas se encuentran en el Reglamento
Técnico del Sector de Agua Potable y Saneamiento
Básico (RAS). Estas presiones mínimas se presentan
en la Tabla 1.
Tabla 1. Presiones mínimas en las RDAP
según el RAS 2000.
Nivel de
Complejidad
del Sistema
Población en la
zona urbana
Presión
Mínima en la
red (m)
Bajo
<2,500
10
Medio
2,501 a 12,500
10
Medio Alto
12,501 a 60,000
15
Alto
>60,000
15
Estimación de la demandas en RDAP
El RAS presenta tres metodologías para la
determinación del caudal demandado en una red. El
método de las áreas, el método de la carga unitaria y
el método de la repartición media. El método de la
carga unitaria fue el utilizado durante todo el
proceso y por eso es el que se describe. Este método
se basa en determinar la cantidad de agua
demandada por usuario en un instante del tiempo. El
RAS establece la siguiente tabla para la dotación
neta.
Tabla 2. Dotación por habitante según el
nivel de complejidad del sistema.
Nivel de
complejidad
del sistema
Dotación neta
(L/hab·día )
Clima Templado
y Frío
Dotación neta
(L/hab·día )
Clima Cálido
Bajo
90
100
Medio
115
125
Medio Alto
125
135
Alto
140
150
Estas dotaciones netas deben ser mayoradas para así
tener en cuenta las pérdidas; a continuación se
presentan los porcentajes que conciernen a las redes
de distribución
Tabla 3. Porcentajes de pérdidas por
componente.
Red de Distribución
Nivel de Complejidad Bajo
27%
Nivel de Complejidad Medio
24%
Nivel de Complejidad Medio Alto
19%
Nivel de Complejidad Alto
19%
(1)
Una vez se tiene la demanda bruta se procede a
calcular el caudal máximo horario
.
Tabla 4. Estimación de la demanda según
RAS 2000.
Caudal
Definición
Ecuación
Medio Diario
(Qmd)
Promedio de los
consumo diarios
en un periodo
de un año
Máximo Diario
(QMD)
Máximo
registrado en un
día durante un
periodo de un
año
Máximo
Horario
(QMH)
Máximo
registrado
durante una
hora en un
periodo de un
año
Para determinar los valores de k1 y k2 se debe
utilizar la siguiente tabla.
Tabla 5. Valores de k
1
y k
2
.
Nivel de
Complejidad
del Sistema
Coeficiente de
consumo
máximo diario
k1
Coeficiente de consumo
máximo horario k2
Red
Menor
Red
Secundaria
Red
Matriz
Bajo
1.3
1.6
-
-
Medio
1.3
1.6
1.5
-
Medio Alto
1.2
1.5
1.45
1.4
Alto
1.2
1.5
1.45
1.4
Estimación de las presiones y demandas en
RIDAP
La determinación de las presiones y los caudales de
diseño van muy de la mano cuando se trata de
diseñar una red interna.
El diseño de una RIDAP se basa en conocer el
comportamiento de cada nudo de consumo; esto
implica conocer qué tipo de emisor, o aparato, se
encuentra allí conectado y cómo se comporta. Por
emisor, o aparato, se hace referencia a los
lavamanos, inodoros, regaderas o demás utensilios
que hagan uso del agua de la red.
Ha habido una gran cantidad de metodologías
propuestas
para
este
tema.
Las
primeras
metodologías fueron método británico, método
alemán de la raíz cuadrada, método racional y el
método de hunter. Estos métodos se basaban en
tablas para calcular el caudal y las presiones en los
nudos.
Posterior a esto vinieron nuevas metodologías las
cueles se conocen como los métodos modernos.
La principal característica de estas metodologías es
que se deja de suponer que la demanda es
homogénea a lo largo del día y por esto se empieza a
trabajar con pulsos para la demanda de agua.
Basándose en el concepto de los pulsos se creó en
2011 el software RIDAP, en la Universidad de los
Andes (CIACUA, 2011). Este tenía la capacidad de
hacer diseños de RIDAPS; sin embargo tenia
algunas deficiencias (Vallejo, 2012).
En este artículo se presenta una nueva metodología y
un nuevo software capaz de diseñar una RIDAP
obteniendo mejores resultados y con menores
tiempos
computacionales
que
los
software
anteriores.
Relación caudal presión
Las RIDAP tienen emisores en casi todo el nudo de
demanda de la red, esto quiere decir que los caudales
demandados dependen de la presión. A raíz de esto
se crearon curvas que relacionaran el caudal con la
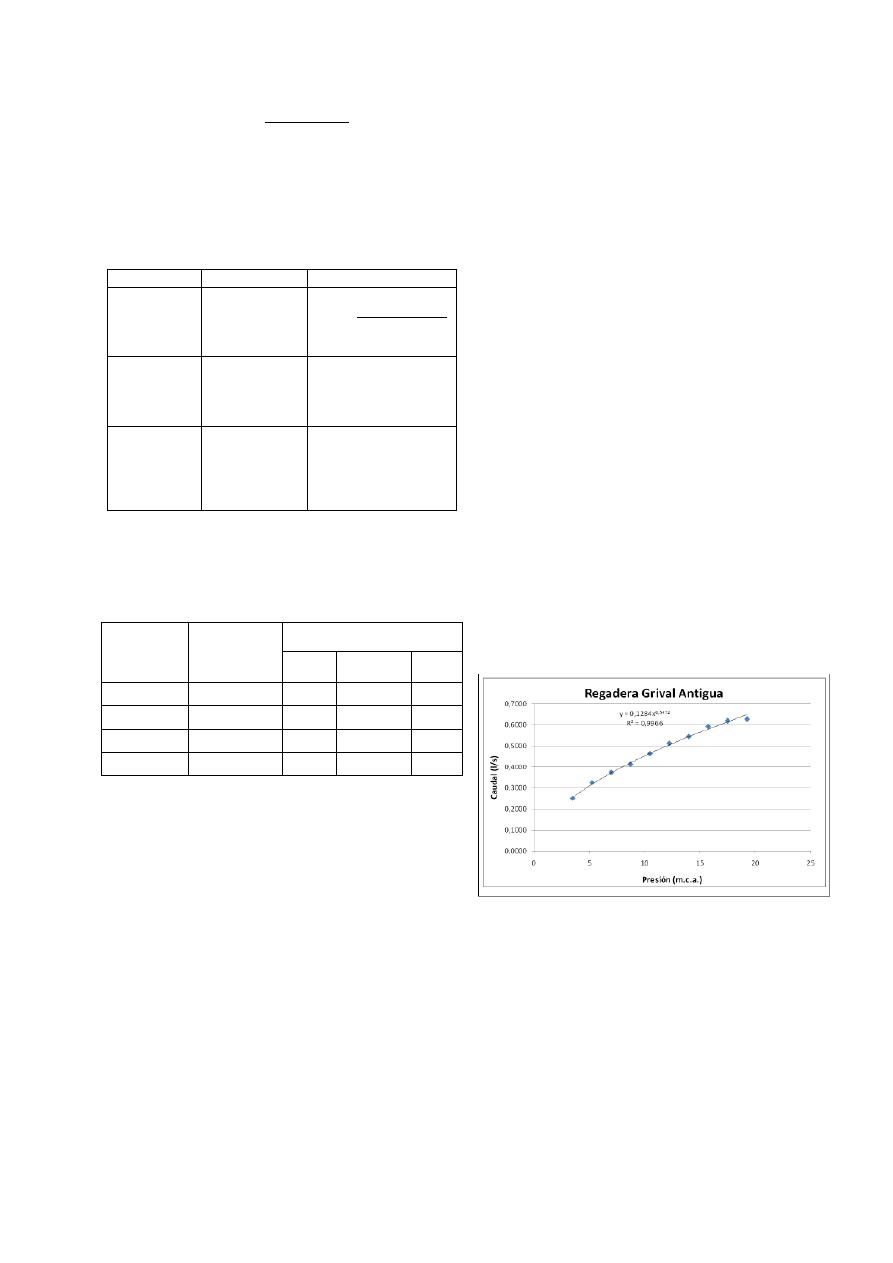
presión. (Acero, 2009). En la Gráfica 1 se presenta
la relación de caudal contra presión para una
regadera.
Gráfica 1. Curva caudal vs presión para
regadera.
NUEVA METODOLOGÍA
En su tesis de maestría en la Universidad de los
Andes, Diego Páez (Páez, 2011) propone una nueva
metodología para el diseño de las RIDAPs.
La metodología propone calcular los caudales de
diseño por medio de las curvas únicas de cada uno
de los aparatos instalados en la red. Para hacer el
cálculo de este caudal se propone definir el número

de aparatos que se encontrarán encendidos en un
determinado momento y simplemente sumar los
diferentes caudales demandados.
En primer lugar se debe determinar cuál es la
probabilidad de que un aparato se encuentre
encendido en un determinado momento del tiempo,
esto se hace por medio de un análisis de estados.
Estados
La palabra estados hace referencia al número de
aparatos aguas abajo de un nudo que se encuentran
encendidos en un momento dado. Por ejemplo un
nudo que tenga 4 aparatos aguas abajo tendría la
posibilidad de tener 4, 3, 2, 1 o ningún aparato
encendido; además de esto, para cada posibilidad
podrían ser diferentes los aparatos encendidos. Esto
quiere decir que para 4 aparatos existen 16 distintas
escenarios o estados los cuales habría que evaluar
para determinar el caudal. El cálculo de este valor se
resume en:
∑ ( )
( )
donde,
.
Si se hiciera este mismo proceso para un caso con un
estado máximo de 16, se tendrían que hacer 65.536
evaluaciones de probabilidad; esto se convierte ya en
un valor muy alto para evaluar de manera eficiente.
En (Páez, 2011) se propone utilizar la siguiente
ecuación la cual no implicaría mayor error y si
reduciría considerablemente los tiempos de cálculo.
( )
∑
(∏
∏ (
)
)
( )
donde,
.
Sin embargo no todos los aparatos tendrán la misma
probabilidad (p) de estar encendidos en un
determinado momento. Después de hacer un análisis
se determina (Páez, 2011) que la más acertada es
una ecuación de Promedio Geométrico.
( ) ( )
( )
(∏
)
( ((∏
)
(∏
(
))
))
(∏
( )
)
((∏
)
(∏
( )
)
)
(4)
El caudal de diseño se toma como como la suma de
los caudales de los N aparatos con mayor caudal, N
hace referencia al número del estado cuya
probabilidad acumulada supera la probabilidad de
falla.
Nuevo Software
Con la finalidad de poder hacer diseños de RIDAPS
con la metodología planteada se creó un software
que la implementara, el programa se conoce bajo el
nombre de DisRed, (Vallejo, 2012).
El programa desarrollado tiene una serie de
parámetros de entrada los cuales son necesarios para
poder realizar los diseños.
Topología
Para poder hacer el diseño de una red y determinar
los diámetros de las tuberías, se requiere hacer una
planeación dimensional de la res. Cuando se habla
de topología se hace referencia a la ubicación de
cada
uno
de
los
nudos
en
coordenadas
tridimensionales.
La generación de estas topologías es un proceso
sencillo y se puede hacer en el programa EPANET,
(Rossman, 2000).
Una vez se ha creado la topología solo se requiere
exportar este en el formato establecido por
EPANET, formato .INP.
Curvas de Aparatos
Para aumentar la precisión en los resultados DisRed
calcula los caudales en los nudos por medio de
curvas que relacionan las presiones con caudales.
Estas curvas son únicas para cada estilo de aparato,
(Acero, 2009).
Aunque las curvas aumentan la precisión de los
resultados, en la realidad el caudal que utiliza un
aparato no sólo depende de la presión si no de que
tan abierta está la llave reguladora de caudal, es
decir que se cuenta con distintas curvas para
diferentes niveles de apertura en la llave.
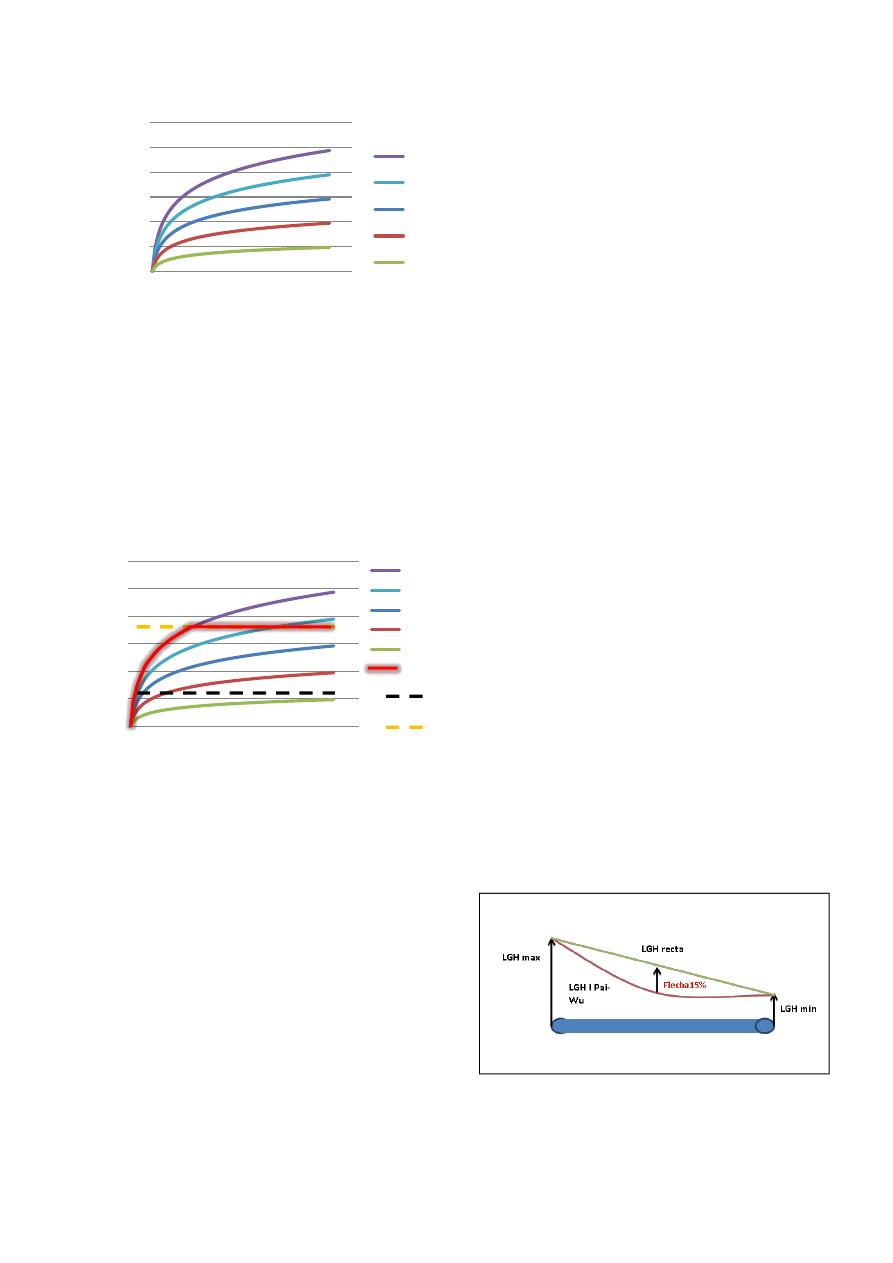
Gráfica 2. Presión vs Caudal para diferentes
aperturas.
Aunque los aparatos utilizan diferentes caudales
acorde a la necesidad del usuario estos se encuentran
dentro de ciertos rangos. Siempre se va a tener un
caudal mínimo requerido para que el aparato cumpla
con su función. También se tendrá un caudal
máximo el cual si es superado el aparato podría no
cumplir con su correcto funcionamiento. Basándose
en lo anterior se define la curva única.
Gráfica 3. Curva única.
La curva única para cada aparato es el parámetro que
se debe ingresar al programa ya que es con estas
curvas que se calculará el caudal de diseño para los
aparatos.
Parámetros
El programa requiere el ingreso de 4 parámetros
generales: la viscosidad cinemática, el exponente del
redondeo potencial, listado de los diámetros
comerciales y el valor F para el cálculo de la LGH.
Además de estos parámetros también se deben
ingresar algunos parámetros específicos para cada
estilo de aparato. El termino F se utiliza en el
momento de calcular las presiones en los nudos. Este
concepto fue introducido por I Pai Wu (Wu, 1975) y
hace parte de la Ecuación 5 la cual se explica más
adelante.
Presión mínima: se debe especificar la
presión mínima que requiere el aparato para
tener un correcto funcionamiento
.
Curva: se debe especificar que curva
corresponde a cada aparato, es decir
especificar que estilo de aparato es.
Frecuencia: para cada aparato se debe
ingresar la frecuencia de uso, las frecuencias
se deben ingresar en usos/(hora*persona).
Usuarios: se debe especificar el número de
usuarios que tienen acceso a dicho aparato.
Duración: cada aparato tiene diferentes
duraciones de usos y es por esto que se debe
definir para cada uno.
Existe una amplia bibliografía acerca de estos
valores; cabe resaltar que de la realidad de estos
parámetros depende la precisión del diseño. Para los
cálculos presentados en este informe se hizo uso de
los valores presentados en (Blocker, 2010)
Determinación del caudal de diseño
Cálculo de la LGH:
Este proceso se hace por medio de la metodología
planteada por I Pai Wu (Wu, 1975). Al usar esta
metodología se logra llegar a saber la presión
mínima que debe haber en cada uno de los nudos.
Estos cálculos se basan en la presión mínima en los
nudos de consumo (
)y la presión a la
entrada del sistema
(
). Los cálculos se
hacen con la siguiente ecuación donde L representa
la longitud hasta la fuente, F el valor de la flecha y X
la posición dentro de la tubería donde se desea
determinar el valor de LGH. Esta información e
observa con mayor claridad de la Figura 1, en este
caso el valor de F es de 15% ya que Wu define que
este es el valor óptimo, (Wu, 1975).
Figura 1. Diagrama LGH según I Pai Wu.
Ca
u
d
a
l
Presión
100%
80%
60%
40%
20%
Apertura
Cau
d
a
l
Presión
100%
80%
60%
40%
20%
Apertura
Mínimo
Máximo
Única

( )
( )
( )
Probabilidad de Uso
Para determinar el caudal de diseño, es necesario
determinar la probabilidad de que un determinado
aparato se encuentre encendido en algún momento
del día.
Una vez se han calculado las probabilidades se
procede a calcular la probabilidad de ocurrencia de
cada uno de los posibles estados para cada nudo,
incluyendo el estado 0, la suma de estas
probabilidades es 1,0.
Después de esto se procede a recalcular estas
probabilidades suponiendo que el sistema se
encuentra en uso, es decir eliminando es estado 0;
esto se hace para aumentar la realidad de los datos.
Finalmente se determina para cual estado la suma de
probabilidades supera la probabilidad de falla; este
queda definido como el número de aparatos aguas
abajo del nudo que se tomarán como encendidos.
Tabla 6. Probabilidad acumulada para
encontrar el estado de diseño. Ejemplo.
Estados
No uso
En uso
P acumulada
6
0,01
0,01
1,00
5
0,03
0,04
0,99
4
0,10
0,14
0,94
3
0,16
0,23
0,80
2
0,19
0,27
0,57
1
0,21
0,30
0,30
0
0,30
Total
1,00
1,00
Determinación del caudal
Una vez se ha determinado el estado por medio del
proceso anterior se puede calcular el caudal de
diseño. Para esto se toman los N aparatos con mayor
caudal aguas abajo del nudo que se quiere diseñar,
donde N el valor del estado encontrado.
Para el caso planteado en la Tabla 6, se tomarían los
5 aparatos de mayor caudal aguas abajo del nudo y
se les sumarian sus caudales.
Los caudales a sumar se determinan por medio de
las curvas ingresadas en un principio.
Redondeo
Una vez se calculan los caudales se procede a hacer
un proceso de diseño, como resultado de este se
obtienen los diámetros con los cuales la red
cumpliría con los caudales y presiones. Para
aumentar la precisión estos diámetros están en
formato continuo, es decir que se tienen diámetros
de cualquier valor mas no necesariamente que
existan en la realidad.
Debido a esto el programa trae diferentes opciones
de
redondeo,
Diámetros
Anterior,
Diámetro
Siguiente y Redondeo Potencial.
Después de hacer diseños para 5 diferentes redes por
medio de los 3 tipos de redondeo se observó que se
obtenían mejores resultados haciéndolo por medio
de un redondeo potencial.
METODOLOGÍA PARA EL LÍMITE
POBLACIONAL
Las ciudades pequeñas o campamentos provisionales
pueden llegar a tener poblaciones de más de 5000
personas por lo que es de gran importancia el buen
diseño de la red de distribución de agua potable.
No está claro si estas redes deben modelarse como
redes de distribución de agua potable (RDAP) o
como redes internas de distribución de agua potable
(RIDAP). Si bien sus características hidráulicas no
difieren en gran medida, los parámetros de entrada
como las presiones y los caudales sí lo hacen.
Debido a estas diferencia es que se quiere encontrar
un límite poblacional que defina bajo qué
condiciones se debe modelar la red.
Para encontrar este límite poblacional se escogieron
6 redes de ciudadelas o campamentos pequeños.
Cada una de estas redes fue diseñada por medio de
metodologías de RDAP y de RIDAP para así poder
establecer el límite poblacional.
RDAP
Para determinar el límite poblacional se empezó por
diseñar las redes por medio de metodologías de
RDAP. Estos diseños se realizaron utilizando el
software REDES (CIACUA, 2011).
Para estos diseños se utilizó el método de la carga
unitaria para determinar el caudal de diseño, esta
decisión se toma basándose en Torrado, (2012).
Para estos diseños fue necesario estimar la demanda
que tendría la red en cada uno de los nudos de
consumo.
Para determinar el caudal demandado en cada nudo
se requiere saber la dotación neta (Tabla 2), el
porcentaje de pérdidas (Tabla 3) y los valores de k
1
y k
2
(Tabla 5). Se consideró que para estas redes la
población se distribuía de manera uniforme por lo
que los usuarios por nudo estarían establecidos como
la población total dividida el número de nudos de
consumo:
( )
donde,
Para el diseño se utilizó el caudal máximo horario, el
cual está definido por las ecuaciones de la Tabla 4.
Este proceso se realizó para una serie de
poblaciones, es decir que se diseñó cada red para
diferentes poblaciones y para cada diseño se calculó
el costo de la red. Estos costos se calcularon por
medio de la siguiente ecuación:
∑
( )
donde, L y D representan la longitud y el diámetros
de la tubería i, respectivamente, y k y x son
parámetros obtenidos de la curva de costos mostrada
en la siguiente gráfica.
Gráfica 4. Curva de costos.
Haciendo una regresión lineal de los anteriores
valores se obtiene que la ecuación que los describe
es:
, de aca se consluye que
k=1.0139 y x=0.6728.
Una vez calculados los costos de las redes para cada
población se procedió encontrar la ecuación que las
describiera; después de varios análisis se encontró
que una regresión potencial era la que mejor se
adaptaba a los datos obtenidos.
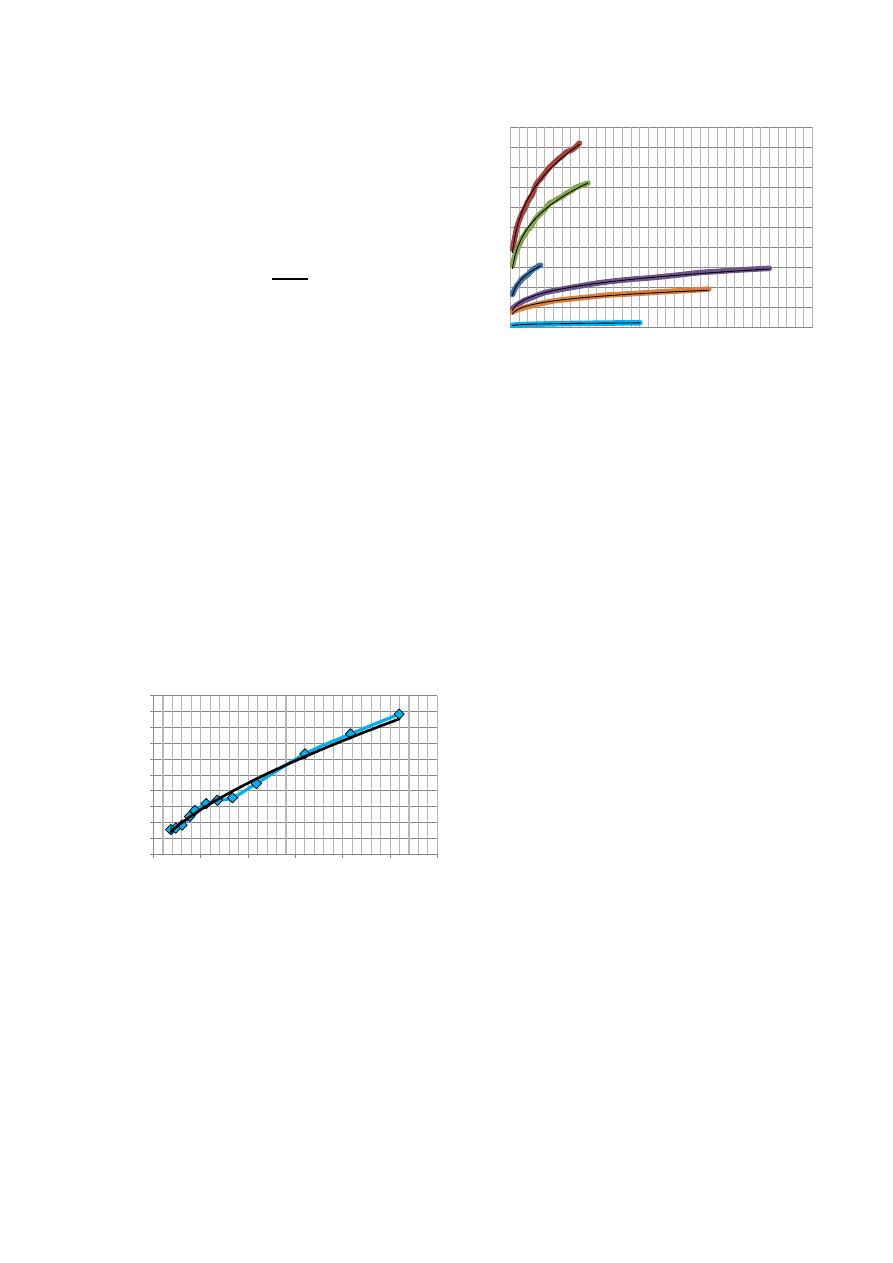
Gráfica 5. Ajuste de los diseños
poblacionales mediante una regresión
potencial.
La anterior gráfica presenta las relaciones entre
número de habitantes contra costos para cada una de
las 6 redes. Se muestra claramente que las
regresiones potenciales describen de manera
acertada las relaciones, de hecho el R
2
más bajo fue
de 0.987.
RIDAP
Para los diseños basados en metodologías de RIDAP
el procedimiento fue distinto. Para estos diseños se
utilizó el programa DisRed, descrito en este artículo,
y la metodología que este usa.
En primer lugar el método para determinar el caudal
de diseño es absolutamente distinto al método
utilizado para las RDAP. Para diseñar las redes por
medio de RIDAPS se utiliza el caudal máximo
probable, esto quiere decir que para determinar este
caudal no se utilizaran todos los nudos demandando
en un mismo instante de tiempo; se utiliza el caudal
demandado por la situación más probable.
En segundo lugar se requirió desagregar las redes.
Por desagregar se hace referencia a llevar el modelo
hasta los nudos directos de consumo y no sólo hasta
el punto de abastecimiento. El procedimiento de
desagregación
implica
unos
mayores
costos
computacionales ya que el número de nudos en la
red incrementa significativamente.
A continuación se presenta en lo que se
transformaría el nudo de consumo original. Como se
puede observar al agregar un mayor detalle a la red,
agregar cada nudo de consumo, la red aumentará su
tamaño.
0
5
10
15
20
25
30
35
40
45
50
0
50
100
150
200
250
300
CO
ST
O
(USD
)
DIÁMETRO INTERNO (mm)
C
osto
(U
S
D
)
N
Habitantes
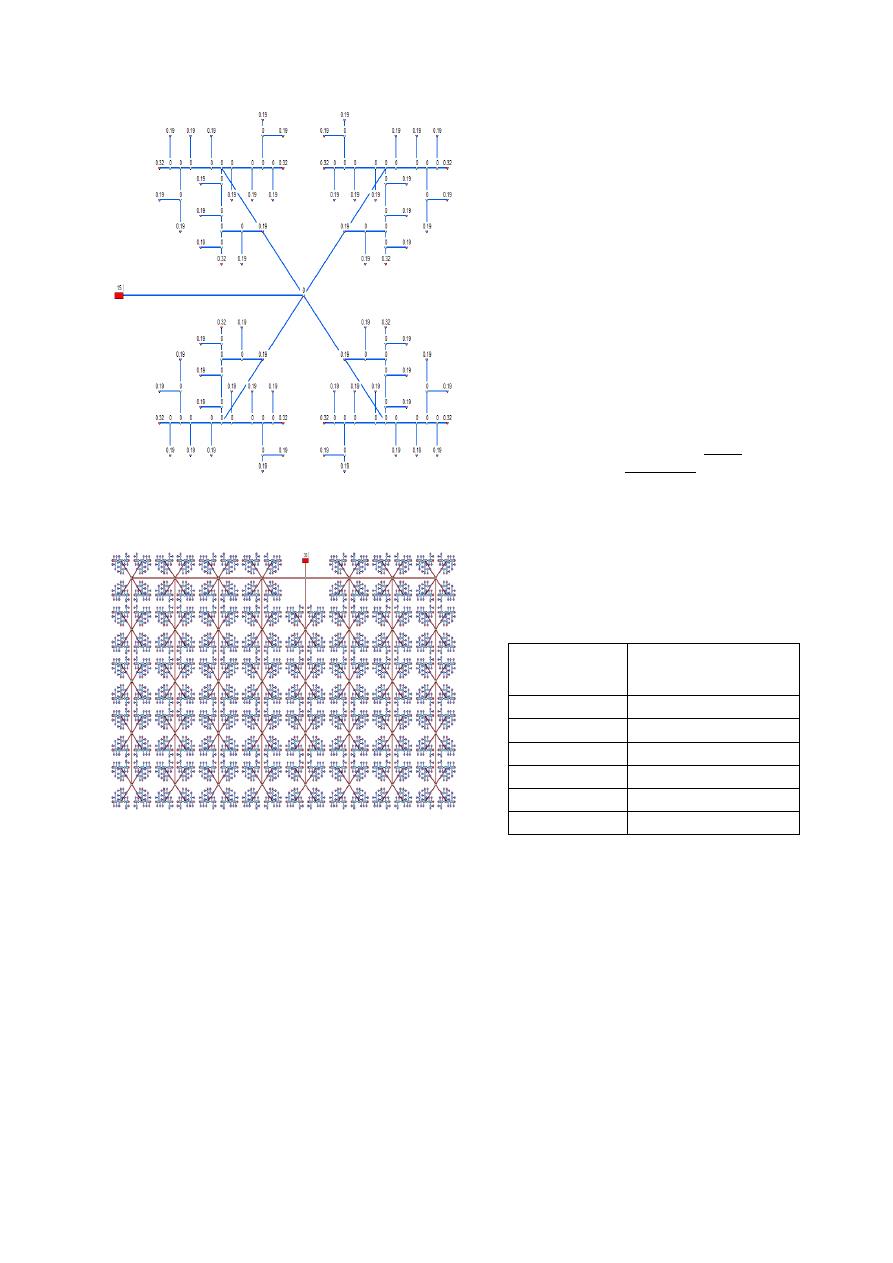
Figura 2. Esquema para RIDAP red R-28.
Después de aumentar el nivel de detalle la red
quedará representada de la siguiente manera:
Figura 3. Esquema de la red R-27 ya
desagregada.
Una vez se ha desagregado la red se procede a
asignar la presión mínima, curva de cada aparato,
frecuencia, usuarios y duración a cada nudo de
consumo. Este proceso puede ser tedioso debido al
alto número de nudos de consumo que puede llegar a
tener una de estas redes.
Una vez se completaron los diseños por medio de
metodologías RIDAP se calcularon los costos que
tendrían estas redes; cabe aclarar que estos costos se
calcularon por medio de redondeo al diámetro
anterior ya que este tipo de redondeo generaba las
tuberías con menor diámetro y por ende el menor
costo para la red.
Cálculo de población de equilibrio
Una vez se cuenta con los costos de diseño por parte
de las dos metodologías se procede a encontrar la
población de equilibrio. La población de equilibrio
es aquel número de personas que hacen que un
diseño por medio de RIDAPS iguale al costo de
RDAP.
Para determinar este valor se resuelve la ecuación
potencial, encontrada para cada una de las redes en
el diseño RDAP, igualándola al costo obtenido por
medio de metodología RIDAP.
Se presenta el caso específico de uno de las redes
escogidas.
(
)
Este mismo proceso se realizó para las otras 6 redes
y se obtuvieron las siguientes poblaciones
.
Tabla 7. Población de equilibrio bajo
regresión potencial.
Red
Población de
Equilibrio (N°
Habitantes)
Campamento 1
2,186
Campamento 2
4,425
R-28
4,487
Oasis IV
11,372
Red Elevada
6,154
San Vicente
5,896
Análisis
De la tabla 7 se observa que las 6 poblaciones de
equilibrio no son iguales. Estas diferencias tenían
que estar reflejadas en alguna característica de las
redes como el número de nudos de consumo, el
tamaño de la red o del caudal demandado.
Se realizó un análisis para poder llegar a definir la
población de equilibrio de cualquier red sin tener
que hacer todo el proceso previamente realizado.
En este proceso se encontró una relación bastante
importante:

Gráfica 6. Correlación entre la población de
equilibrio y el caudal RDAP.
Se encontró que existe una relación directa entre el
Q de diseño usado en las RDAP contra la población
de equilibrio; esta relación estaría descrita por:
(
)
Esta relación permite saber bajo que metodología se
debe diseñar cada una de las redes.
CONCLUSIONES
Después de haber diseñado un nuevo de diseño de
RIDAP y haciendo varias pruebas se puedo concluir
que el redondeo más acertado a utilizar sería un
redondeo potencial. Eso se concluye ya que es el de
costo medio pero cumple con una mayor variedad de
situaciones críticas.
Al hacer los diseños utilizando probabilidades que
partan del hecho que el sistema está en uso aumenta
la realidad y confiabilidad de los resultados.
Al poder incluir una alta cantidad de variables en el
programa se aumenta la realidad de los resultados, el
hecho de poder distinguir un lavamanos de un nudo
cualquiera hace que el diseño sea más preciso.
Se encontró que a medida que aumenta el número de
habitantes de una red el costo de esta aumenta en
menor medida, es decir que disminuye el costo por
habitante.
Se encontró que la población de equilibrio de una
red depende linealmente del caudal demandado por
medio de análisis de carga unitaria. Esta relación se
mantendrá para todo rango de caudal debido a la
relación lineal y al buen coeficiente de ajuste.
En caso de que la red tenga una población menor a
la de equilibrio esta se deberá diseñar por medio de
metodologías RIDAP, de lo contrario se debe hacer
por metodologías RDAP.
BIBLIOGRAFÍA
Acero, M. F. (2009). Revisión Crítica de los
Métodos de Diseño de Abastecimiento de
Agua Potable al Interior de Edificaciones.
Bogotá: Tesis de Maestría, Universidad de
los Andes.
Acero, M. F. (2009). Revisión Crítica de los
Métodos de Diseño de Abastecimiento de
Agua Potable al Interior de Edificaciones.
Bogotá: Tesis de Maestría, Universidad de
los Andes.
Blocker, E. (2010). Stochastic water demand
modeling for a better understanding in
hydraulics in water distribution networks.
Neatherlands: PHD Thesis, Delft University.
CIACUA. (2011). Desarrollo e implementación de
una metodología moderna para el diseño de
redes internas de distribución de agua
potable. Bogotá: Universidad de los Andes:
Colciencias.
Páez, D. A. (2011). Análisis de Redes Internas de
Distribución de Agua Potable utilizando
Simulación de Eventos Discretos. Bogotá:
Tesis maestría, Universidad de los Andes.
Rossman, L. (2000). EPANET 2 User's Manual.
Cincinati OH: Risk Reduction Engineering
Laboratory: US Enviremental Protection
Agency.
Serrano, S. (2012). Límite poblacional (ciudades
pequeñas, campamentos provicionales y
permanenstes) para el cuas se debe hacer
uso de programas de diseño de RDAP vs.
programas de diseño de RDAP. Bogotá:
Tesis pregrado, Universidad de los Andes.
Torrado, D. (2012). Comparación de moetodologías
de diseño de redes externas de distribución
de agua potable vs. Metodologías de diseño
de redes internas para el caso el caso de
campamentos
y
ciudades
temporales.
Bogotá.: Trabajo de grado especialización,
Universidad de los Andes.
Vallejo, D. (2012). Diseño e implementación del
programa DisRed para el diseño de Redes
Internas de Distribución de Agua Potable.
Bogotá: Tesis de Pregrago, Universidad de
los Andes.
Wu, I. P. (1975). Design of a drip of irrigation main
lines. ASCE: Journal of Irrigation and
Drainage Division.
0
2000
4000
6000
8000
10000
12000
0.00
10.00 20.00 30.00 40.00 50.00
P
o
b
lac
ió
n
d
e E
q
u
il
ib
ri
o
(
N
de
Ha
bit
an
tes
)
Q_RDAP

