
IAHR
CIC
XXV CONGRESO LATINOAMERICANO DE HIDRÁULICA
SAN JOSÉ, COSTA RICA, 9 AL 12 DE SETIEMBRE DE 2012
ANÁLISIS ESTADÍSTICO DE DIFERENTES AJUSTES PARA LA
MODELACIÓN DE LA CONCENTRACIÓN DE CLORO EN MODELOS
ESQUELETIZADOS DE RDAP
J.G. Saldarriaga
1
, S. García
2
, N. León
2
1
Profesor Titular, Departamento de Ingeniería Civil y Ambiental - Director, Centro de Investigación en Acueductos y Alcantarillados –CIACUA–,
Universidad de los Andes, Bogotá, Colombia; email: jsaldarr@uniandes.edu.co.
2
Investigadores, Centro de Investigación en Acueductos y Alcantarillados –CIACUA–, Departamento de Ingeniería Civil y Ambiental, Universidad
de los Andes, Bogotá, Colombia; email: n.leon40@uniandes.edu.co; sa.garcia32@uniandes.edu.co
RESUMEN:
La esqueletización de sistemas de distribución consiste en la selección y remoción de tubos de la
red, obteniendo así un modelo que represente adecuadamente las propiedades hidráulicas del
original. Las ecuaciones para la modelación de la calidad del agua son función de la velocidad. La
esqueletización afecta las velocidades modeladas en el sistema y por tanto se ve afectada la calidad
del agua. Para disminuir este impacto, el presente estudio propone una metodología que utiliza
relaciones entre el tiempo de residencia del agua y el caudal, permitiendo obtener parámetros
adimensionales que afectan la concentración de cloro y mejoran la modelación de la calidad.
Finalmente, la metodología fue aplicada a dos casos de estudio de Redes de Distribución de Agua
Potable (RDAP) obteniendo resultados satisfactorios: los parámetros adimensionales modifican el
decaimiento del cloro y los modelos esqueletizados representan de manera precisa el
comportamiento hidráulico de las redes originales.
ABSTRACT:
The skeletonization process in water distribution systems consists in selecting and removing
network pipes until the obtained model adequately represents the hydraulic qualities of the original.
Applying this process affects the system’s modeled velocities, which is why the equations cannot
represent its water quality adequately. This paper presents a methodology that uses dimensionless
parameters to preserve water quality in skeletonized models of Water Distribution Networks, or
WDN. The methodology also expresses relations between water residence time and flow to obtain
dimensionless factors. These factors alter chlorine concentrations and improve the modeling of
water quality. Finally, the methodology was applied in two WDNs and the results that were
obtained were satisfactory; the skeletonized models accurately reproduce the hydraulic behavior,
and the dimensionless parameters modify chlorine decay.
PALABRAS CLAVE:
Esqueletización, Redes de Distribución, Concentración de Cloro, Factores Adimensionales.

INTRODUCCIÓN
Los modelos esqueletizados de RDAP son generados por medio de la selección y eliminación de un
cierto número de tubos y nudos, de tal manera que el nuevo modelo logre reproducir de manera
adecuada la hidráulica del prototipo. Dichos modelos esqueletizados son de gran utilidad, e incluso
necesarios, en términos de operación de una red. Tienen aplicaciones como por ejemplo manejo en
tiempo real, monitoreo de la calidad del agua, coordinación de operaciones de mantenimiento, y
atención de emergencias, debido a que reducen en gran medida el número de cálculos. El propósito
de este artículo es presentar una nueva metodología de esqueletización que no afecta de manera
considerable los resultados de calidad del agua en el modelo reducido.
La metodología propuesta se divide en dos etapas. La primera es la etapa de esqueletización. Ésta
consta de cuatro pasos. Primero, se realiza un proceso de agregación de demandas que busca
concentrar varios nudos de baja demanda en un único punto. Luego, se aplica una metodología
tradicional de esqueletización, utilizando el concepto de Potencia Unitaria (PU) para seleccionar los
tubos a remover en cada iteración. Cuando no es posible remover más tubos, se eliminan los nudos
con demanda cero y que no tengan dependencias aguas abajo. Finalmente, algunas de las series de
tubos en el sistema son remplazadas por tuberías simples, las cuales producen pérdidas equivalentes
a las producidas por la serie original. Esto se realiza únicamente para tuberías en serie que incluyen
nudos con demanda nula. La segunda etapa busca preservar la equivalencia en la calidad, con
respecto al prototipo. Para este fin se modifican las ecuaciones de decaimiento del cloro para cada
tubo de manera individual, usando una serie de relaciones entre el caudal original y el del modelo
esqueletizado. Estas relaciones son obtenidas por medio del uso de parámetros adimensionales
derivados de las ecuaciones de decaimiento de primer orden que caracterizan al cloro en las RDAP.
La metodología fue puesta a prueba en sistemas de distribución reales, permitiendo obtener una
considerable reducción en la topología de los mismos y a la vez una adecuada modelación de la
calidad del agua. Por otra parte, las simulaciones de calidad del agua realizadas sobre el modelo
esqueletizado, evidenciaron un aumento en la correspondencia entre éste y el modelo original, en
comparación con la correspondencia obtenida al aplicar otras aproximaciones.
MARCO TEÓRICO
Para el desarrollo de este artículo es importante entender los efectos de la esqueletización sobre el
modelo hidráulico y la modelación de la calidad del agua de una RDAP. A continuación se
presentan los términos más relevantes para el desarrollo de este trabajo:
Potencia unitaria. Concepto que cuantifica la energía disipada por un tubo particular. Ésta resulta
del producto entre el caudal y la diferencia de altura piezométrica a lo largo del tubo (Saldarriaga,
Ochoa, Moreno, Romero, & Cortés, 2010):
[1]
Red Prototipo. Modelo hidráulico que presenta la información completa de la RDAP. Ésta
contiene los patrones de demanda originales e incluye todos los tubos que se encuentran
conectados. En este modelo no hay variación en los patrones de demanda y es útil para cuantificar
los resultados de la metodología propuesta.
Red Esqueletizada. Modelo con un menor número de nudos y tubos que la Red Prototipo que
representa adecuadamente las variables hidráulicas referentes a la presión en los nudos de consumo
de la RDAP.

Decaimiento de Cloro. En general, sustancias disueltas en una RDAP reaccionan con la masa de
agua así como con la pared de la tubería (Cortés et al, 2007); los dos tipos de reacciones deben ser
considerados en el momento de simular el decaimiento o crecimiento de una sustancia. En el caso
del cloro, éste reacciona tanto con la pared como con la masa de agua, lo cual hace que el contenido
total de cloro disminuya. El decaimiento de cloro es una función de primer orden la cual puede ser
descrita por medio de la siguiente expresión (Vasconcelos, Rossman, Grayman, & Boulos, 1997):
[2]
donde C es la concentración de cloro en el nudo de interés; Co es la concentración de cloro en el
nudo inmediatamente aguas arriba; K es el coeficiente de reacción; y T es el tiempo que se demora
una partícula de agua en el tubo que conecta al nudo de interés.
El coeficiente de reacción K es función del coeficiente de reacción de masa k
b
(bulk coefficient), el
coeficiente de reacción de pared k
w
(wall coefficient), y el coeficiente de transferencia de masa
desde el interior del fluido hacia las paredes k
f
(mass transfer coefficient). El k
f
depende de la
difusividad de las especies transportadas (en este caso, cloro), del diámetro del tubo y de las
características hidráulicas del flujo. Por lo anterior, el k
f
relativo a cierta sustancia puede ser
deducido automáticamente después de realizar el cálculo hidráulico de la red usando un programa
de simulación.
Por otra parte, k
b
y k
w
dependen de un número de variables (i.e. material de la tubería, edad de la
tubería, condiciones de la tubería e instalaciones de almacenamiento) y deben ser asignados por el
usuario a cada tubo de la RDAP (Walski, Chase, Savic, Grayman, Beckwith, & Koelle, 2003).
Las medidas de bondad de ajuste que serán utilizadas son las siguientes (Montgomery & Peck,
1982):
Coeficiente de determinación (R
2
). El coeficiente de determinación relaciona la varianza que es
considerada por efectos del modelo estadístico. Particularmente, el R
2
representa la proporción de
los datos que se encuentra más cerca a la línea de mejor ajuste, indicando la similitud entre las
variables de los modelos comparados. El valor del coeficiente de determinación varía entre 0 y 1,
siendo 1 el límite que representa una mejor determinación entre las muestras.
Coeficiente de correlación (R).
El R es una medida de comparación entre dos variables cuantitativas independiente de la escala de
medición. Su valor se encuentra en el rango real entre -1y 1.
Error cuadrático (EC). El EC representa el cuadrado de las diferencias entre el valor inferido de
una cantidad y su valor real.
Error cuadrático medio (ECM). El ECM es una función de riesgo, correspondiente al valor
esperado del error cuadrático. Éste mide el promedio de los cuadrados de los errores entre las
observaciones reales y las respuestas estimadas por un modelo.
Error medio absoluto (EMA). El EMA corresponde al valor esperado del error absoluto. Mide el
promedio de las diferencias absolutas entre los valores reales y los valores inferidos de cierta
cantidad.
Error absoluto máximo. Es la mayor de las diferencias absolutas entre los valores inferidos y los
valores reales de cierta cantidad.

METODOLOGÍA PARA MODELAR LA CALIDAD DEL AGUA DE UN MODELO
ESQUELETIZADO
La metodología propuesta consiste de dos etapas principales, la etapa de esqueletización y la de
preservación de la calidad del agua. La primera tiene cuatro pasos: agregación de demandas,
aplicación de una metodología tradicional de esqueletización, ramificación, y finalmente, tuberías
equivalentes (CIACUA, 2011).
1. Agregación de Demandas. A fin de reducir el número de nudos, la agregación de demandas
concentra las demandas independientes en un número menor de nudos de consumo
representativos. Este paso mantiene el balance de flujo en el sistema.
2. Algoritmo principal de esqueletización usando el criterio de Potencia Unitaria. Los
modelos esqueletizados de RDAP son generados por medio de la selección y eliminación de un
cierto número de nudos y tubos, manteniendo todos los nudos de consumo conectados al
sistema. Este proceso debe ser llevado a cabo de tal manera que el modelo reducido pueda
representar el comportamiento hidráulico del prototipo de manera adecuada (la presión se
mantiene, pero el caudal cambia debido a la reducción en el número de tubos). Este paso
involucra un procedimiento iterativo en el que, en cada iteración, el tubo con la menor PU es
removido de la red y el modelo generado mantiene todos los nudos de consumo conectados. Se
prueban todos los tubos, y el que genere el mínimo impacto en el desempeño hidráulico de la
red se elimina permanentemente del modelo. Este procedimiento es realizado tantas veces
como sean definidas por el diseñador.
3. Ramificación. Este paso busca la eliminación de nudos cuyo consumo sea despreciable y que
no tengan consumos aguas abajo. Con estos se eliminan también las tuberías que los conectan,
es decir, se eliminan los extremos libres que no tienen caudales representativos.
4. Tuberías equivalentes. Éste es un procedimiento que remplaza tuberías en serie, cuyos nudos
no tienen demanda, por una tubería simple que genera pérdidas de energía (por fricción y
menores) equivalentes.
Después de aplicar este procedimiento, el modelo hidráulico simplificado resultante es bastante
preciso en términos de la presión en los nudos, respetando todos los caudales demandados. En el
caso del caudal en cada tubo, el modelo simplificado tiende a cambiar los valores originales a fin de
cumplir con la conservación de la masa. Esto causa que tanto la calidad de agua como los tiempos
de retención en el modelo esqueletizado no coincidan con las condiciones de la red prototipo. El
siguiente paso de la metodología propuesta, busca resolver este inconveniente aplicando una serie
de correcciones al modelo esqueletizado, con el propósito de ajustar el modelo de calidad del agua
para que éste represente adecuadamente la red prototipo.
5. Corrección calidad de agua por escalas adimensionales. La forma en que la concentración
de cloro varía entre el modelo prototipo y el esqueletizado es diferente para cada nudo de la
red. Esto implica que el factor de corrección debe variar de un nudo a otro, para así obtener una
buena aproximación de la calidad del agua en todo el sistema. Para este propósito, en esta
nueva metodología se utilizan parámetros adimensionales (PA) a fin de modificar de manera
individual la concentración de cloro de cada nudo en el modelo esqueletizado. La idea es seguir
los criterios de similitud dinámica de la Mecánica de Fluidos, en términos de números
adimensionales.
Los PA se obtienen calculando el cociente entre el valor de una propiedad hidráulica en el modelo
esqueletizado y su valor en el prototipo. Las propiedades que son tenidas en cuenta, en esta
metodología, son caudal en los tubos y edad del agua en los nudos. Los PA de caudal y edad del
agua se calculan como se muestra a continuación, respectivamente:

[3]
[4]
Para la aplicación de estos PA se consideraron dos aproximaciones diferentes. La primera consiste
en aplicar la corrección al cálculo de la concentración de cloro, multiplicando el caudal en cada
tubo del modelo esqueletizado por su PA correspondiente, y posteriormente corriendo la simulación
de calidad del agua (con los caudales modificados) para así obtener la concentración de cloro
ajustada. En este caso, el caudal en cada tubo es corregido, bien sea por su correspondiente PA de
caudal o por el PA de edad del agua del nudo inmediatamente aguas abajo. Si se tiene en cuenta las
ecuaciones de decaimiento del cloro en una RDAP, es claro que estos PA son los que mejor
describen el fenómeno de correlación prototipo-modelo esqueletizado.
La segunda aproximación consiste en aplicar la corrección directamente a la concentración de cloro,
multiplicando el valor de dicha concentración en cada uno de los nudos del modelo esqueletizado
por su correspondiente parámetro adimensional de edad del agua. El producto de esta multiplicación
es la concentración de cloro ajustada.
A pesar de que ambas aproximaciones presentan mejores ajustes sobre la calidad de agua de los
modelos esqueletizados, la aproximación presentada en este trabajo es la segunda; es decir, aquella
que aplica los parámetros adimensionales directamente sobre el valor de la concentración de cloro.
Esto se realizó de esta forma debido a que presenta un ajuste mayor entre los valores de
concentración de cloro en el modelo prototipo y en el modelo esqueletizado. En cuanto a la segunda
aproximación, los parámetros adimensionales son elevados a diferentes potencias que varían en el
rango [0,1], para así obtener múltiples ajustes de la concentración de cloro de cada nudo en el
modelo esqueletizado.
Según esto, la corrección para cada nudo en el modelo esqueletizado se calcula de la siguiente
manera:
[5]
donde
es la concentración de cloro ajustada, PA es el parámetro adimensional
(
para este estudio), X es el exponente y
es la concentración
de cloro en el modelo esqueletizado, sin ningún tipo de corrección.
Cada exponente evaluado resulta en una concentración propia para cada nudo de la RDAP en el
modelo esqueletizado. Posteriormente, se realiza un análisis de sensibilidad a fin de identificar el
exponente que permita el mejor ajuste respecto a las concentraciones de cloro del prototipo. Este
análisis consiste en comparar la serie de concentraciones obtenida para un exponente, con los
valores de las concentraciones de cloro de los nudos comparables del modelo prototipo. Para cada
serie de datos, se calcularon las medidas de bondad de ajuste con respecto a las concentraciones
originales. Finalmente, las medidas usadas se grafican para cada una de las correcciones
consideradas, obteniendo así el exponente que muestra mayor correlación entre los valores del
modelo prototipo y el esqueletizado. Las medidas mencionadas son: coeficiente de determinación
(R
2
), coeficiente de correlación (R), error cuadrático (EC), error cuadrático medio (ECM), error
medio absoluto (EMA) y error absoluto máximo.
CASOS DE ESTUDIO
El presente documento incluye el análisis de dos casos de estudio. Éstos se basan en RDAPs reales,
pero con diferentes propiedades hidráulicas y características topológicas. La primera RDAP
pertenece al municipio colombiano de Andalucía Alta y la segunda al municipio colombiano de
Guacarí, ambos ubicados en el Departamento del Valle del Cauca, Colombia.
Para ambas redes se aplicó la metodología propuesta y se obtuvieron resultados satisfactorios. A
continuación se presentan los dos casos de estudio.
Andalucía Alta (CIACUA, 2005)
Andalucía es un municipio del Departamento del Valle del Cauca, Colombia. Esta RDAP ha sido
estudiada previamente por el CIACUA (2011). Está integrada por 360 tubos, 329 nudos, y 992
msnm de altura piezométrica a la entrada. Tiene una longitud total de tuberías de 26400 m y una
demanda total de 20 L/s. Los tubos son de PVC con una rugosidad absoluta de 0.0015 mm y
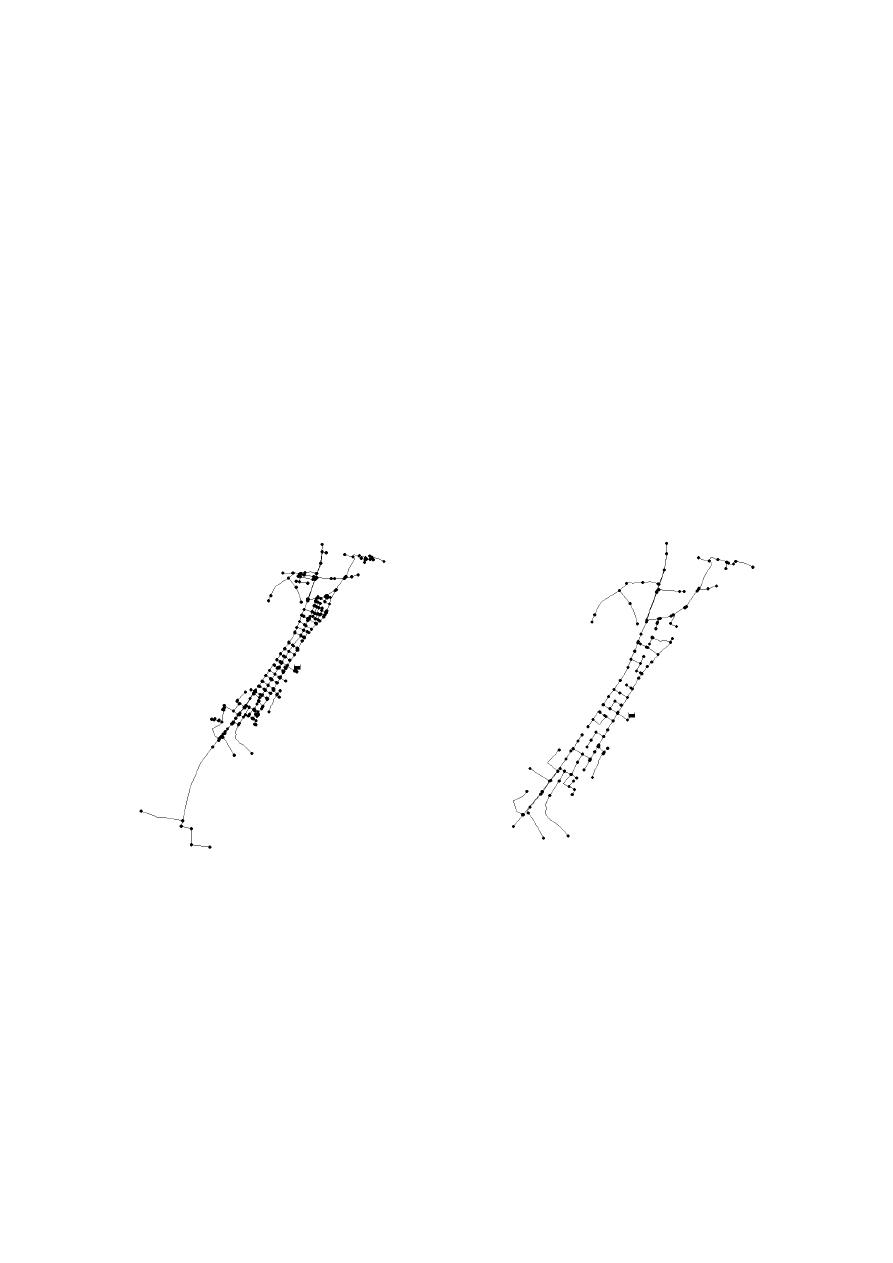
diámetros comerciales disponibles entre 50 mm (2”) y 100 mm (4”). En la Figura 1 se ilustra la
topología de esta red. Adicionalmente se presenta el modelo una vez ha sido aplicada la
metodología de esqueletización.
(a)
(b)
Figura 1. a) -Modelo prototipo, Andalucía. b) –Modelo esqueletizado, Andalucía.
Guacarí (CIACUA, 2005)
La segunda RDAP es Guacarí, la cual se encuentra ubicada también en el Departamento del Valle
del Cauca, Colombia. Está integrada por 656 tubos, 571 nudos, y 1100 msnm de altura piezométrica
a la entrada. Tiene una longitud total de tuberías de 56840 m y una demanda total de 47 L/s. Los
tubos están hechos de PVC con una rugosidad absoluta de 0.0015 mm y disponibles en diámetros
comerciales entre 50 mm (2”) y 100 mm (4”). La Figura 2 ilustra la topología de esta red, así como
el modelo una vez ha sido esqueletizado.
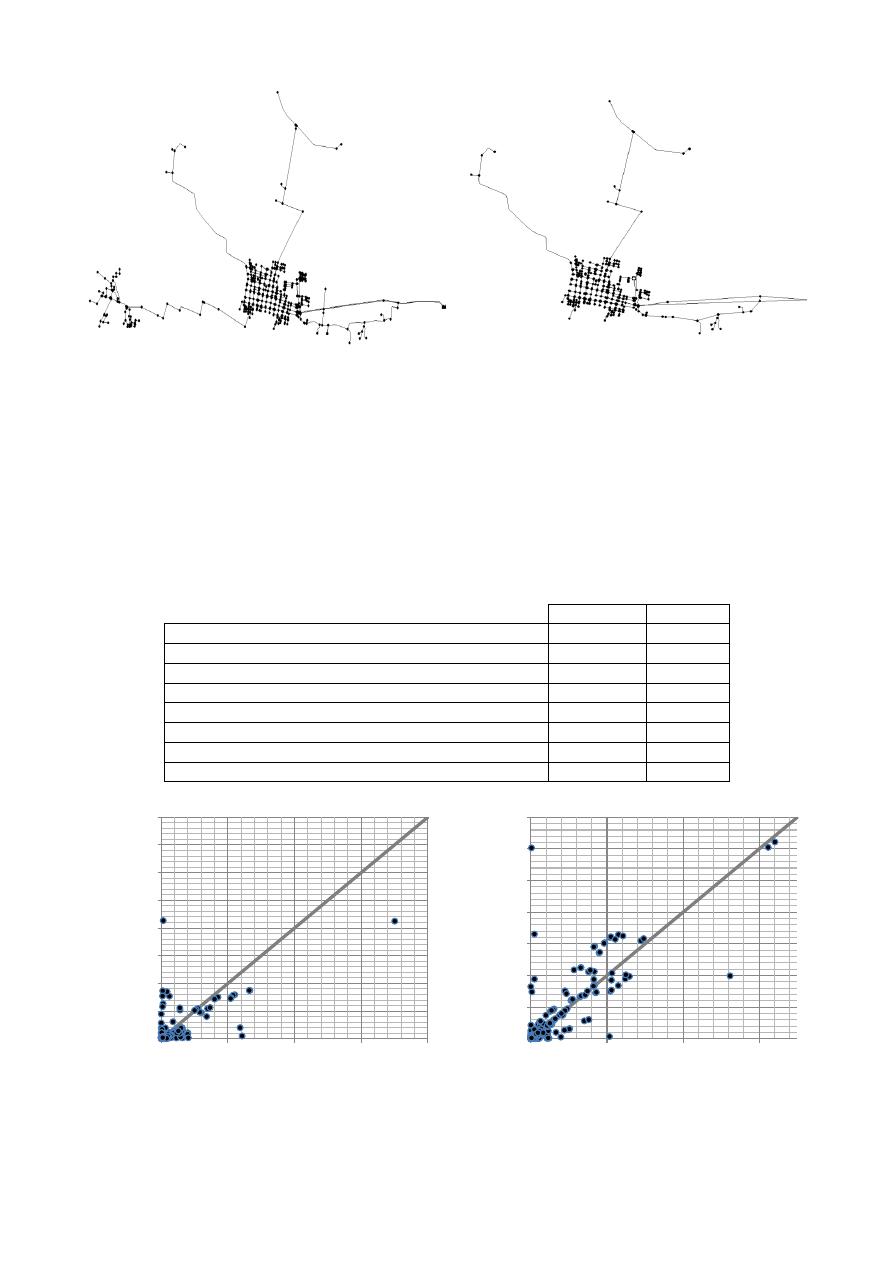
(a)
(b)
Figura 2. a) - Modelo prototipo, Guacarí. b) - Modelo esqueletizado, Guacarí.
RESULTADOS
Los resultados obtenidos una vez aplicada la metodología tradicional de esqueletización y las
correcciones en la concentración del cloro propuestas se presentan a continuación. La Tabla 1
muestra el efecto de la metodología tradicional de esqueletización para cada caso de estudio, así
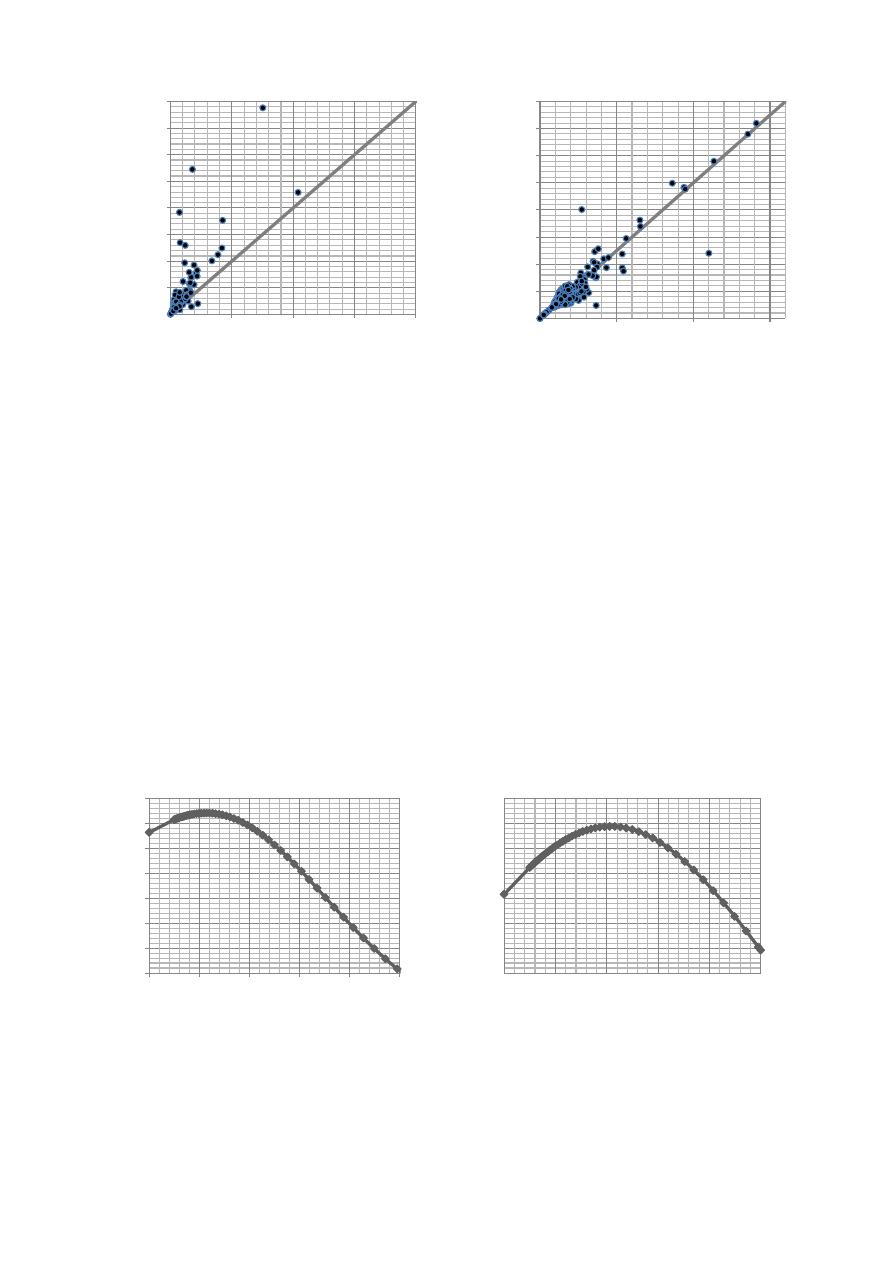
como la Figura 3 y la Figura 4 muestran los cambios de Caudal y Tiempo de Residencia (TR), una
vez aplicada dicha metodología. En estas figuras las diferencias de caudal y TR son altas, lo cual
impide una buena modelación de la calidad de agua en los nudos.
Tabla 1. -Efectos de la metodología tradicional de esqueletización sobre las redes de Andalucía y
Guacarí.
Andalucía
Guacarí
Nudos en el Modelo Prototipo
329
571
Nudos en el Modelo Esqueletizado
144
413
Disminución de nudos
56%
28%
Tubos en el Modelo Prototipo
360
656
Tubos en el Modelo Esqueletizado
145
414
Disminución de tubos
60%
37%
Error relativo promedio de las presiones
5%
0.5%
Error relativo promedio de las concentraciones de cloro
115%
1020%
(a)
(b)
Figura 3.
Comparación del caudal en cada tubo en el prototipo y en el modelo esqueletizado
por medio de la metodología tradicional de esqueletización.
a) -
Andalucía. b
) -
Guacarí.
0
0.005
0.01
0.015
0.02
0.025
0.03
0.035
0.04
0.00
0.01
0.02
0.03
0.04
C
audal
, M
ode
lo
Es
que
le
ti
zado
(m
3
/s)
Caudal, Modelo Original (m
3
/s)
0
0.005
0.01
0.015
0.02
0.025
0.03
0.035
0.00
0.01
0.02
0.03
C
audal
, M
ode
lo
Es
que
le
ti
zado
(m
3
/s)
Caudal, Modelo Original (m
3
/s)
(a)
(b)
Figura 4.
Comparación de tiempo de residencia en cada nodo en el prototipo y en el modelo
esqueletizado por la metodología tradicional de esqueletización.
a) -
Andalucía. b
) -
Guacarí.
De acuerdo con los datos mostrados en la Tabla 1, la metodología tradicional de esqueletización
permitió una reducción sustancial en el tamaño de ambas RDAP. Adicionalmente, los errores
relativos promedio obtenidos para las presiones son mínimos, lo cual garantiza una modelación
precisa de la hidráulica de las dos redes. Esto se ve reflejado en la tendencia que presentan la
mayoría de los puntos en la Figura 3 a estar cerca a la línea de 45º, a pesar de que existen tubos en
los que el cambio de caudal es alto. Sin embargo, los errores relativos promedio de las
concentraciones de cloro son particularmente altos, y debido a esto, las concentraciones resultantes
deben ser corregidas para lograr conseguir una modelación confiable de la calidad del agua. Lo
anterior se debe en parte a los cambios que hay en el Tiempo de Resiliencia entre los modelos
originales y los esqueletizados (Figura 4).
Por medio de la aplicación de la metodología propuesta en este trabajo se obtiene una gráfica de
sensibilidad para cada caso de estudio. El análisis de sensibilidad presenta el valor del coeficiente
de determinación R
2
como función del exponente del PA seleccionado. Los modelos esqueletizados
junto con las gráficas mencionadas se presentan en la Figura 5.
(a)
(b)
Figura 5. a) - Gráfica de sensibilidad para Andalucía. b) - Gráfica de sensibilidad para Guacarí.
El análisis de sensibilidad indica que, siguiendo la metodología propuesta, el R
2
puede ser ajustado
hasta un valor máximo de 0.94 para ambos casos de estudio. Así, los exponentes más adecuados son
0.23 y 0.41, para la red de Andalucía y la de Guacarí respectivamente.
0
50000
100000
150000
200000
250000
300000
350000
400000
0
100000
200000
300000
400000
TR,
M
ode
lo
Es
que
le
ti
zado
(s
e
g)
TR, Modelo Oringinal (seg
)
0
20000
40000
60000
80000
100000
120000
140000
160000
0
50000
100000
150000
TR,
M
ode
lo
Es
que
le
ti
zado
(s
e
g)
TR, Modelo Oringinal (seg)
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0
0.2
0.4
0.6
0.8
1
C
oe
fi
ci
e
nt
e
de
D
e
te
rm
inaci
ón
(R
2
)
Exponente
0.65
0.70
0.75
0.80
0.85
0.90
0.95
1.00
0
0.2
0.4
0.6
0.8
1
C
oe
fi
ci
e
nt
e
de
D
e
te
rm
inaci
ón
(R
2
)
Exponente
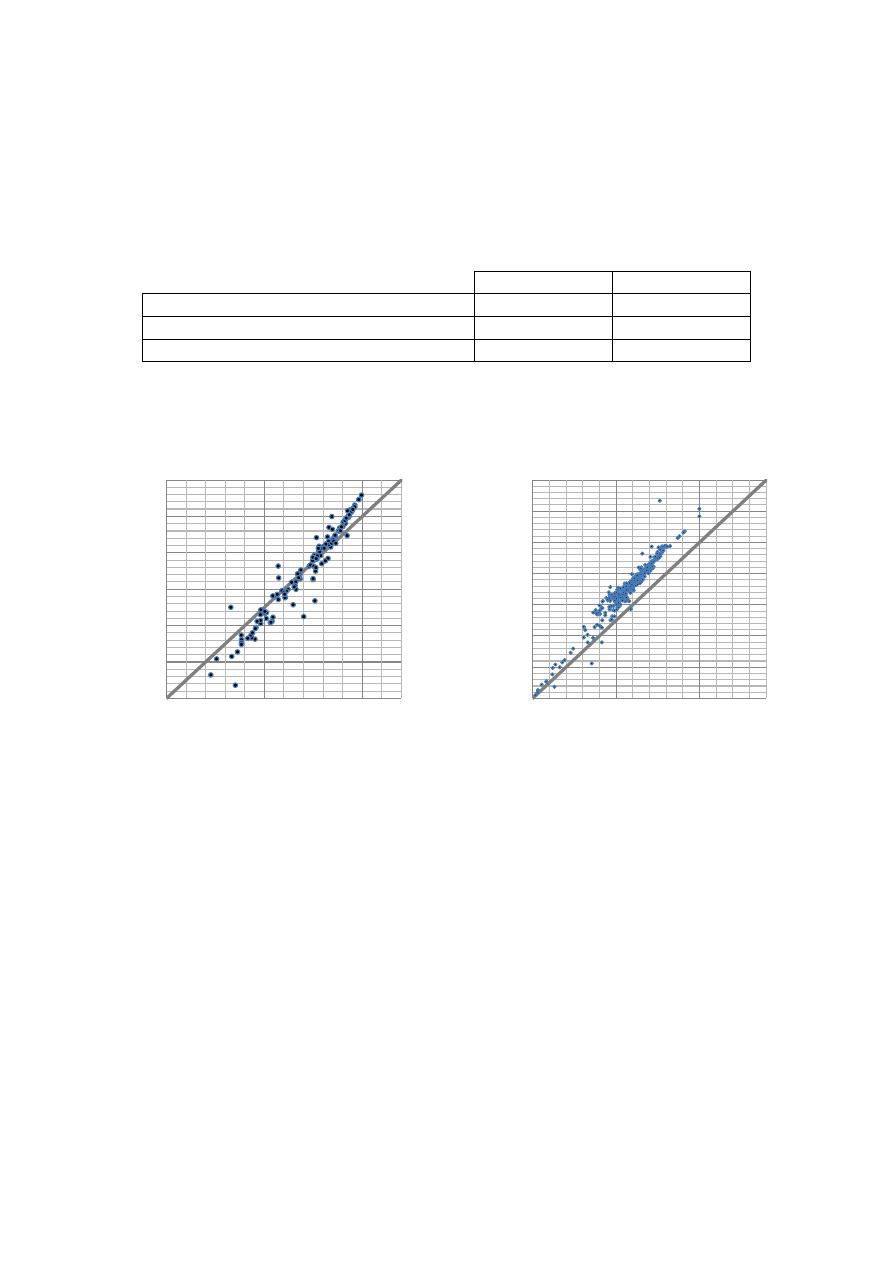
Una comparación entre la metodología tradicional y la propuesta se presenta en la Tabla 2, con
respecto al coeficiente de determinación obtenido por medio de cada proceso. Para ambos casos de
estudio los resultados, luego de aplicar la metodología propuesta, mejoran la modelación de la
calidad de agua en los modelos esqueletizados. Los coeficientes de correlación para la
concentración de cloro residual en los nodos aumentan ostensiblemente.
Tabla 2. -R
2
obtenido por medio de la metodología tradicional de esqueletización y la metodología
propuesta.
Andalucía
Guacarí
R
2
Metodología tradicional
0.86
0.81
R
2
Metodología propuesta
0.94
0.94
Variación
9%
16%
Finalmente, los resultados son graficados para cada caso de estudio con el propósito de comparar la
concentración de cloro en el modelo prototipo con la concentración de cloro en el modelo obtenido
por medio de la metodología propuesta (Figura 6).
(a)
(b)
Figura 6. a) -Comparación entre la concentración de cloro en el prototipo y en el modelo
esqueletizado por medio de la metodología propuesta, Andalucía. b) -Comparación entre la
concentración de cloro en el prototipo y en el modelo esqueletizado, Guacarí.
Como se pude ver en la Figura 6, para ambas RDAP bajo estudio, los modelos esqueletizados con
capaces de reproducir bastante bien la concentración de cloro en los nudos. Las diferencias más
notables se encuentran en aquellos nudos más alejados de las fuentes o que se encuentren en zonas
relativamente aisladas de las redes. Los coeficientes de correlación resultaron ser bastante altos en
los dos casos. Adicionalmente, se puede afirmar que los resultados de las concentraciones de cloro
residual encontradas en modelos esqueletizados permiten simular modelos operativos en corto
tiempo a fin de garantizar la correcta prestación del servicio de suministro de agua potable.
CONCLUSIONES
Las metodologías tradicionales de esqueletización no representan adecuadamente la concentración
de cloro. La razón es el cambio de la velocidad de flujo y el caudal del modelo esqueletizado con
respecto al prototipo. Debido a esta variación, es necesario usar diferentes parámetros
adimensionales que modifiquen individualmente la concentración de cloro en cada punto de la
RDAP.
0
0.2
0.4
0.6
0.8
1
1.2
0
0.5
1
C
once
nt
raci
ón
de
C
loro,
M
e
todol
ogí
a
P
ropue
st
a
(m
g/L)
Concentración de Cloro, Modelo Original (mg/L)
0
0.2
0.4
0.6
0.8
1
1.2
1.4
0
0.5
1
C
once
nt
raci
ón
de
C
loro,
M
e
todol
ogí
a
P
ropue
st
a
(m
g/L)
Concentracion de Cloro, Modelo Original (mg/L)

La aplicación de la metodología de esqueletización de calidad del agua produce modelos reducidos
que son significativamente más pequeños que los prototipos y que pueden reproducir
satisfactoriamente tanto el modelo hidráulico como el de concentración de cloro de la red prototipo.
Por tanto, esta metodología constituye una herramienta bastante útil para operadores y diseñadores
de RDAP.
Las medidas de bondad de ajuste cuantifican las diferencias entre las concentraciones de cloro de la
red prototipo y las del modelo esqueletizado. Por medio de un análisis de sensibilidad, es posible
encontrar los parámetros adimensionales más apropiados para ajustar la calidad en el modelo
esqueletizado. Para ambos casos de estudio, el coeficiente de determinación R
2
, obtenido mediante
la comparación del modelo prototipo y el modelo esqueletizado (incluyendo la corrección por
calidad de agua propuesta en este artículo) fue mayor a 0.94.
REFERENCIAS
CIACUA, (2006). Programa REDES. Universidad de los Andes. Bogotá D.C., Colombia.
Cortés, O., Saldarriaga, J. (2007) Modelación de la calidad del agua en sistemas de distribución
de agua potable en período extendido. Tesis de Magíster, Universidad de los Andes,
Departamento de Ingeniería Civil y Ambiental, Bogotá, Colombia.
Duzinliewicz, K., & Ciminski, A. (2006). Drinking Water Distribution System Modelling - An
approach to skeletonization. Applications of Large Scale Industrial Systems, Volume # 1 | Part#
1. Finland.
Grayman, W. M., & Rhee, H. (2004). Assessment of Skeletonization in Network Models.
Proceedings of the 2000 Joint Conference on Water Resources Engineering and Water Resources
Planning & Management, Minneapolis, Minnesota
Janke, R., Murray, R., Uber, J., Bahadur, R., Taxon, T., Samuels, W., y otros. (2007). Using
TEVA to Asses Impact of Model Skeletonization on Contaminant Consequence Assessment and
Sensor Placement Design. Proceedings of the 2007 World Environmental and Water Resources
Congress, Tampa, Florida.
Montgomery, D. C., & Peck, E. A. (1982). Introduction to linear regression analysis. Atlanta, GA
USA: John Wiley & Sons.
Perelman, L., Masli, M. L., Ostfeld, A., & Sautner, J. B. (2008). Ussing
aggregation/skeletonization network models for water quality simulations in epidemiologic
studies. Journal AWWA , 122-133.
John J Vasconcelos; Lewis A Rossman; Walter M Grayman y Paul F Boulos (1997). Kinetics
of Chlorine Decay. American Water Works Association. Journal; Jul 1997; 89, 7; ABI/INFORM
Trade & Industry pg. 54.
J. Powell, J. West, N. Hallam y C. Forster (2000). Performance of various kinetic models for
chlorine decay. Journal of Water Resources Planning and Management, Vol. 126, No. 1, pp. 13-
20.
R. Janke, R. Murray, J. Uber y R. Bahadur (2009). Using TEVA to Assess Impact of Model
Skeletonization
on
Contaminant
Consequence
Assessment
and
Sensor
Placement
Design.Diciembre.
Saldarriaga, J. (2007). Hidráulica de Tuberías. Universidad de los Andes, Bogotá Colombia.
Alfaomega, ISBN: 9789586826808.
Saldarriaga, J; Ochoa S. Nieto, L & Rodriguez, D. (2009). Methodology for the Skeletonization
of Water Distribution Network Models with Demand Aggregation. Computing and Control in
the Water Industry Integrating Water Systems. The Edge, University of Sheffield.
Saldarriaga, J.C., Ochoa, S., Rodríguez D., & Arbeláez J. Water Distribution Network
Skeletonization Using Resilience Concept”. Network Resilience and Resilience Index.
Todini, E., (2000). Looped water distribution networks design using a resilience index based
heuristic approach. Urban Water, 2(3), 115 – 122.
Todini, E., (2008). Design, expansion and rehabilitation of water distribution networks aimed at
reducing water losses. Where are we? Proceedings of the 10th International Water Distribution
System Analysis Conference 2008, Kruger National Park, South Africa.
Ulanicki, B., Zehnpfund, A., & Martinez, F. (1996). Simplification of Water Distribution
Network Models. Proceedings of the Hydroinformatics 96 International Conference,
International Association for Hydraulic Research, Zürich.
Walski, T. M., Chase, D. V., Savic, D. A., Grayman, W., Beckwith, S., & Koelle, E. (2003).
Advanced water distribution modeling and management. Waterbury, CT USA: Haestad Press.
