
TESIS DE PREGRADO
ALGORITMO DE REDONDEO DE DIÁMETROS DENTRO DEL MÓDULO DE
DISEÑO DEL PROGRAMA REDES
Juan Felipe García Acero
Asesor: Juan G. Saldarriaga Valderrama
UNIVERSIDAD DE LOS ANDES
FACULTAD DE INGENIERÍA
DEPARTAMENTO DE INGENIERÍA CIVIL Y AMBIENTAL
PREGRADO EN INGENIERÍA CIVIL
BOGOTÁ D.C.
2013

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
i
Bogotá, Diciembre de 2013
Agradecimientos
Un especial agradecimiento al Ingeniero Juan Guillermo Saldarriaga Valderrama, asesor de esta
tesis, por la gran ayuda, guía y asistencia proporcionada sin la cual este proyecto no hubiera sido
posible desarrollar. A su vez un agradecimiento especial a Diego Alejandro Páez y Laura Lunita
Lopez por su apoyo y aportes en la realización de este proyecto de grado. Así mismo un
agradecimiento a todo el personal del Centro de investigaciones de Acueducto y Alcantarillado
(CIACUA) por los consejos y apoyo. Gracias a Dios, a mis amados Padres, Mauricio García Triana y
Mary Acero Baracaldo y a todos los que han creído en mí y siempre me han brindado su apoyo y
estímulo.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
ii
Resumen
Dado que los recursos para construir Redes de Distribución de Agua Potable (RDAP) son limitados,
se hace indispensable contar con diseños óptimos, tanto desde el punto de vista económico como
hidráulico, para así obtener el máximo beneficio.
Identificar el diseño más eficiente y menos costoso para una red de distribución de agua potable
(RDAP) es un problema complejo. Históricamente se ha hecho uso de métodos de búsqueda
adaptativa (ASM por sus siglas en inglés). Estos métodos se basan en algoritmos computacionales
extraídos de los procesos naturales, y que han surgido como una alternativa eficaz para la solución
de problemas de este tipo pues utilizan variables discretas a diferencia de los métodos de
optimización lineal. Sin embargo es posible plantear una metodología para la mejora de un diseño
óptimo local obtenido como resultado del redondeo de una solución óptima global en términos
continuos.
Este trabajo plantea dicho procedimiento, que combina una metodología hidráulica conocida
como OPUS y un algoritmo heurístico conocido como Algoritmo Voraz que se utilizaron para
alcanzar la mejor combinación de ajustes del diseño modificado que estaría en más estrecha
alineación con el óptimo global. Con el fin de probar el desempeño de la metodología se hicieron
simulaciones con las redes Balerma, Hanoi, Taichung y R28. Con los resultados obtenidos se
demuestra la ventaja del uso de OPUS como inicio en caliente, el desempeño de la metodología
propuesta y las ventajas y limitaciones de los calculadores hidráulicos utilizados en el programa
REDES.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
iii
Tabla de Contenido
ÍNDICE DE FIGURAS ................................................................................................................................................................................vi
ÍNDICE DE TABLAS ............................................................................................................................................................................... vii
1.
INTRODUCCIÓN Y OBJETIVOS ................................................................................................................................................... 1
1.1.
Introducción. ....................................................................................................................... 1
1.2.
Objetivo General. ................................................................................................................ 3
1.3.
Objetivos Específicos. .......................................................................................................... 3
2.
MARCO TEÓRICO ........................................................................................................................................................................... 4
2.1.
Descripción del problema de diseño de redes de distribución de agua potable ................ 4
2.1.1.
Definición del problema .............................................................................................. 4
2.1.2.
Restricciones del problema ......................................................................................... 5
Restricciones hidráulicas ............................................................................................................. 5
Restricciones comerciales ........................................................................................................... 8
Otras restricciones ...................................................................................................................... 8
2.2.
Incógnitas y ecuaciones del problema .............................................................................. 12
2.3.
Complejidad del problema ................................................................................................ 13
2.4.
Aproximaciones al problema del diseño de redes de distribución de agua potable ........ 14
2.4.1.
Aproximación tradicional al problema del diseño de RDAP ..................................... 14
2.5.
Metodologías de diseño optimizado de RDAP desarrolladas recientemente a nivel
mundial ......................................................................................................................................... 15
2.5.1.
Algoritmos genéticos ................................................................................................. 15
2.5.2.
Búsqueda de Armonía (Harmony Search) ................................................................. 16
2.5.3.
Recocido Simulado (Simulated Annealing) ............................................................... 17
2.5.4.
Búsqueda Tabú (tabu search) .................................................................................... 18
2.5.5.
Criterio geométrico de diseño propuesto por I Pai Wu ............................................ 19
Aplicación del criterio de I Pai Wu al caso de RDAP .................................................................. 20
Criterio de featherstone (1983) ................................................................................................ 20
2.5.6.
Superficie óptima de presiones (SOP, villalba, 2004) ................................................ 21
Cálculo de las distancias a las fuentes ....................................................................................... 22
Ecuaciones para modelar la caída de la altura piezométrica ideal de nudo a nudo ................. 22

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
iv
2.5.7.
Metodología de superficie óptima de gradiente hidráulico (SOGH) ......................... 23
2.5.6.
Metodología de Optimal Power Use Surface (OPUS) ............................................... 25
2.6.
Programas ......................................................................................................................... 30
2.6.6.
Programa REDES ........................................................................................................ 30
2.6.7.
Programa EPANET ..................................................................................................... 31
2.7.
Metodología de redondeo, aumento y disminución de diámetros (RAD) desarrollada
para OPUS en el programa REDES ................................................................................................. 32
2.7.6.
Metodología de redondeo de diámetros y posterior optimización .......................... 32
Etapa de redondeo de diámetros ............................................................................................. 33
2.7.7.
Redondeo aproximando al siguiente/anterior diámetro comercial ......................... 33
2.7.8.
Redondeo aproximando a la Potencia ...................................................................... 34
Etapa de optimización ............................................................................................................... 36
2.7.9.
Algoritmo de aumentar diámetros ........................................................................... 37
2.7.10. Algoritmo de disminuir diámetros ............................................................................ 40
2.7.11. Uso de la metodología de redondeo, aumento y disminución de diámetros
desarrollada para OPUS en el programa redes. ........................................................................ 42
3.
METODOLOGÍA PROPUESTA PARA LA APROXIMACIÓN DE DIÁMETROS EN LA FASE FINAL DEL DISEÑO
OPTIMIZADO DE REDES DE DISTRIBUCIÓN DE AGUA .................................................................................................................. 48
3.1.
Metodología de inicio en caliente ..................................................................................... 48
3.2.
Heurística de Postoptimization: Algoritmo Voraz ............................................................. 48
3.2.1.
Definición .................................................................................................................. 49
3.2.2.
Hot Start: Redondeo solución OPUS ......................................................................... 49
3.2.3.
Algoritmo Voraz o Greedy Algorithm ........................................................................ 51
3.2.4.
Regla de decisión ponderada .................................................................................... 55
4.
EVALUACIÓN DEL DESEMPEÑO DE LA METODOLOGÍA PROPUESTA ............................................................................ 59
4.1.
Uso de la metodología propuesta desarrollada para OPUS en el programa REDES ......... 59
4.2.
Red Hanoi .......................................................................................................................... 64
4.3.
Red Balerma ...................................................................................................................... 65
4.4.
Red Taichung ..................................................................................................................... 67
4.5.
Red R28 ............................................................................................................................. 68
4.6.
Relación de los resultados ................................................................................................. 70

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
v
5.
CONCLUSIONES ........................................................................................................................................................................... 75
6.
RECOMENDACIONES .................................................................................................................................................................. 77
7.
REFERENCIAS ............................................................................................................................................................................... 78
ANEXOS .................................................................................................................................................................................................... 81

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
vi
ÍNDICE DE FIGURAS
F
IGURA
1
C
RITERIO DE
I-
PAI
W
U
.
(O
CHOA
,
2009) ...................................................................................................... 19
F
IGURA
2
C
RITERIO DE
I-
PAI
W
U
.
O
CHOA
(2009) ...................................................................................................... 21
F
IGURA
3
D
IAGRAMA
BPMN
DE LA METODOLOGÍA
OPUS.
S
ALDARRIAGA
(2013). ........................................................... 26
F
IGURA
4
R
ELACIÓN ESQUEMÁTICA ENTRE EL COSTO DE TUBERÍA Y CAUDAL
.
S
ALDARRIAGA
(2013). ...................................... 27
F
IGURA
5
E
L CRITERIO DE LA
I-
P
AI
W
U PARA PREDEFINIR LA ALTURA EN CADA NUDO
.
S
ALDARRIAGA
(2013). ........................ 27
F
IGURA
6
V
ENTANA DEL PROGRAMA
REDES
2013
CON LA
R
ED
B
ALERMA
. ...................................................................... 42
F
IGURA
7
V
ENTANA PARA INGRESAR LAS OPCIONES DE DISEÑO DEL MODULO
OPUS. .......................................................... 43
F
IGURA
8
V
ENTANA PARA ELEGIR EL TIPO DE REDONDEO DESEADO
. ................................................................................. 44
F
IGURA
9
V
ENTANA DE OPCIONES DE DISEÑO CON LISTA DE CRITERIOS PARA AUMENTAR DIÁMETROS
. .................................... 45
F
IGURA
10
V
ENTANA DE PARA INGRESAR LOS PARÁMETROS GENERALES DE LA RED
. ............................................................ 46
F
IGURA
11
V
ENTANA DE PARA INGRESAR ALGUNOS PARÁMETROS DEL DISEÑO
................................................................... 47
F
IGURA
12
V
ENTANA DE PARA INGRESAR ALGUNOS PARÁMETROS DEL DISEÑO
................................................................... 47
F
IGURA
13
V
ENTANA DE PARA INGRESAR EL MÉTODO DE APROXIMACIÓN
. ........................................................................ 59
F
IGURA
14
V
ENTANA DE PARA INGRESAR ELEGIR ENTRE EL REDONDEO SIMPLE AL SIGUIENTE O EL
A
LGORITMO
V
ORAZ
.............. 60
F
IGURA
15
V
ENTANA DE PARA INGRESAR LOS PARÁMETROS DEL
A
LGORITMO
V
ORAZ
“G
REEDY
A
LGORITHM
”.......................... 61
F
IGURA
16
RDAP
H
ANOI
.
L
AS ETIQUETAS MUESTRAN LOS NÚMEROS DE IDENTIFICACIÓN DE LAS TUBERÍAS Y NUDOS
. ............... 64
F
IGURA
17
RDAP
B
ALERMA
. .................................................................................................................................. 66
F
IGURA
18
RDAP
T
AICHUNG
.................................................................................................................................. 67
F
IGURA
19
RDAP
R28.
L
AS ETIQUETAS MUESTRAN LOS NÚMEROS DE IDENTIFICACIÓN DE TUBERÍAS Y NODAL
. ........................ 69

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
vii
ÍNDICE DE TABLAS
T
ABLA
1.
E
SCENARIO DOS FACTORES
:
S
UBCONJUNTOS DE FACTORES Y PESOS DE LOS FACTORES
. ........................................... 62
T
ABLA
2.
E
SCENARIO TRES FACTORES
:
S
UBCONJUNTOS DE FACTORES Y PESOS DE LOS FACTORES
. ........................................... 62
T
ABLA
3.
E
SCENARIO CUATRO FACTORES
:
S
UBCONJUNTOS DE FACTORES Y PESOS DE LOS FACTORES
. ...................................... 63
T
ABLA
4.
R
ESULTADOS OBTENIDOS PARA LA RED
H
ANOI
. ............................................................................................... 65
T
ABLA
5.
R
ESULTADOS OBTENIDOS PARA LA RED
B
ALERMA
. ........................................................................................... 66
T
ABLA
6.
R
ESULTADOS OBTENIDOS PARA LA RED
T
AICUNG
............................................................................................. 68
T
ABLA
7.
R
ESULTADOS OBTENIDOS PARA LA RED
R28. .................................................................................................. 69
T
ABLA
8.
R
ESULTADOS OBTENIDOS PARA LA METODOLOGÍA
RAD-OPUS
CON EL CALCULADOR HIDRÁULICO
S
PARSE
S
OLVER
...... 70
T
ABLA
9.
R
ESULTADOS OBTENIDOS PARA LA METODOLOGÍA
RAD-OPUS
CON EL CALCULADOR HIDRÁULICO
S
PARSE
S
OLVER
. ..... 71
T
ABLA
10.
R
ESULTADOS OBTENIDOS PARA LA METODOLOGÍA
RAD-OPUS
CON EL CALCULADOR HIDRÁULICO
E
PANET
. ............. 71
T
ABLA
11.
R
ESULTADOS OBTENIDOS PARA LA METODOLOGÍA
G
REEDY
A
LGORITHM CON EL CALCULADOR HIDRÁULICO
S
PARSE
S
OLVER
. ............................................................................................................................................ 72
T
ABLA
12.
R
ESULTADOS OBTENIDOS PARA LA METODOLOGÍA
G
REEDY
A
LGORITHM CON EL CALCULADOR HIDRÁULICO
E
PANET
. .. 72
T
ABLA
13.
P
ESO DE LOS PONDERADORES PARA LOS MEJORES RESULTADOS OBTENIDOS PARA LA METODOLOGÍA
G
REEDY
A
LGORITHM CON EL CALCULADOR HIDRÁULICO
S
PARSE
S
OLVER
. ............................................................................. 73
T
ABLA
14.
P
ESO DE LOS PONDERADORES PARA LOS MEJORES RESULTADOS OBTENIDOS PARA LA METODOLOGÍA
G
REEDY
A
LGORITHM CON EL CALCULADOR HIDRÁULICO
E
PANET
. ....................................................................................... 73
T
ABLA
15.
R
ANGO DE VALORES PARA LOS PARÁMETROS PONDERADORES DE LA REGLA DE DECISIÓN
....................................... 74
T
ABLA
16.
V
ALORES INGRESADOS COMO PARÁMETROS AL PROGRAMA
REDES
2013. ........................................................ 81
T
ABLA
17.
P
RUEBA DEL ESCENARIO DE DOS FACTORES PARA EL CALCULADOR
S
PARSE
S
OLVER
. .............................................. 82
T
ABLA
18.
P
RUEBA DEL ESCENARIO DE DOS FACTORES PARA EL CALCULADOR
E
PANET
. ........................................................ 84
T
ABLA
19.
P
RUEBA DEL ESCENARIO DE TRES FACTORES PARA EL CALCULADOR
S
PARSE
S
OLVER
. .............................................. 85
T
ABLA
20.
P
RUEBA DEL ESCENARIO DE TRES FACTORES PARA EL CALCULADOR
E
PANET
. ....................................................... 87
T
ABLA
21.
P
RUEBA DEL ESCENARIO DE CUATRO FACTORES PARA EL CALCULADOR
S
PARSE
S
OLVER
. ......................................... 88
T
ABLA
22.
P
RUEBA DEL ESCENARIO DE CUATRO FACTORES PARA EL CALCULADOR
E
PANET
. ................................................... 88

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
1
1. INTRODUCCIÓN Y OBJETIVOS
1.1. Introducción.
El suministro de agua potable es de vital importancia para todas las comunidades humanas; sin
embargo, en países en vías de desarrollo, como Colombia, hay todavía millones de personas que
no tienen acceso a este servicio. Dado que los recursos para construir sistemas de distribución de
agua potable son limitados, se hace indispensable contar con diseños óptimos, tanto desde el
punto de vista económico como hidráulico, para así obtener el máximo beneficio.
Identificar el diseño más eficiente y menos costoso para una red de distribución de agua potable
(RDAP) es un problema complejo. Un gran número de los tubos, deberán ser seleccionados de un
conjunto discreto de diámetros comerciales; en consecuencia, el problema se convierte en una
combinatoria enorme. Yates et al. (1984) demostraron que, en teoría, el desarrollo de un
algoritmo que pueda seleccionar diámetros discretos sobre la base de reducir al mínimo la costo
de una red de abastecimiento de agua representa un problema determinístico de matemática de
clase conocida como duro en tiempo polinomial (NP-duro). Según Templeman (1982), un
algoritmo riguroso para encontrar una combinación óptima de tuberías con diámetros discretos
no es una práctica posible debido a que el tiempo de cálculo requerido por tal algoritmo sería el
de una función exponencial del número de tuberías de la red. Por lo tanto, los métodos heurísticos
para determinar una solución cerca de la óptima son apropiados para los problemas que implican
tubos de tamaños discretos.
Varios métodos de optimización se han utilizado para encontrar una solución para el problema
planteado. Los métodos tradicionales, como la programación lineal y no lineal, no son muy
adecuados debido a que requieren que el diámetro de los tubos sea continuo, y que asumen que
las soluciones redondeadas son casi óptimas. Estos métodos a menudo llegan ya sea un óptimo
local o dejan de resolver problemas NP-duro que implican un gran número de variables (Elbeltagi,
2005). Adicionalmente, estas técnicas presentaban varios inconvenientes: eran difíciles de
implementar; usualmente llevaban a diseños con diámetros continuos, los cuales debían ser
redondeados, generando así cierto error en los resultados; no consideraban soluciones a través de
todo el espacio de búsqueda del problema, sino que realizaban búsquedas locales que podían
quedar fácilmente atrapadas en óptimos locales; la solución encontrada dependía en gran medida
del punto de partida o solución inicial considerada (Reca y Martínez, 2006). Más detalles sobre la
aplicación de estos métodos clásicos para el problema de dimensionamiento de las tuberías se
pueden encontrar en Walski (2003).
Otro tipo de técnica de optimización implica lo que es llamado un método de búsqueda adaptativa
(ASM por sus siglas en inglés). Estos métodos se basan en algoritmos computacionales extraídos
de los procesos naturales, y que han surgido como una alternativa eficaz para la solución de
problema de este tipo.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
2
Estos basan su búsqueda de la solución óptima únicamente en la evaluación de la función objetivo,
en oposición a la métodos de programación lineal y no lineal que utilizan la información del
gradiente para el mismo propósito, por lo tanto, los ASM pueden manejar fácilmente variables de
decisión discretas (Mays 1999). El Algoritmo Genético (AG) fue uno de los primeros ASM que se
introdujo (Holland, 1992), y se ha utilizado ampliamente en el diseño de redes de suministro de
agua desde su aplicación por Simpson (1994). Tratando de reducir las exigentes necesidades
computacionales de AG y evitar quedar atrapado en óptimos locales, otros ASM se han
desarrollado (Elbeltagi 2005). Por ejemplo, la optimización de colonia de hormigas (Maier, 2003),
el recocido simulado (Cunha y Sousa, 1999), la búsqueda de armonía (Geem 2006), y el algoritmo
del salto mezclado de las ranas (Eusuff y Lansey 2003) son algunos de los ASM que se han utilizado
en el diseño de sistemas de distribución de agua urbanos.
Los intentos anteriores para mejorar el rendimiento de la AG tienen centrado en el ajuste de sus
parámetros de búsqueda y funciones internas (Dandy et al 1996; Wu y Simpson 2001). Además la
mejora se podría lograr si la población inicial utilizado por el AG es estrechamente parecía la
solución óptima. Dicha población se podría producir mediante el uso de un algoritmo de
preoptimization rápido (en comparación con una GA) (Keedwell y Khu 2005 ; Kang y Lansey 2012).
Sin embargo es posible plantear una metodología para la mejora de un diseño óptimo local
obtenido como resultado del redondeo de una solución optima global en términos continuos; este
procedimiento fue planteado por Saldarriaga et al (2013). Este trabajo planeta dicha metodología
partiendo del trabajo de Manuel A. Andrade; Doosun Kang; Christopher Y. Choi; and Kevin Lansey
(2013), el cual parte de una solución de un ASM y su regla de decisión solo incluye dos parámetros
(costo y presión). La metodología parte de declaración del problema que describe cómo podría ser
alcanzado el objetivo del costo mínimo si las modificaciones adicionales en el diseño de una red se
limitaran a la reducción del diámetro de las tuberías. Entonces este trabajo, plantea la
combinación de una metodología hidráulica conocida como OPUS
1
y un algoritmo heurístico que
se utilizaron para alcanzar la mejor combinación de ajustes del diseño modificado que estaría en
más estrecha alineación con el óptimo global.
1
La metodología Optimal Power Use Surface (OPUS) se explica detalladamente en el numeral 2.7.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
3
1.2. Objetivo General.
Desarrollar una metodología que combine el algoritmo basado en hidráulica OPUS con una
metaheurística conocida como Algoritmo Voraz (Greedy Algorithm) que también contenga
parámetros hidráulicos, que permita obtener el diseño con mínimo costo constructivo que
satisfaga las restricciones hidráulicas y comerciales impuestas. Además, mediante el desarrollo de
esta metodología se pretende entender el impacto de los factores hidráulicos y económicos en la
búsqueda de los diseños óptimos, lo cual constituiría una herramienta muy útil para la
comprensión y optimización de metodologías que tengan el mismo propósito.
1.3. Objetivos Específicos.
Los objetivos específicos planteados, que permitirán lograr el objetivo general, consisten en el
análisis de metodologías actuales para el diseño de RDAP y a partir de esto formular una
metodología para la optimización del diseño de estos sistemas. Adicionalmente, los objetivos
específicos consisten en el desarrollo de toda una herramienta informática y análisis comparativos
que permitan plantear, generar y evaluar la metodología nueva para el diseño de redes de
distribución de agua potable.
Plantear el inicio en caliente (Hot Start) a partir del redondeo de una solución de OPUS.
Realizar comparaciones entre los resultados de la metodología propuesta y la metodología
de redondeo, aumento y disminución de diámetros usada en el programa REDES 2013,
para evaluar el desempeño del nuevo algoritmo de diseño que se propone.
Realizar análisis de sensibilidad del desempeño de la metodología planteada respecto a
cambios en los parámetros de entrada de la metodología.
Realizar la evaluación de la metodología planteada en diferentes casos de estudio
conocidos a nivel mundial con características topográficas y topológicas diferentes.
Desarrollar una modificación al programa informático REDES 2013 que permita al usuario
realizar el diseño mediante la metodología propuesta, presentando su correspondiente
manual de usuario y haciendo de este una herramienta fácil para el diseñador.
Presentar un análisis de los costos, número de simulaciones hidráulicas e Índice de
Resiliencia, resultante de los diferentes casos de estudio, y el efecto de los diferentes
ponderadores del Algoritmo Voraz.
Establecer el valor de los ponderadores que pueden utilizarse en la regla de decisión
planteada.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
4
2. MARCO TEÓRICO
2.1. Descripción del problema de diseño de redes de distribución de agua
potable
El problema del diseño óptimo de una RDAP se define de la siguiente manera: dado un trazado de
la red y unas demandas en los nudos de consumo, encontrar la combinación de diámetros de
tuberías que minimice el costo constructivo del sistema, satisfaciendo las restricciones de
conservación de la masa en los nudos, conservación de la energía en los circuitos y presión mínima
en los nudos de consumo, y considerando que los diámetros de las tuberías solo pueden tomar los
valores discretos que se encuentren disponibles en el mercado.
Matemáticamente, el objetivo del problema se puede expresar de la siguiente manera:
Ecuación 1
donde C es el costo constructivo de una RDAP, el cual incluye el valor comercial de las tuberías
más su costo de instalación. El costo constructivo generalmente se puede calcular mediante una
función potencial del diámetro, así:
∑
Ecuación 2
donde
: número de tubos que conforman la RDAP.
: longitud del i-ésimo tubo de la red.
: diámetro del i-ésimo tubo de la red.
y parámetros que se determinan mediante regresión teniendo en cuenta el valor comercial de
las tuberías de un material dado y su costo de instalación en función del diámetro. En múltiples
trabajos de investigación se ha determinado que el parámetro es el que más influye en el diseño
de mínimo costo que se obtenga para una red dada; este parámetro generalmente toma valores
entre 1 y 3.
En los siguientes numerales se describen las restricciones, incógnitas y ecuaciones del problema
del diseño de RDAP, a partir de lo cual se puede entender mejor su complejidad.
2.1.1. Definición del problema
Como se definió anteriormente, en el proceso de lograr un diseño óptimo de una RDAP, el objetivo
principal es encontrar la combinación de elementos (por ejemplo, diámetros de tubería y el
número y el dimensionamiento de las bombas) que minimizará una o más funciones objetivo sin
dejar de cumplir limitaciones operativas. Una problema de optimización en general, de un solo
objetivo, que tiene como objetivo minimizar el costo de construcción de las tuberías requeridas

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
5
para cualquier red de distribución dada, puede ser formalmente declarada como la combinación
de las ecuacións (1) y (2).
La restricción de presión en cada nudo se puede expresar de la siguiente manera:
Ecuación 3
donde
: valor de la restricción A en el nudo j bajo condiciones de demanda i
: mínimo admisible valor de A en la condición de la demanda i
I = número de condiciones de la demanda a analizar
J = número de nudos en la red.
Esta restricción es en general la más aplicada y por lo general se evalúa mediante la realización de
simulaciones hidráulicas de la red bajo condiciones extremas de la demanda (por ejemplo, el
caudal pico y el caudal para incendios). Sin embargo, las restricciones adicionales pueden ser
incluidas, tal como se muestra más adelante.
2.1.2. Restricciones del problema
En este estudio solo se considerarán las restricciones básicas del diseño de RDAP, que son las
restricciones hidráulicas y comerciales. Sin embargo, al diseñar una RDAP se pueden tener en
cuenta otras restricciones, tales como aquéllas relacionadas con la calidad del agua, la
confiabilidad y el impacto ambiental del sistema. Todas estas restricciones se describen a
continuación.
Restricciones hidráulicas
En el problema de diseño de RDAP existen 3 restricciones hidráulicas (Saldarriaga, 2007), estas
son: conservación de la masa en cada nudo, conservación de la energía en cada circuito y presión
igual o superior a la mínima establecida en todos los nudos y a todas las horas del día. A
continuación se explica cada una de estas restricciones.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
6
o Conservación de la masa en cada nudo:
El caudal total que entra en un nudo menos el caudal que sale de él debe ser igual al caudal
demandado en ese nudo:
∑
Ecuación 4
donde:
: número de tubos que llegan al nudo i.
: caudal que pasa por la tuberías ij hacia el nudo i desde el nudo j. De acuerdo con las
convenciones adoptadas en la práctica de la Ingeniería Hidráulica, este caudal se considera
positivo cuando va hacia el nudo i y negativo cuando sale de éste.
: caudal demandado en el nudo i.
o Conservación de la energía en cada circuito:
La suma de las pérdidas de energía en cualquier circuito debe ser igual a cero o a la energía
suministrada por una bomba si la hubiera:
∑
(
)
ó
∑
(
)
Ecuación 5
donde:
: número de tubos del circuito i.
: pérdida de energía por fricción en el tubo j del circuito i.
: pérdidas menores de energía en el tubo j del circuito i.
Existen diferentes ecuaciones para estimar las pérdidas por fricción que tienen lugar en una
tubería; las dos más utilizadas en la actualidad son la de Darcy-Weisbach y la de Hazen-Williams.
La primera es una ecuación físicamente basada, lo que implica que puede ser utilizada para
cualquier rango de condiciones físicas e hidráulicas y para cualquier fluido incompresible. En
contraste, la ecuación de Hazen-Williams es empírica y, por tanto, su aplicación está restringida a
las condiciones bajo las cuales se desarrollaron las pruebas experimentales que llevaron a su
planteamiento; éstas son:
-
El fuido debe ser agua a temperaturas “normales”.
-
El diámetro de las tuberías debe ser igual o superior a 75 mm (3 pulgadas).
-
La velocidad en las tuberías debe ser inferior a 3 m/s.
Dadas las limitaciones de la ecuación de Hazen-Williams, es preferible utilizar la ecuación de
Darcy-Weisbach. Estas dos ecuaciones para el cálculo de las pérdidas por fricción (
) se presentan
a continuación.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
7
Ecuación de Darcy-Weisbach:
Ecuación 6
donde
es la longitud del tramo de tubería en el cual se pierde
, v es la velocidad media de flujo,
es el diámetro de la tubería, g es la aceleración de la gravedad y
es el factor de fricción de
Darcy, el cual se determina mediante la ecuación de Colebrook-White:
√
(
√
)
Ecuación 7
donde
es la rugosidad absoluta de la tubería,
es el diámetro (real interno) de la tubería y
es el número de Reynolds.
Ecuación de Hazen-Williams:
Ecuación 8
donde
es el factor de conversión de unidades,
es la longitud del tramo de tubería en el cual se
pierde
,
es el caudal que fluye por la tubería,
es el coeficiente de rugosidad de la tubería,
es el diámetro (real interno) de la tubería y
y
son constantes (normalmente toman valores
de 1,852 y 4,871. respectivamente, aunque algunos diseñadores solo toman dos cifras decimales y
otros utilizan valores diferentes; estas variaciones en las constantes
y
pueden generar
diferencias significativas en los resultados obtenidos). Cuando la unidad de longitud es el pie, el
factor
toma un valor cercano a 4,727; cuando la unidad de longitud es el metro,
toma un valor
cercano a 10,667. Sin embargo, al igual que en el caso de
y
, los diseñadores utilizan diferentes
valores del factor
.
Las pérdidas menores (
) que tienen lugar en una tubería se determinan mediante la siguiente
expresión:
Ecuación 9
donde
es el coeficiente de pérdidas menores.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
8
o Presión mínima en todos los nudos de la red:
A lo largo del día se presentan variaciones en el consumo de agua y debe asegurarse que, en todo
momento, cada uno de los nudos de la red tenga una presión igual o superior a una presión
mínima dada (generalmente especificada en una norma local). Matemáticamente, esta restricción
se puede expresar de la siguiente forma:
Ecuación 10
donde
es la presión en el nudo i y
es la presión mínima requerida en el nudo i.
Restricciones comerciales
El diámetro
asignado a cada tubería i de la RDAP sólo puede tomar los valores discretos
contenidos en el conjunto de diámetros comercialmente disponibles (
):
Ecuación 11
Otras restricciones
Además de las restricciones hidráulicas y comerciales, que son esenciales, pueden incluirse otras
restricciones al momento de diseñar una RDAP; entre las más importantes y que de manera
frecuente son consideradas en el diseño se encuentran: restricciones relativas a la calidad del
agua, a la confiabilidad del sistema y al impacto ambiental.
o Restricciones relativas a la calidad del agua:
En una RDAP no basta con llevar el agua desde la fuente de abastecimiento hasta los usuarios; se
debe asegurar además que el fluido llegue con una calidad apta para el consumo humano. Las
condiciones que debe reunir el agua para que sea considerada potable están fijadas en el Decreto
1575 de 2007, el cual es desarrollado mediante la Resolución 2115 del 22 de junio de 2007. Con
respecto a la calidad del agua tratada que se pretende emplear para consumo humano, el
Numeral C.2.4. del Reglamento Técnico del Sector de Agua Potable y Saneamiento Básico de
Colombia (RAS 2000) dice lo siguiente:
“El agua para consumo humano no debe contener microorganismos
patógenos, ni sustancias tóxicas o nocivas para la salud. Por tanto, el agua
para consumo debe cumplir los requisitos de calidad microbiológicos y
fisicoquímicos exigidos en el Decreto 475 de marzo 10 de 1998, expedido por el

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
9
Ministerio de Salud o en su defecto, el que lo reemplace. La calidad del agua no
debe deteriorarse ni caer por debajo de los límites establecidos durante el
período de tiempo para el cual se diseñó el sistema de abastecimiento”.
A partir de lo anterior se puede notar que la calidad del agua es un aspecto de gran importancia en
una RDAP. Para tener una mejor calidad, existen aspectos que pueden controlarse desde el diseño
mismo de la red; algunos de éstos son:
-
Restricciones relativas a la calidad del agua: Minimizar la edad del agua o tiempo de retención
en los nudos de consumo: en general, a medida que el tiempo de retención del agua en el
sistema aumenta, su calidad se degrada, por lo cual es deseable suministrar agua “joven” (i.e.
con corto tiempo de retención) en los nudos de consumo (Committee on Public Water Supply
Distribution Systems - National Research Council of the National Academies, 2006). Dado que
la edad del agua tiene una relación estrecha con las características topológicas del sistema, es
posible orientar el diseño de una RDAP de tal manera que se minimice este variable. Para
incluir el tiempo de retención como una restricción adicional del diseño, es necesario contar
con un software de simulación hidráulica que para cada posible diseño calcule la edad del
agua en cada punto de la RDAP, además de calcular los caudales en las tuberías y las
presiones en los nudos. La edad del agua o tiempo de retención en un punto del sistema
corresponde a una mezcla de “paquetes” de agua que han viajado por caminos diferentes a lo
largo de la red hasta llegar al punto de interés; por esto, la edad del agua en un punto
determinado no es un valor único, sino que es una distribución de valores. Una manera
común de estimar el tiempo de retención en un punto dado es promediando los tiempos de
retención de todos los paquetes de agua que llegan a dicho punto.
-
Controlar las concentraciones de cloro residual libre en los nudos de consumo: uno de los
métodos de desinfección más utilizados en RDAP a nivel mundial es la cloración; de acuerdo
con el Numeral C.8.3.1.1. del RAS 2000, la cloración puede ser empleada para desinfectar las
aguas, controlar olores y sabores y prevenir el crecimiento de algas y microorganismos. Para
asegurar la eficacia de este método de desinfección sin poner en peligro la salud pública, la
concentración de cloro residual libre debe mantenerse dentro de unos límites: por ejemplo, el
Artículo 9 de la Resolución 2115 del Ministerio de la Protección Social y del Ministerio de
Ambiente, Vivienda y Desarrollo Territorial de la República de Colombia establece que el valor
aceptable del cloro residual libre en cualquier punto de la red de distribución del agua para
consumo humano deberá estar comprendido entre 0,3 mg/l y 2,0 mg/l. Así, en el diseño de
una RDAP nueva puede incluirse una restricción adicional que consista en mantener la
concentración de cloro residual libre en todos los puntos del sistema dentro de unos límites
determinados dada una concentración inicial en las fuentes de abastecimiento.
-
Controlar el desarrollo de biopelículas en las tuberías del sistema: las biopelículas son
comunidades de microorganismos de una o varias especies (e.g. hongos, algas, protozoarios)
que se encuentran rodeados por una sustancia pegajosa secretada por ellos mismos. En

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
10
general, las biopelículas pueden presentarse en cualquier superficie que entre en contacto
con el agua u otro medio líquido y su formación empieza cuando los microorganismos logran
adherirse a la superficie y empiezan a secretar sustancias limosas que se pueden pegar a
diferentes tipos de materiales (The Center for Biofilm Engineering, 2008). La presencia de
biopelícula en las paredes de las tuberías de una RDAP puede generar efectos negativos, dado
que ésta podría albergar organismos patógenos y podría eventualmente desprenderse,
afectando las propiedades organolétpicas del agua (e.g. color, turbiedad). Para controlar la
formación de biopelículas en las tuberías de las RDAP, es recomendable mantener
velocidades de flujo relativamente altas en el sistema; en caso tal que las biopelículas se
formen, un método efectivo para causar su desprendimiento es el lavado hidráulico (éste se
lleva a cabo mediante la operación de válvulas e hidrantes, con lo cual se busca obtener
velocidades de lavado que remuevan la biopelícula). Dado que la formación de biopelículas y
su remoción pueden controlarse mediante las características hidráulicas y topológicas del
sistema, es posible incluir en el problema del diseño de RDAP restricciones adicionales que
favorezcan el control de estas colonias de microorganismos.
o Restricciones relativas a la confiabilidad del sistema:
La confiabilidad es un concepto que cada vez toma más importancia en el diseño y operación de
RDAP; dado que el agua es una necesidad básica para los seres humanos, es necesario asegurar un
suministro continuo y seguro de ésta, lo que implica contar con sistemas muy confiables. Además,
si en una RDAP se presentaran con frecuencia interrupciones en el servicio, la empresa encargada
de su operación podría dejar de vender volúmenes considerables de agua, lo cual representaría
una pérdida económica importante.
Existen diferentes indicadores para cuantificar la confiabilidad de una RDAP; uno de los más
utilizados actualmente por los investigadores a nivel mundial es el Índice de Resiliencia -I
r
- (Todini,
2000). El creador de este índice, Ezio Todini, lo define de la siguiente manera (Todini, 2008):
“La resiliencia es la capacidad intrínseca que tiene una RDAP para
superar fallas repentinas y se mide como la proporción entre el
excedente de potencia que es entregado a los usuarios y la máxima
potencia que puede ser disipada en la red cuando se cumplen
exactamente los criterios y condiciones de diseño. El Índice de
Resiliencia proporciona una medida general de la redundancia del
sistema: un mayor valor del Índice de Resiliencia corresponde a una
mayor redundancia.”
De acuerdo con lo anterior, el I
r
es un indicador de la vulnerabilidad de la red frente a la posibilidad
de dejar ciertos nudos del sistema sin servicio en caso de ocurrir una falla. Este índice se
fundamenta en la relación existente entre la resiliencia de un sistema y la cantidad de energía que
éste disipa; a menor energía disipada, mayor será la capacidad de respuesta del mismo debido a
que tiene mayor cantidad de energía disponible.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
11
Por otro lado, Tricarico et al. (2008) definieron la confiabilidad de una RDAP como la probabilidad
de que simultáneamente se satisfaga la restricción de presión mínima en todos los nudos de la red
(considerando diferentes condiciones de operación, consumo y otras eventualidades).
Según sea el caso, el diseñador podrá elegir o incluso definir el indicador de confiabilidad que
mejor se ajuste a sus necesidades y podrá incluirlo dentro del diseño de la RDAP. En general, la
manera en la que se han incluido los indicadores de confiabilidad dentro del diseño de RDAP ha
sido considerándolos como un objetivo adicional al objetivo del costo mínimo. Por ejemplo, Todini
(2000) desarrolló una metodología de diseño que consiste en encontrar el frente óptimo de Pareto
considerando dos objetivos: la maximización del Índice de Resiliencia y la minimización de los
costos.
o Restricciones relativas a la confiabilidad del sistema:
El consumo de agua por parte de los seres humanos tiene, por sí mismo, un impacto ambiental
importante: el agua que es consumida debe ser abstraída de cuerpos de agua, lo cual puede
afectar el equilibrio de los ecosistemas. Si esta abstracción se hace de manera intensiva,
superando la capacidad de producción hídrica del ecosistema circundante, se puede poner en
peligro la vida de los individuos que lo habitan. Considerando los siguientes tres factores, se puede
ver que la situación planteada es cada vez más preocupante: 1) el acelerado crecimiento
poblacional que se ha producido en las últimas décadas, lo cual hace que incremente el consumo
de agua; 2) el calentamiento global; 3) la creciente contaminación de los cuerpos de agua, lo que
reduce las fuentes hídricas aptas para el consumo humano.
Si al consumo de agua se sumaran las pérdidas por fugas en el sistema, el volumen total de agua
abstraído de los cuerpos hídricos aumentaría. Esto podría tener impactos ambientales graves; por
ejemplo, podría llevar a una reducción importante en el caudal de los ríos o a un descenso del
nivel freático superior al que se tendría si no existieran fugas (Engelhardt et al., 2000). Dado que el
caudal de fugas es proporcional a la presión, se ha determinado que es posible disminuir las
pérdidas de agua debidas a fugas mediante la reducción y uniformización de las presiones en los
nudos del sistema (Araque y Saldarriaga, 2006). Así, otro criterio o restricción que se podría incluir
dentro del diseño de una RDAP es la minimización del caudal de fugas, lo cual se puede lograr
reduciendo presiones y minimizando la desviación estándar de la variación espacial de las
presiones en la red (i.e. hacer más uniformes las presiones de la RDAP).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
12
2.2. Incógnitas y ecuaciones del problema
Como se explicó anteriormente, lo que se busca en el diseño de una RDAP es determinar el
diámetro de cada una de las tuberías que conforma el sistema, a partir de lo cual se puede
conocer la presión en cada nudo y el caudal en cada tubería. Así pues, las incógnitas que se tienen
son: diámetro y caudal de cada tubería y presión en cada nudo. Si NT corresponde al número de
tuberías del sistema y NU al número de uniones o nudos, el total de incógnitas es: NT + NT + NU.
En cuanto a las ecuaciones disponibles, se tiene que por cada circuito se puede plantear una
ecuación de conservación de energía como la Ecuación 4; si en ésta se sustituye la ecuación de
Darcy-Weisbach (Ecuación 6) para el cálculo de las pérdidas por fricción y la expresión de las
pérdidas menores (Ecuación 9) como función de la altura de velocidad, se obtiene la siguiente
expresión:
∑
(∑
)
Ecuación 12
donde:
: número de tubos del circuito i.
: caudal que fluye por el tubo j del circuito i.
: área transversal interna del tubo j del circuito i.
: coeficiente de pérdidas menores del tubo j del circuito i.
: factor de fricción del tubo j del circuito i.
: longitud del tubo j del circuito i.
: diámetro del tubo j del circuito i.
La Ecuación 12 es no lineal y se conoce como ecuación de caudal; en una RDAP se tienen NC
ecuaciones de este tipo, donde NC corresponde al número de circuitos cerrados que hay en el
sistema.
Por otra parte, en cada nudo se puede plantear la ecuación de conservación de la masa (Ecuación
3); si para cada uno de los caudales
: involucrados en esta ecuación se plantea la ecuación de
conservación de la energía entre sus nudos inicial y final (i.e. nudos i y j), incluyendo las pérdidas
por fricción (calculadas con la ecuación de Darcy-Weisbach) y las pérdidas menores, es posible
despejar el caudal y obtener la siguiente expresión:

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
13
√
(∑
)
⁄
(|
|)
⁄
Ecuación 13
Las ecuaciones de este tipo son también no lineales y se conocen como ecuaciones de altura
piezométrica; en una RDAP se tienen (NU – 1) ecuaciones de éstas, siendo necesario conocer la
altura piezométrica de algún nudo de la red (generalmente se conoce la altura del embalse o
fuente de abastecimiento) para solucionar este conjunto de ecuaciones.
Finalmente, se tiene un total de NC + (NU – 1) ecuaciones disponibles. Además, es fácil demostrar
que, para cualquier RDAP, este número de ecuaciones es igual al número de tubos (NT) que la
conforman, es decir: NC + (NU - 1) = NT.
Se puede ver que el número de incógnitas (2NT + NU) excede en más del doble al número de
ecuaciones disponibles (NT).
2.3. Complejidad del problema
Teniendo en cuenta que:
a) el número de incógnitas excede en más del doble al número de ecuaciones disponibles,
b) la relación entre las pérdidas de energía que tienen lugar en una tubería y el caudal que
fluye por éstas es no lineal (Ecuaciones 11 y 12),
c) las variables de decisión del problema (i.e. los diámetros de las tuberías) sólo pueden
tomar valores discretos (Ecuación 10),
se puede concluir que el diseño de una RDAP nueva es un problema bastante complejo que ha
sido definido como un problema combinatorio NP-DURO (Yates et al. 1984), lo que quiere decir
que no se conoce un método determinístico para solucionarlo en un tiempo polinomial
2
. Por esto,
el diseño optimizado de RDAP no puede ser tratado de forma convencional, sino que su solución
requiere de metodologías especiales que, en un tiempo computacional razonable, permitan
obtener la configuración de mínimo costo que satisfaga las restricciones hidráulicas, comerciales y
otras adicionales que el diseñador desee establecer.
2
Un algoritmo de tiempo polinomial es aquél cuyo tiempo de ejecución (el número de operaciones de bits
elementales hechas en una cadena de entrada de longitud N) está acotado por un polinomio p(N) (Villalba,
2004).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
14
2.4. Aproximaciones al problema del diseño de redes de distribución de
agua potable
2.4.1. Aproximación tradicional al problema del diseño de RDAP
Tradicionalmente y de manera especial en países en desarrollo, el problema del diseño de RDAP se
ha resuelto por ensayo y error, orientado por la experiencia del diseñador y por reglas locales
establecidas por los organismos encargados del manejo del agua potable. Generalmente, estas
reglas locales establecen los diámetros mínimos que deben utilizarse según se trate de líneas
primarias, secundarias o de distribución; el espaciamiento máximo entre los cruces de tuberías;
velocidades máximas; longitudes máximas de tuberías dependiendo de si éstas terminan en un
punto ciego o si se encuentran conectadas en los dos extremos; entre otros aspectos.
Lo que comúnmente hacen los diseñadores es determinar el trazado o distribución geométrica de
la red, desagregar los caudales en las diferentes subáreas de la ciudad y concentrar estos caudales
desagregados en los nudos del sistema. Una vez se han definido las demandas de caudal y la
topología de la red (excepto los diámetros de las tuberías), el diseñador asigna a cada tubería un
diámetro inicial según los criterios contenidos en las normas locales y, utilizando un motor de
cálculo hidráulico (e.g. EPANET), calcula los caudales resultantes en cada tubo y las presiones en
cada nudo para la configuración de diámetros inicialmente seleccionada. Posteriormente, el
diseñador compara las velocidades y presiones obtenidas con las establecidas en la norma y va
ajustando los diámetros de las tuberías hasta obtener una solución que satisfaga los criterios de
velocidad y presión señalados en la norma. De este modo se obtienen diseños funcionales que
logran llevar el agua desde la fuente de abastecimiento hasta los usuarios, pero que se alejan
considerablemente del diseño de mínimo costo.
Un punto de la metodología tradicional de diseño de RDAP que vale la pena resaltar corresponde a
las velocidades máximas admisibles en las tuberías; en la actualidad, se cuenta con materiales muy
resistentes y con métodos de análisis y herramientas computacionales que permiten conocer las
sobrepresiones que un fenómeno transiente (e.g. golpe de ariete) puede generar en los diferentes
puntos de la red, de tal modo que se puede determinar si las tuberías pueden o no soportar los
esfuerzos a los que van a estar sometidas. Es por esto que limitar las velocidades en las tuberías no
es justificable y, en cambio, sí es una de las principales causas para tener tuberías con grandes
diámetros en la red, lo cual eleva considerablemente los costos y puede generar problemas de
calidad del agua debido al mayor tiempo de retención del fluido en el sistema.
A partir de los puntos expuestos, se puede concluir que la aproximación tradicional al problema
del diseño de RDAP lleva a configuraciones hidráulicamente ineficientes y bastante alejadas del
diseño de costo mínimo. Teniendo en cuenta que los recursos disponibles para la construcción y
operación de RDAP son limitados, se hace evidente la necesidad de abandonar las metodologías
de diseño tradicionales y adoptar metodologías modernas que optimicen el problema y permitan
obtener diseños eficientes y de mínimo costo. Si además de encontrar diseños óptimos, las
metodologías permitieran comprender los factores que afectan dichos diseños, se tendría una
herramienta supremamente útil para el análisis y la optimización de redes existentes.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
15
2.5. Metodologías de diseño optimizado de RDAP desarrolladas
recientemente a nivel mundial
El problema del diseño optimizado de RDAP ha despertado el interés de muchos investigadores
alrededor del mundo en las últimas décadas, llevando al desarrollo de diferentes metodologías
para solucionarlo. La mayoría de estas metodologías parten de una solución inicial y utilizan
técnicas determinísticas de búsqueda para pasar de una solución a otra hasta que no se logre una
reducción adicional en el costo de la red. A continuación se describen algunas de las metodologías
de diseño optimizado más estudiadas y aplicadas en los últimos años a nivel mundial; como se
verá, éstas se basan en la simulación de fenómenos naturales o artificiales, a diferencia de OPUS
que utiliza las características hidráulicas del sistema para encontrar el diseño de costo mínimo.
2.5.1. Algoritmos genéticos
Los Algoritmos Genéticos (AG) son un método de búsqueda aleatoria utilizado para resolver
problemas de optimización. Aunque por ser aleatorios los AG no garantizan encontrar el mínimo
global, su aplicación al problema del diseño óptimo de RDAP ha sido exitosa, logrando encontrar
diseños de bajo costo después de un número razonable de generaciones.
Los AG son un tipo particular de Algoritmos Evolutivos, los cuales utilizan técnicas inspiradas en la
evolución biológica de las especies, tales como herencia, mutación, recombinación genética y
selección natural. Estos algoritmos son implementados de tal manera que la población de
individuos que constituyen las posibles soluciones al problema evolucione hacia mejores
soluciones. En el caso del diseño de RDAP, cualquier individuo i tiene especificado el diámetro de
cada una de sus NT tuberías, los cuales pueden almacenarse en un vector de valores discretos NT;
este vector representa el genotipo de la red bajo diseño (Saldarriaga, 2007). El fenotipo de cada
individuo corresponde a la presión en cada una de las NU uniones de la red, la cual se determina
utilizando un motor de cálculo hidráulico y se codifica en un vector NU. Habitualmente, la primera
generación de individuos se genera de manera aleatoria y a partir de ésta se producen
sucesivamente nuevas generaciones mediante las técnicas de evolución mencionadas. En cada
generación se evalúa el desempeño o aptitud de cada uno de los individuos que la conforman;
esto se hace mediante una función de costos similar a la Ecuación 2. Dado que lo que se busca en
el diseño de RDAP es minimizar el costo del sistema, los individuos más aptos serán los de menor
costo. Al evaluar el desempeño de los individuos de cada generación, se seleccionan los individuos
más aptos y éstos son comparados con los mejores individuos de generaciones pasadas para elegir
los “nuevos mejores individuos”. Adicionalmente, con base en la aptitud o desempeño de los
individuos de cada generación, algunos de ellos son seleccionados de manera estocástica y son
modificados (mediante operadores como mutación y recombinación) para dar origen a una nueva
generación. En general, siguiendo la teoría de la selección natural, los individuos más aptos son los
que tienen mayor probabilidad de reproducirse y de pasar sus genes a generaciones siguientes; sin
embargo, para evitar quedar atrapado en un mínimo local, es necesario introducir cierta variación
en el genotipo de las generaciones siguientes. Este procedimiento se repite para cada generación
y la solución al problema está dada por los mejores individuos de entre todas las generaciones.
Usualmente, el algoritmo termina cuando se alcanza un número dado de generaciones, cuando se

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
16
ha alcanzado un nivel de aptitud o costo determinado, o cuando se deja observar mejoría en
generaciones siguientes.
Cabe anotar que los AG no manejan de manera independiente las restricciones hidráulicas del
problema, pero éstas pueden tenerse en cuenta incluyendo un término de penalización en la
función de costos (Goldberg, 1989), el cual aumente el costo de un individuo particular cuando se
viole la restricción de mínima presión en los nudos. De este modo, cuando un posible diseño no
satisfaga las restricciones hidráulicas del problema, el término de penalización hará que su costo
sea muy elevado, convirtiéndolo en un individuo poco apto que seguramente quedará por fuera
del espacio factible de solución.
La eficiencia y eficacia de los AG depende de múltiples parámetros, entre los que se encuentra la
forma de codificación utilizada. Tradicionalmente, las soluciones de los AG son representadas
mediante cadenas binarias de 0s y 1s, aunque es posible utilizar otras formas de codificación. Por
ejemplo, Dandy et al. (1996) y Savic y Walters (1997) encontraron que la codificación gris (gray
coding) resulta mejor que la codificación binaria. En 2000, Vairavamoorthy y Ali propusieron
utilizar una “cadena real codificada” (real coded string), la cual no requiere ser codificada y
decodificada, logrando así una reducción en el tiempo computacional. También con el propósito
de mejorar la eficiencia y eficacia de los AG, se han propuesto modificaciones a las funciones de
costos y penalización y al proceso de selección (e.g. Savic y Walters, 1997); a los operadores de
mutación y recombinación (e.g. Goldberg, 1989; Villalba, 2004); reducciones del espacio de
búsqueda (e.g. Kadu et al., 2008), entre otras tácticas.
2.5.2. Búsqueda de Armonía (Harmony Search)
La Búsqueda de Armonía imita el proceso de improvisación de los músicos (especialmente la
improvisación en el jazz) con el propósito de encontrar la mejor solución a un problema de
optimización; en este caso, el propósito es encontrar el diseño de mínimo costo. En el proceso de
improvisación, cada músico toca una nota buscando obtener un perfecto estado de armonía
conjunta (armonía fantástica). De manera análoga, en el caso del diseño de RDAP se busca el
conjunto de diámetros que permita obtener la mejor solución conjunta, es decir, que minimice
una función de costos determinada.
De la misma manera en la que en el jazz el estado de “armonía fantástica” se determina mediante
una apreciación estética, en el diseño de RDAP el mejor estado u óptimo global se determina
mediante la evaluación de una función de costos. La apreciación estética está dada por el conjunto
de tonos tocados por cada instrumento; análogamente, la evaluación de la función de costos está
dada por el conjunto de valores asignados a las variables de decisión (i.e. a los diámetros de las
tuberías). En la improvisación musical, la calidad de la armonía se mejora ensayo tras ensayo, de la
misma forma en que la calidad de la solución al problema del diseño se mejora iteración tras
iteración. Para ilustrar este proceso, se puede analizar el siguiente ejemplo (Geem, 2006): se tiene
un trío de jazz compuesto por un saxofón, un bajo y una guitarra. En la memoria de cada músico
existe un cierto número de tonos preferidos: saxofonista {Do, Mi, Sol}, bajista {Si, Sol, Re} y
guitarrista {La, Fa, Do}. Si el saxofonista toca un Sol, el bajista un Si y el guitarrista un Do, juntos

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
17
conforman una nueva armonía {Sol, Si, Do}, la cual corresponde al acorde C
7
. Si esta nueva
armonía es mejor que la peor armonía que tenían los músicos en su memoria, la nueva armonía es
incluida en sus memorias y la peor es eliminada. Este procedimiento se repite hasta encontrar la
armonía perfecta.
Los parámetros del algoritmo de búsqueda de armonía son: tamaño de la memoria, tasa de
selección de la memoria, tasa de ajuste de los tonos y ancho de banda o magnitud del cambio que
se debe llevar a cabo para hacer un ajuste de tono. A medida que la búsqueda avanza, es posible
variar los parámetros del algoritmo para obtener mejores resultados.
En 2006, Geem utilizó el algoritmo de búsqueda de armonía para encontrar el diseño óptimo de
cinco RDAP y obtuvo soluciones de igual o menor costo que las obtenidas mediante otros
algoritmos metaheurísticos como los AG, el Recocido Simulado y la Búsqueda Tabú.
Posteriormente, en 2009, Geem fusionó la técnica de Búsqueda de Armonía con otra técnica
llamada Enjambre de Partículas; con esta combinación logró encontrar diseños de mínimo costo
en muy pocas iteraciones.
2.5.3. Recocido Simulado (Simulated Annealing)
El Recocido Simulado es un algoritmo para la optimización de problemas cuyo espacio de
búsqueda es muy grande. En general, este algoritmo se aplica cuando el conjunto de posibles
soluciones está conformado por variables discretas, es decir, cuando se presentan problemas
combinatorios, como es el caso del diseño de RDAP.
El nombre y la estructura de este algoritmo están basados en la técnica de recocido que se utiliza
en metalurgia, la cual consiste en calentar y enfriar de manera controlada un material con el
propósito de incrementar el tamaño de sus cristales y reducir sus defectos. Al calentar el material,
sus átomos son “liberados” de su posición inicial y adquieren movilidad, lo que les permite
alcanzar diferentes estados. Si el material se enfría de manera apropiada, sus átomos alcanzarán el
estado de mínima energía, lo cual corresponde a una estructura cristalina ordenada (Cunha y
Sousa, 1999). Hace aproximadamente 25 años, el algoritmo del Recocido Simulado fue utilizado
con éxito por Kirkpatrick, Gellatt y Vecchi (1983) y por Černý (1985) para la solución del típico
problema de optimización combinatoria denominado “el problema del vendedor viajero” y desde
entonces se ha aplicado de manera exitosa a la solución de múltiples problemas de optimización
en ingeniería. Este método es la adaptación del algoritmo Metropolis-Hastings desarrollado por N.
Metropolis en 1953.
De manera análoga al proceso físico del recocido, en cada paso del algoritmo la solución actual es
reemplazada por una nueva solución; esta última es elegida en la vecindad de la configuración
actual de manera aleatoria o con una probabilidad de escogencia que depende de los valores que
conforman la actual solución y de un parámetro global T (temperatura) que es disminuido
gradualmente durante el proceso. En cada iteración, la nueva configuración es evaluada para
determinar si se acepta o no; si es aceptada, se convierte en el punto de partida de la siguiente
iteración; de lo contrario, la configuración inicial será nuevamente el punto de partida. Cuando el
parámetro T toma valores grandes, la selección de la nueva configuración es casi aleatoria; a

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
18
medida que T disminuye la selección es más “dirigida”. Eventualmente, el algoritmo permite
incrementar el valor de T con el propósito no quedar atrapado en mínimos locales. Si durante el
proceso completo el valor del parámetro T se disminuye a la tasa apropiada, el sistema tenderá a
converger a la configuración global de mínimo costo. En 1999, Cunha y Sousa aplicaron por
primera vez la técnica de recocido simulado al diseño de RDAP; al comparar los diseños obtenidos
con los encontrados por otros autores mediante diferentes metodologías de optimización,
probaron la utilidad de esta técnica para la optimización del diseño de RDAP. En años recientes,
otros autores (e.g. Tospornsampan et al., 2007a; Reca et al., 2007) han aplicado con éxito la
técnica del recocido simulado al diseño optimizado de RDAP.
2.5.4. Búsqueda Tabú (Tabu Search)
La Búsqueda Tabú es una técnica heurística que puede utilizarse para la solución de problemas de
optimización combinatoria. Ésta fue desarrollada por Fred Glover en 1997 y se basa en el proceso
de memoria humana y en la exploración de la vecindad de la solución posible x que se esté
analizando en un momento determinado para moverse iterativamente desde esta solución hacia
una solución x’ que se encuentra en la vecindad de x. Al implementar el algoritmo, es necesario
crear un mecanismo especial para explorar la vecindad de la solución actual; este mecanismo
define los movimientos que se realizan en cada iteración. En este algoritmo, la estructura de
memoria denominada “lista tabú” es utilizada para evitar visitar de manera repetida soluciones
que han sido analizadas previamente. La lista tabú es una memoria de corto plazo que contiene las
soluciones que han sido visitadas en el pasado reciente (hace menos de n iteraciones, donde n es
el número de soluciones previas almacenadas en la memoria); así, cuando el proceso de búsqueda
trata de ir hacia soluciones recientemente visitadas, el movimiento es prohibido y se denomina
“movimiento tabú”. De acuerdo con el valor del parámetro n, los movimientos tabú permanecerán
por más o menos tiempo (i.e. más o menos número de iteraciones) en la lista tabú.
Por otro lado, existe una variación de la lista tabú que prohíbe soluciones que contengan ciertos
atributos; así, algunos atributos de las soluciones recientemente visitadas son marcados como
“tabú - activos” y las posibles soluciones que contengan elementos de este tipo ganarán el estado
de tabú. Cuando sólo unos atributos son marcados como tabú-activos, generalmente son varias las
soluciones que resultan marcadas como tabú, lo que lleva a su exclusión de la búsqueda. Sin
embargo, puede ocurrir que algunas de las soluciones marcadas como tabú (debido a los atributos
tabú-activos) sean de excelente calidad; para superar este problema se utilizan los “criterios de
aspiración”, los cuales permiten, en casos particulares, modificar el estado de tabú de una solución
admitiendo así su inclusión en el conjunto de soluciones permitidas.
En 2004, Cunha y Ribeiro aplicaron la Búsqueda Tabú al diseño de algunas RDAP de prueba que
son utilizadas a nivel mundial y cuyos diseños optimizados son reportados en la literatura; los
resultados demostraron que el algoritmo de Búsqueda Tabú es útil para resolver el problema del
diseño optimizado de RDAP. Posteriormente, Tospornsampan et al (2007) y Reca et al. (2007)
aplicaron de nuevo la Búsqueda Tabú al problema mencionado.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
19
2.5.5. Criterio geométrico de diseño propuesto por I Pai Wu
En 1975, el ingeniero I-pai Wu desarrolló un criterio para el diseño de sistemas de riego a presión,
el cual ha probado ser útil para obtener el diseño de costo mínimo de tuberías en serie con
distribución uniforme de las demandas.
Este criterio se basa en determinar la forma de la línea de gradiente hidráulico (LGH) óptima, es
decir, la LGH correspondiente al diseño de mínimo costo. Si en una serie de tuberías se conoce de
antemano la forma de la LGH óptima, es posible determinar las pérdidas de energía que se
deberían producir en cada tramo para tener el diseño de mínimo costo. Conociendo el caudal (el
cual se puede determinar con facilidad en una serie de tuberías) y las pérdidas ideales en cada
tramo, se puede estimar el diámetro requerido utilizando una ecuación de resistencia como la de
Hazen-Williams o la de Darcy-Weisbach; así, el problema del diseño de series de tuberías se
convierte en un conjunto de diseños de tuberías simples.
Con el propósito de encontrar la forma de la LGH óptima, I-pai Wu analizó series de tuberías con
demandas uniformes (igualmente espaciadas y de igual magnitud) y con topografía variada (que
incluyen pendientes ascendentes y descendentes, tanto uniformes como no uniformes); en estas
series Wu probó 15 patrones de LGH diferentes. Además, utilizó una ecuación potencial de costos
como la Ecuación 2 y llevó a cabo múltiples simulaciones para valores del exponente de costos b
entre 1 y 3.
A partir de los resultados obtenidos, Wu determinó que la serie de tuberías de menor costo
(considerando solo costos de materiales y construcción) corresponde a aquella cuya LGH forma
una curva cóncava hacia arriba que se encuentra un poco por debajo de la línea recta que une las
alturas de energía total al inicio (Punto A de la Figura 1) y al final (Punto B de la Figura 1) de la serie
de tuberías. De manera más exacta, Wu estableció que la LGH óptima tiene, en la sección media
de la serie de tuberías, una flecha del 15% de ΔH con respecto a la línea recta (línea AB de la Figura
1) previamente descrita, donde ΔH corresponde a la altura total disponible (
). Esto se ilustra en la Figura 1.
Figura 1 Criterio de I-pai Wu. (Ochoa, 2009)

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
20
Por otra parte, I-pai Wu demostró que si se utilizara una LGH recta para diseñar (línea AB de la
Figura 1), solo se produciría un incremento de 2,5% o menos en los costos con respecto al diseño
óptimo. Asimismo, Wu descubrió que todas las LGH que estuvieran por encima de la LGH recta
llevarían a diseños más costosos que los correspondientes a la configuración que genere una LGH
recta.
Cabe anotar que los diámetros obtenidos al aplicar el criterio de I-pai Wu son diámetros continuos
y es necesario aproximarlos a un diámetro comercial, con lo cual los costos iniciales de materiales
y construcción podrían variar.
Se puede entonces observar que, a diferencia de las metodologías de diseño descritas en el
Numeral 3.2, el criterio de I-pai Wu se basa en características geométricas e hidráulicas del
sistema para encontrar el diseño óptimo. Sin embargo, este criterio tiene la limitación de sólo ser
aplicable al diseño de tuberías en serie con demandas aproximadamente uniformes.
Aplicación del criterio de I Pai Wu al caso de RDAP
Criterio de featherstone (1983)
3
En 1983, el profesor Ronald Featherstone, de la Universidad de Newcastle upon Tyne, propuso
extender el criterio de I-pai Wu al caso de RDAP; con base en esta idea, estableció la metodología
que se describe a continuación para alcanzar el diseño óptimo de RDAP.
El procedimiento planteado por Featherstone consiste en calcular unas alturas piezométricas
ideales en cada uno de los nudos de la red. Para esto se establece un plano inclinado de presiones
cuyo punto más alto corresponde al tanque de abastecimiento o estación de bombeo y su punto
más bajo es la altura piezométrica del nudo más alejado del tanque (que debe tener la altura
piezométrica mínima); así, al conocer la forma del plano, se procede a calcular la altura
piezométrica ideal en cada nudo, de tal modo que ésta quede ubicada sobre el plano inclinado
descrito previamente (Saldarriaga, 2001). Este concepto se ilustra en la Figura 2.
3
Tomado de:
Saldarriaga, J. G., 2007. Hidráulica de Tuberías: abastecimiento de agua, redes, riegos. Editorial Alfaomega.
Bogotá, Colombia.
Villalba, G., 2004. Algoritmos de optimización combinatoria aplicados al diseño de redes de distribución de
agua potable. Tesis de magíster. Universidad de los Andes, Bogotá, Colombia.
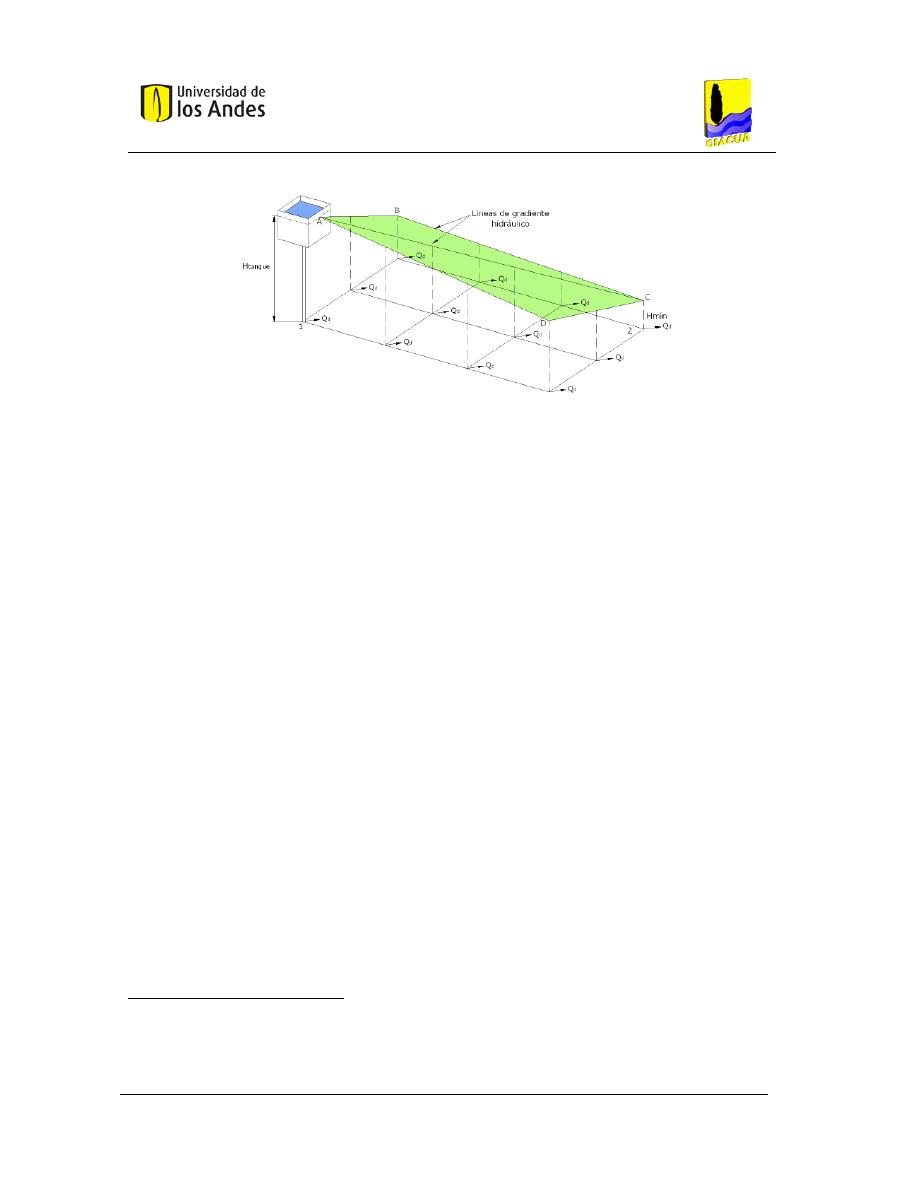
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
21
Figura 2 Criterio de I-pai Wu. Ochoa (2009)
En la Figura 2 los planos ABC y ADC deben formar parte de un mismo plano general; las líneas
punteadas corresponden a las alturas piezométricas de cada uno de los nudos de la red; el punto 2
corresponde al nudo más alejado y, por lo tanto, al de mínima presión; y el punto 1 corresponde al
tanque de abastecimiento.
En general, el criterio de Featherstone funciona bien en redes planas, cuadriculadas y con un solo
tanque de abastecimiento y puede presentar problemas cuando la topografía es variada, la
topología compleja, cuando aumenta el número de tanques de abastecimiento o cuando existen
bombeos directos a la red.
2.5.6. Superficie óptima de presiones (SOP, villalba, 2004)
4
El método de diseño por Superficie Óptima de Presiones (SOP) fue desarrollado por Germán
Villalba en 2004 como su tesis de Maestría en Ingeniería de Sistemas de la Universidad de los
Andes.
Esta metodología es una extensión del criterio de I-pai Wu al caso de RDAP; además, dado que es
aplicable a redes de distribución con cualquier topología y topografía, constituye una mejora al
método propuesto por Featherstone.
La idea central de la metodología SOP es suponer que existe una superficie ideal de presiones
conformada por una serie de puntos (X, Y, h), en donde X y Y representan las coordenadas planas
de cada nudo de la red y h representa la altura piezométrica en éstos; con estas alturas ideales en
los nudos de la red se pretende obtener una configuración de diámetros que tenga un costo muy
cercano al mínimo.
4
Tomado de:
Saldarriaga, J. G., 2007. Hidráulica de Tuberías. Editorial Alfaomega. Bogotá, Colombia.
Villalba, G., 2004. Algoritmos de optimización combinatoria aplicados al diseño de redes de distribución de
agua potable. Tesis de magíster. Universidad de los Andes, Bogotá, Colombia.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
22
Para calcular la superficie óptima de alturas piezométricas es necesario definir cuatro elementos:
1) la LGH en cada una de las fuentes de abastecimiento de la red; 2) la presión mínima requerida
en los nudos; 3) la distancia de cada nudo de consumo a las fuentes de abastecimiento; 4) una
ecuación que modele la caída de la altura piezométrica de nudo a nudo (partiendo de la fuente de
abastecimiento hasta llegar al nudo más alejado). Los dos primeros elementos se pueden conocer
con facilidad: la LGH de las fuentes de abastecimiento está dada por su localización con respecto a
la red y por las reglas de operación del sistema, en tanto que la presión mínima requerida en los
nudos está normalmente fijada en una norma local. En contraste, existen diferentes formas de
calcular la distancia de los nudos de consumo a las fuentes de abastecimiento y de modelar la
caída de la altura piezométrica; éstas se describen a continuación:
Cálculo de las distancias a las fuentes
La distancia entre un nudo cualquiera de la red con coordenadas (X, Y, Z), donde Z corresponde a
la cota física del nudo, y una de las fuentes de abastecimiento del sistema se puede calcular de
tres maneras:
-
Distancia euclídea 2D: La distancia euclídea en dos dimensiones corresponde a la distancia
entre dos puntos considerando solamente sus coordenadas planas X y Y.
-
Distancia euclídea 3D: La distancia euclídea en tres dimensiones corresponde a la
distancia entre dos puntos teniendo en cuenta sus coordenadas X, Y y Z.
-
Distancia topológica: La distancia topológica entre dos puntos de una RDAP corresponde a
la mínima distancia o recorrido para llegar de un punto al otro a través de las tuberías del
sistema; esta distancia depende entonces de la topología de la red y del sentido de flujo
en las tuberías, el cual determina la ruta que sigue el agua para llegar a un punto
determinado del sistema. Para calcular la distancia topológica no es suficiente una
ecuación, sino que es necesario implementar un algoritmo que determine la distancia
mínima entre dos vértices de un grafo; en este caso, un vértice sería la fuente y el otro el
nudo i.
Para el cálculo de la Superficie Óptima de Presiones se debe utilizar la distancia topológica, dado
que es la distancia que representa el recorrido real del agua en la red y, por lo tanto, es
proporcional a las pérdidas de energía en la misma.
Ecuaciones para modelar la caída de la altura piezométrica ideal de nudo a nudo
En su tesis, Germán Villalba probó diferentes ecuaciones que permiten determinar las superficies
óptimas de presiones para una red con una o varias fuentes de abastecimiento. Las ecuaciones
probadas por Villalba para modelar la caída de altura piezométrica fueron:
-
Ecuación lineal: Esta ecuación modela una relación lineal entre la LGH ideal y la distancia
entre los nudos y las fuentes.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
23
-
Ecuación cuadrática: Esta ecuación establece una relación cuadrática entre la LGH ideal y
la distancia entre los nudos y las fuentes.
-
Ecuación catenaria: Esta ecuación establece la relación entre la LGH ideal y la distancia
entre los nudos y las fuentes mediante una curva catenaria.
-
Ecuación recíproca: Esta ecuación modela la relación entre la LGH ideal y la distancia entre
los nudos y las fuentes como una curva recíproca.
2.5.7. Metodología de superficie óptima de gradiente hidráulico (SOGH)
Esta metodología corresponde a la expansión a RDAP de la metodología desarrollada para el
diseño de series de tuberías (Numeral 4.3.3), la cual se basa determinar la forma de la LGH óptima
de un sistema de distribución y a partir de ésta calcular los diámetros de las tuberías que generan
tal LGH y que conforman un diseño cercano al de mínimo costo. La nueva metodología es similar a
la metodología SOP (Numeral 3.4.2), pero tiene dos rasgos nuevos y diferentes:
1) Para cada sistema de distribución se estima la flecha máxima óptima de la curva
LGH vs. Abscisa, la cual es función de la distribución de demandas, el caudal total,
la longitud total de tuberías y la función de costos. En contraste, en la metodología
SOP se supone que la flecha óptima para todas las RDAP es el 15% de la altura
piezométrica disponible (H) y no se tiene en cuenta la variación de dicha flecha
con las características hidráulicas, topológicas y comerciales del sistema.
2) Al implementar el algoritmo para el cálculo de la superficie óptima de gradiente
hidráulico se corrigieron los errores de la metodología SOP descritos en el
Numeral 3.4.2.4, de tal modo que la nueva metodología es aplicable a redes con
cualquier topología, topografía variable y múltiples fuentes de abastecimiento.
Además, el resultado que se obtiene con la metodología SOGH no está
condicionado por el diseño inicial o “semilla” de la red.
Esta nueva metodología fue implementada en el software de simulación hidráulica y diseño REDES
(CIACUA, 2008), el cual ofrece una interfaz cómoda para trabajar y, además, cuenta con múltiples
funciones y procedimientos que hicieron más fácil y ágil la implementación de la metodología
propuesta.
Las etapas que conforman la metodología de la Superficie Óptima de Gradiente Hidráulico (SOGH)
se enuncian a continuación. Es importante anotar que antes de aplicar esta metodología se deben
fijar los parámetros de diseño tales como: presión mínima requerida (P
mín
), función de costos, base
de diámetros comerciales disponibles, ecuación de pérdidas de energía por fricción (Darcy-
Weisbach o Hazen-Williams), número máximo de iteraciones y error admisible en el cálculo de la
superficie óptima de gradiente hidráulico, entre otros.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
24
Etapas que conforman la metodología SOGH:
Cada una de las etapas que se enuncia a continuación corresponde a un proceso complejo
compuesto por múltiples actividades; es por eso que a éstas se les denomina “etapas” y a las
actividades que las conforman se les denomina “pasos”.
1. Asignación inicial de diámetros proporcionales a la distancia topológica.
2. Estimación de la flecha óptima de la curva LGH vs. Abscisa.
3. Con la asignación de diámetros actual, realizar una simulación hidráulica para determinar
caudales, sentidos de flujo en las tuberías y calcular las distancias topológicas de los nudos a
las fuentes de abastecimiento.
4. Cálculo de la superficie óptima de gradiente hidráulico; es decir, estimación de la LGH ideal de
cada nudo de la red. Este cálculo se hace con base en las distancias topológicas calculadas
previamente.
5. Asignación de las pérdidas de energía objetivo a cada tramo de tubería, las cuales
corresponden a la diferencia de las alturas piezométricas o LGH ideales de sus nudos inicial y
final (estimadas en la Etapa 4).
6. Cálculo del diámetro ideal de cada tubería para las pérdidas objetivo fijadas en la Etapa 5 y
para los caudales obtenidos en la simulación hidráulica del Paso 3. Para calcular los diámetros
se debe utilizar una ecuación de resistencia como la de Darcy-Weisbach o la de Hazen-
Williams.
7. Realizar una simulación hidráulica para estimar las pérdidas reales de energía que tienen
lugar en cada tubería para los nuevos diámetros calculados en la Etapa 6.
8. Cálculo del error entre las pérdidas de energía objetivo (Etapa 5) y las reales (Etapa 7).
9. Si el error entre las pérdidas de energía reales y objetivo calculado en la Etapa 8 es menor que
el error admisible o si el número de iteraciones realizadas es superior al número máximo de
iteraciones fijado al comienzo del proceso de diseño, se continúa con la Etapa 10; de lo
contrario, se debe regresar a la Etapa 3.
10. Realizar una simulación hidráulica para la configuración de diámetros que se tiene al final de
la Etapa 9; con esta simulación se determinan los caudales en las tuberías y las presiones en
todos los nudos de la red.
11. Si en al menos un nudo de la red la presión es inferior a la presión mínima, se debe realizar la
corrección de las prominencias o nudos muy elevados; de lo contrario se continúa con la
Etapa 12.
12. Aproximación de todos los diámetros al siguiente diámetro comercial (los diámetros
obtenidos al final de la Etapa 11 son continuos y deben redondearse a diámetros comerciales)
13. Aplicación de programación por restricciones para aumentar diámetros hasta que se satisfaga
el requisito de mínima presión en todos los nudos.
14. Aplicación de programación por restricciones para disminuir los diámetros de algunas
tuberías sin violar el requisito de mínima presión en todos los nudos.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
25
2.5.6. Metodología de Optimal Power Use Surface (OPUS)
La extensión de concepto básico de Wu fue propuesta por Ronald Featherstone en 1983; como
anteriormente se explicó, el sugirió su aplicación a redes que son sistemas más complejos que las
estudiadas por Wu. Este concepto ha sido utilizado en los modelos basados en la demanda con
topologías abiertas y cerradas, y más recientemente en los sistemas abiertos con demandas
impulsados por presión. El óptimo uso de energía de superficie (por sus siglas en inglés, OPUS)
metodología introducida por Takahashi et al (2010), propone un enfoque de hidráulica neta que
sigue a los criterios mencionados anteriormente, lo que demuestra que los criterios hidráulicos
podrían ser utilizados como la base de diseño de RDAP con el fin de reemplazar el enfoque
estocástico - iteración intensiva requerida por las metaheurísticas. Además, la aplicación de estos
principios hidráulicos junto con formulaciones de programación lineal (programación lineal entera
o ILP) se ha utilizado en otros estudios que se presentan en Saldarriaga et al (2012). Los resultados
obtenidos utilizando estas metodologías son excepcionales, no sólo en términos de la función
objetivo, lo que demuestra para alcanzar soluciones casi óptimas con pequeñas diferencias en
comparación con los registros mundiales, sino también en términos del esfuerzo computacional
requerido, que siempre es varios órdenes de magnitud menor que la mayoría de las soluciones
comparables alcanzados a través de diferentes enfoques. Además, este enfoque ofrece una visión
más clara de la mecánica interna que rigen el diseño de RDAP, lo que hace que sea fácil de
entender y muy versátil para ser implementado, permitiendo su acoplamiento con herramientas
tales como ILP con el fin de acelerar el proceso.
Metodología OPUS
La metodología de diseño OPUS está compuesta por seis pasos diferentes. Estos se presentan en la
Figura 1 en el orden en que deben ser ejecutadas. Cada uno de los procesos se describe a
continuación, y el algoritmo detallado que cada uno de ellos sigue se explica en el trabajo
desarrollado por Saldarriaga et al. (2012).
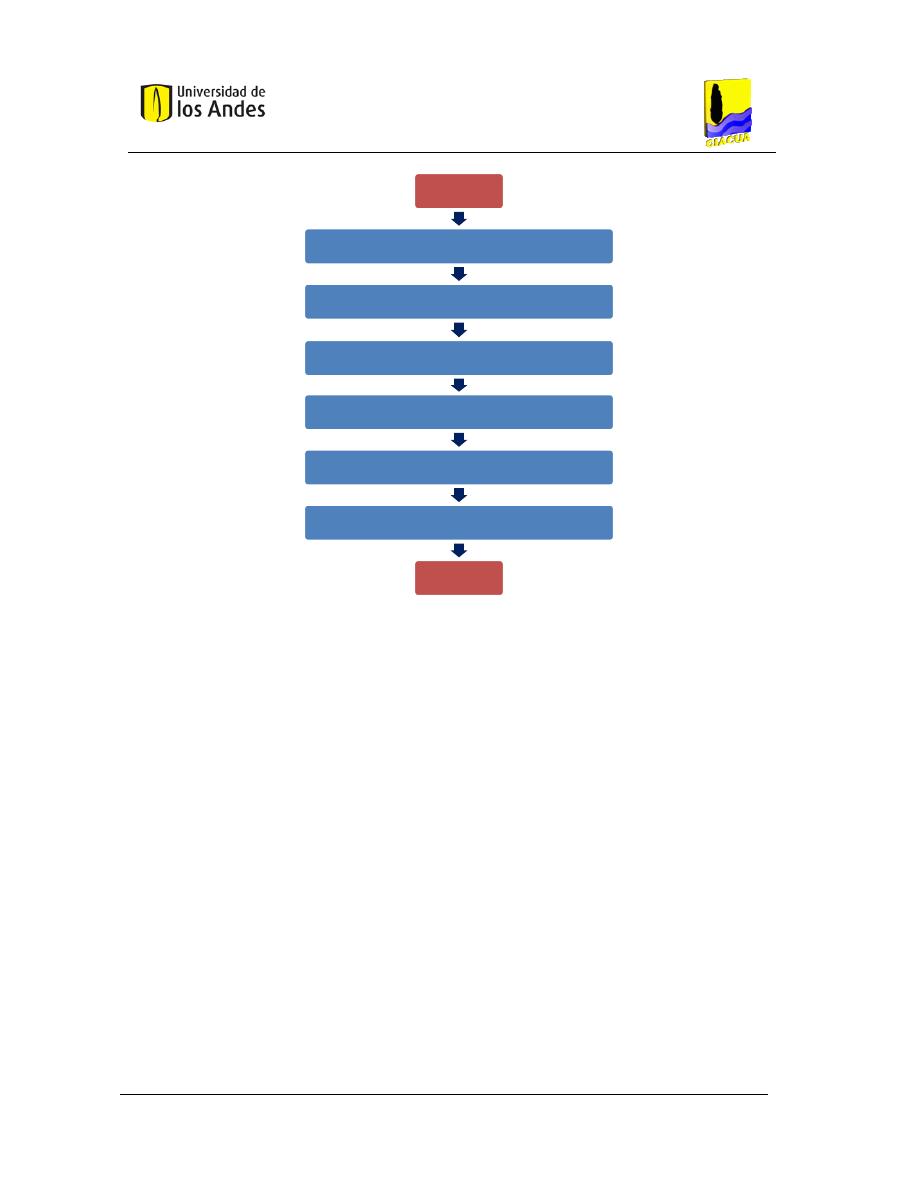
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
26
Figura 3 Diagrama BPMN de la metodología OPUS. Saldarriaga (2013).
1. Búsqueda de sumidero o árbol de la estructura
Este paso se basa en dos principios: el primero es que la RDAP de menor costo se debe abastecer
de agua a cada nudo de la demanda mediante una única ruta de las fuentes de agua. El segundo
establece que a medida que aumenta el caudal de diseño de una tubería, su costo marginal
disminuye. El primer principio viene del hecho de que la redundancia, aunque favoreciendo la
fiabilidad, es hidráulicamente ineficiente y por lo tanto las RDAP abiertas son mucho más baratas
que las redes con circuitos. El segundo principio se deriva de la expresión del flujo derivado de las
ecuaciones de Darcy-Weisbach y Colebrook-White. Dejando todos los otros parámetros
constantes, el flujo (Q) presenta una relación aproximadamente proporcional con el diámetro a
una potencia de 2,6. Suponiendo una ecuación costo tubería estándar y reemplazando el diámetro
de acuerdo con esta proporción, el costo por unidad de longitud de un tubo como una función de
su flujo de diseño se comporta como se muestra en la Figura 4.
Inicio
Búsqueda sumidero o árbol de la estructura
Optimal power use surface
Distribución del flujo óptimo
Calculo del diámetro
Redondeo de diámetro
Optimización
Fin
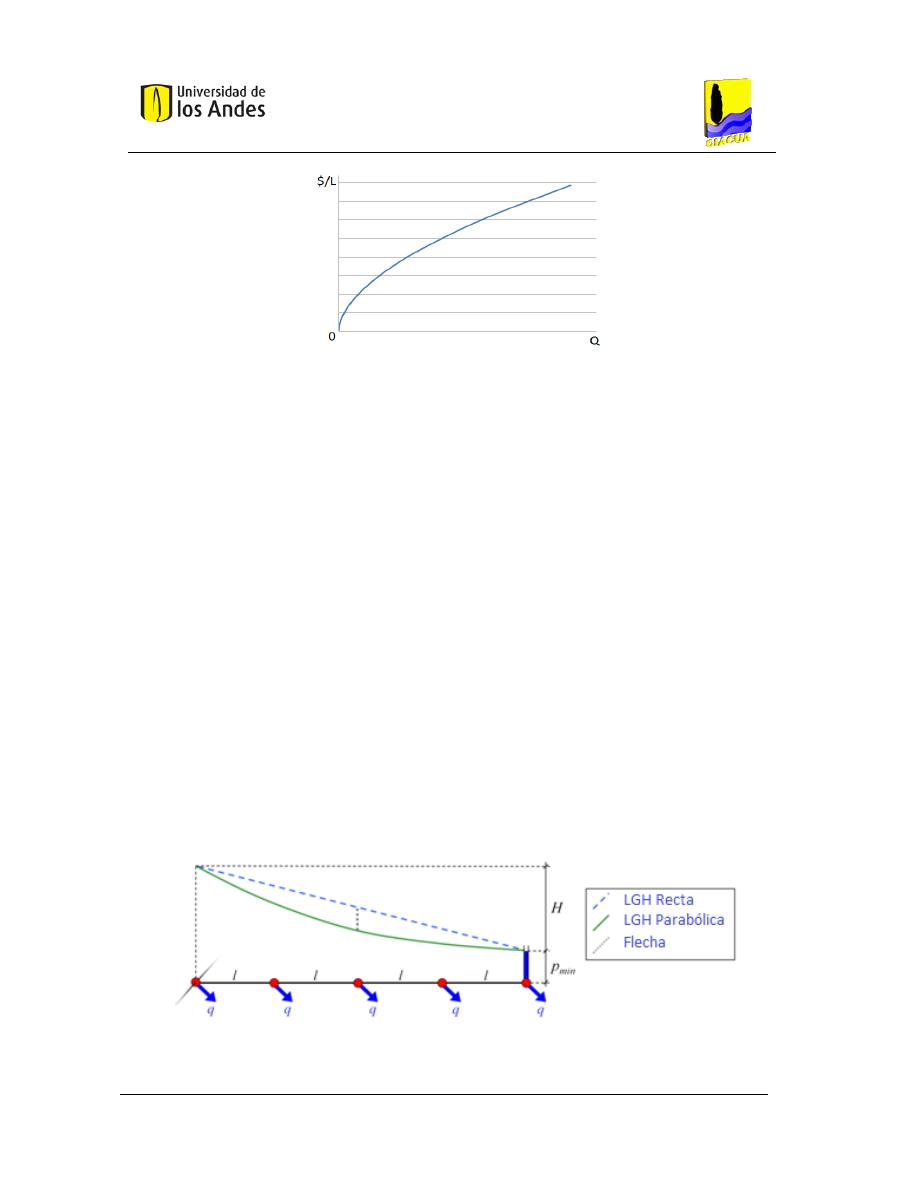
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
27
Figura 4 Relación esquemática entre el costo de tubería y caudal. Saldarriaga (2013).
Por lo tanto, el objetivo de este sub - proceso es descomponer la red con circuitos en una
estructura abierta (es decir, el agua sólo puede ser transportado a través de un camino desde el
depósito a cualquier nudo en el sistema) con el fin de identificar los nudos de sumidero, que son
nudos con una altura piezométrica más bajo que todos sus vecinos y por lo tanto en una red
abierta son nudos sin nudos descendentes. Una función de costo -beneficio se utiliza para montar
la red abierta, y una vez hecho esto, el paso óptimo de la utilización a la superficie se puede iniciar.
2. Optimal Power Use Surface (OPUS)
Esta etapa consiste en la asignación de una altura piezométrica objetivo de todos los nudos de la
red y por lo tanto predefinir las pérdidas de altura de cada tubo. Este sub- proceso le da el nombre
a toda la metodología, ya que es aquí donde se aplica el concepto I- Pai Wu de línea de gradiente
hidráulico óptima. Mediante la asignación de todos los nudos sumidero de la presión mínima
permitida, y conociendo la altura en el embalse, la altura de los nudos intermedios " para cada
ruta se calcula con un LGH parabólico como se muestra en la Figura 5. El valor óptimo de la flecha
puede estimarse utilizando una metodología propuesta por Ochoa et al (2009), quienes
encontraron que depende de la distribución de la demanda, el cociente entre las demandas de
flujo y longitud de la tubería, y la función de costo. Como resultado de la sub - proceso cada nudo
en la red se ha asignado una altura piezométrica objetivo y por lo tanto se necesita un flujo de
diseño con el fin de calcular el diámetro de cada tubo en la red.
Figura 5 El criterio de la I- Pai Wu para predefinir la altura en cada nudo. Saldarriaga (2013).

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
28
3. Distribución óptima del caudal
Teniendo en cuenta que en una red con circuitos una misma superficie de gradiente hidráulico
puede obtenerse a través de muchas configuraciones diferentes de diámetro cuando el conjunto
de tubos de tamaños permisibles es
(números reales positivos), es necesario predefinir
también el flujo objetivo para cada tubería con el fin de obtener una configuración de diámetro
que minimiza los costos. Por lo tanto, este subproceso pretende encontrar un esquema único de
distribución de flujo que respete la conservación de la masa y se ajusta a la Optimal Power Use
Surface previamente establecida. Para llevar a cabo esta tarea de manera que el resultado final
minimice los costos, los principios utilizados en la primera etapa se utilizan una vez más y, como
resultado, la metodología decide para cada nudo que tubo de aguas arriba (en la red con circuitos)
es el principal, es decir, la tubería que se transportaba la parte más alta de flujo. Esto implica que
el resto de los tubos deben transmitir el flujo que se corresponde con el diámetro mínimo. Para
determinar la tubería principal, se evalúa la función
⁄ para cada tubo y el que tiene el valor
máximo es el seleccionado. Al final de este paso, todas las tuberías en el sistema deben haber
asignado un caudal de diseño.
4. Cálculo del diámetro
Este subproceso calcula diámetros continuos para cada tubo con el resultado de los pasos
anteriores. Como ya se conocen las pérdidas de altura objetivas y la tasa de flujo de diseño para
cada tubo, el diámetro continuo necesario puede obtenerse fácilmente a partir de un cálculo
directo. Este cálculo es explícito cuando se utiliza la ecuación de Hazen-Williams e iterativo cuando
se emplean las ecuaciones de Darcy-Weisbach y Colebrook-White. El diseño continuo resultante
es, en teoría, una RDAP- completa operativa, con un costo muy cerca del mínimo. Debido a la
limitada disponibilidad de tamaños de diámetro, se requiere un siguiente paso para transformar
este diseño "óptimo " a un diseño que pueda ser construido en la realidad con los diámetros
comerciales disponibles.
5. Redondeo de diámetros
Esta etapa consiste en la aproximación de cada diámetro continuo a un valor discreto de la lista de
tamaños de diámetro disponibles comercialmente. Saldarriaga et al (2012) encontraron que el
redondeo al valor de flujo equivalente más cercano ofrece los mejores resultados. Se encontró
que la mejor manera de lograr que se aproxime al flujo más cercano, es mediante la elevación de
los valores de diámetro a una potencia de 2,6 y el posterior redondeo de estos valores.
Desafortunadamente, este paso afecta drásticamente el comportamiento hidráulico del sistema,
sobre todo si todos los tamaños de diámetro se redondean hacia arriba o hacia abajo.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
29
6. Optimización
Este último paso tiene dos objetivos principales: el primero es asegurarse de que cada nudo tiene
una presión mayor o igual que el mínimo permitido. La segunda es la búsqueda de posibles
reducciones de costos. El primer objetivo se alcanza mediante el aumento de diámetro (si es
necesario), comenzando con los que tienen diferencia de altura de pérdida de unidad mayor entre
los valores reales y objetivos, hasta que todo el sistema cumple con la restricción de presión. El
segundo objetivo se alcanza a través de un doble barrido a partir de los embalses que van hacia los
sumideros en la dirección del flujo, y luego hacia atrás. La reducción del diámetro de cada tubo se
considera dos veces, y el diámetro se reduce de forma permanente sino se viola ninguna
restricción después del cambio. Para asegurarse de que la presión mínima no está siendo violada
se requieren numerosas simulaciones hidráulicas, ya que es necesario ejecutar una simulación
hidráulica por la modificación diámetro de cada tubo individual. Este único proceso podría ser
utilizado solo para obtener diseños funcionales, a pesar de esto, es fuertemente dependiente de la
configuración inicial de diámetro.
A partir de probar la metodología en tres sistemas de referencia conocidos: Hanoi, Balerma y
Taichung, así como en la red R28 que también se introduce en este trabajo, Saldarriaga et al
(2012) concluyeron que la metodología OPUS es determinista y por lo tanto un diseño idéntico
sería encontrado por cualquier usuario después de que el mismo número de iteraciones,
contrariamente a otros algoritmos que poseen un componente estocástico. Esta metodología es
mucho más eficiente que las técnicas heurísticas y los esfuerzos realizados para comprender los
principios hidráulicos están bien recompensados. La solución obtenida a través de OPUS ofrece
una muy buena configuración inicial a los algoritmos no deterministas, reducir el número de
iteraciones necesarias para llegar a resultados casi óptimas a través de metaheurísticas y
proporcionar una búsqueda más amplia del espacio de soluciones. Este es el motivo por el que es
adecuado para ser utilizado como un Hot Start para metaheurísticas, con el objetivo de mejorar
los resultados alcanzados a través de la aplicación de los principios hidráulicos. Esta última idea, es
la motivación del presente trabajo.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
30
2.6. Programas
2.6.6. Programa REDES
El programa REDES, desarrollado en el Centro de
Investigaciones en Acueductos y Alcantarillados CIACUA
de la Universidad de Los Andes, Bogotá, Colombia, es
una herramienta de simulación de sistemas de tuberías
con flujo a presión.
El desarrollo del programa REDES está basado en
criterios de optimización de Redes de Distribución de
Agua Potable (RDAP) a los que se ha llegado a través de
investigaciones en diferentes universidades de Estados
Unidos y Europa. Entre los criterios más importantes se
encuentran los de optimización económica de diámetros
de tuberías en redes cerradas de distribución de agua,
desarrollados por Ronald Featherstone y Karim El-Jumaily (basados en el criterio de Wu), el
Método del Fradiente para el cálculo de redes cerradas de distribución de agua, desarrollado por
Ezio Todini y Enda O´Connell y el método de Superficie Óptima de Gradiente Hidráulico,
desarrollado por Susana Ochoa como tesis de magíster.
A diferencia de otros programas comerciales, el programa REDES permite el diseño optimizado de
RDAP, tanto de redes nuevas como de ampliaciones de redes existentes. En su módulo de diseño
incluye las opciones para diseñar con diferentes métodos: Algoritmos Genéticos aplicados al
diseño de redes, Superficie Óptima de Presiones (SOP), Programación por Restricciones y
Superficie Óptima de Gradiente Hidráulico (SOGH).
2.6.6.1.
Características del Programa
La interfaz gráfica de REDES consiste en un mapa de la red en la cual es posible visualizar los
valores de diferentes variables de los elementos; de igual forma se pueden apreciar a través de
curvas de nivel y de superficies, de manera que el usuario pueda tener una idea global de lo que
ocurre en la red.
2.6.6.2.
Características del Programa
Hasta la red más simple está compuesta por al menos una fuente de agua, un tubo y un nudo de
demanda; sin embargo, redes más complejas pueden tener diferentes accesorios, como emisores,
válvulas o bombas hidráulicas. El programa REDES maneja siete tipos de elementos diferentes,
presentados a continuación:
Embalses: son fuentes de agua cuya altura piezométrica es fija.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
31
Tanques: fuente de agua cuya altura piezométrica es variable, ya que pueden tener un
caudal de entrada y alimentar la red o pueden ser alimentados por la red y tener un
caudal de salida.
Nudos: puntos donde hay demanda de caudal.
Tuberías: tuberías de la red.
Emisores: elementos hidráulicos de los nudos que permiten simular fugas y emisores en
sistemas de riego.
Válvulas: accesorios de las tuberías que combinan la relación entre altura piezométrica y
el caudal; se pueden modelar válvulas reductoras de presión, válvulas reguladoras de
presión, válvulas de control de caudal, válvulas de propósito general, válvulas de
regulación de cierre y válvulas de cheque.
Bombas: accesorios de las tuberías que proporcionan energía a la red.
2.6.6.3.
Capacidades del Programa.
El programa REDES ofrece múltiples opciones de cálculo al usuario; entre estas se encuentra el
cálculo hidráulico estático (cálculo de alturas piezométricas y presiones), cálculo hidráulico en
periodo extendido (cálculo hidráulico a diferentes horas del día), cálculo de la calidad de agua
(concentraciones, edad, trazadores y porcentaje de procedencia), diseño de RDAP con métodos
modernos, calibración de redes y cálculo del Índice de Resiliencia.
2.6.7. Programa EPANET
EPANET es un programa desarrollado por la Agencia de Protección Ambiental de Estados Unidos
(EPA, Enviromental Protection Agency), para el estudio y análisis del comportamiento de redes
hidráulicas a presión. El programa está compuesto por un módulo de análisis hidráulico que
permite simular el comportamiento dinámico de una RDAP. Hace posible incorporar a la
simulación tuberías, bombas de velocidad fijas y velocidad variable, válvulas de estrangulación,
válvulas reductoras y sostenedoras de presión, tanques de altura piezométrica constante o
variable y sistemas de control y operación temporales o según nivel y presión.
El programa se encuentra escrito en lenguaje C y puede correr en entornos MS-DOS o UNIX o
Windows, siendo este último sistema operacional el más popular debido a su facilidad de manejo y
la excelente presentación de los resultados por pantalla. El programa es bastante rápido y
confiable; el tamaño de la red solo puede verse limitado por las capacidades de memoria del
equipo utilizado. La entrada de datos se hace a través de un archivo input de tipo texto con toda la
información de entrada. Adicionalmente, los resultados obtenidos por el programa son bastante
confiables; la popularidad del EPANET se ha extendido rápidamente por su buen desempeño y por
ser de distribución gratuita. Las ventajas expuestas, motivaron a los desarrolladores de software
del Centro de Investigaciones en Acueductos y Alcantarillados CIACUA de la Universidad de Los
Andes a incorporar el motor hidráulico de EPANET al programa REDES con el fin agilizar el tiempo
de cálculo de la metodología contenida en el programa, OPUS.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
32
2.7. Metodología de redondeo, aumento y disminución de diámetros
(RAD) desarrollada para OPUS en el programa REDES
2.7.6. Metodología de redondeo de diámetros y posterior optimización
La metodología OPUS corresponde a la expansión a la metodología desarrollada para el diseño de
series de tuberías, la cual se basa determinar la forma de la LGH óptima de un sistema de
distribución y a partir de ésta calcular los diámetros de las tuberías que generan tal LGH y que
conforman un diseño cercano al de mínimo costo. La metodología OPUS es similar a la
metodología SOP, pero tiene dos rasgos nuevos y diferentes:
1. Redondeo de diámetro: Esta etapa consiste en la aproximación de cada diámetro
continuo a un valor discreto de la lista de tamaños de diámetro disponibles
comercialmente. Saldarriaga et al (2012) encontró que el redondeo al valor de flujo
equivalente más cercano ofrece los mejores resultados. Se encontró que la mejor
manera de lograr que se aproxime al flujo más cercano, es mediante la elevación de los
valores de diámetro a una potencia de 2,6 y el posterior redondeo de estos valores.
Desafortunadamente, este paso afecta drásticamente el comportamiento hidráulico del
sistema, sobre todo si todos los tamaños de diámetro se redondean hacia arriba o hacia
abajo.
2. Optimización: Este último paso tiene dos objetivos principales: el primero es asegurarse
de que cada nudo tiene una presión mayor o igual que el mínimo permitido. La segunda
es la búsqueda de posibles reducciones de costos. El primer objetivo se alcanza
mediante el aumento de diámetro (si es necesario), comenzando con los que tienen
diferencia de altura de pérdida de unidad mayor entre los valores reales y objetivos,
hasta que todo el sistema cumple con la restricción de presión. El segundo objetivo se
alcanza a través de un doble barrido a partir de los embalses que van hacia los
sumideros en la dirección del flujo, y luego hacia atrás. La reducción del diámetro de
cada tubo se considera dos veces, y el diámetro se reduce de forma permanente si se
viola ninguna restricción después del cambio. Para asegurarse de que la presión mínima
no está siendo violada se requieren numerosas simulaciones hidráulicas, ya que es
necesario ejecutar una simulación hidráulica por la modificación diámetro de cada tubo
individual. Este único proceso podría ser utilizado solo para obtener diseños
funcionales
5
, a pesar de esto, es fuertemente dependiente de la configuración inicial de
diámetro.
5
Un diseño funcional se refiere a un diseño que pueda ser construido en la realidad con los diámetros
comerciales disponibles.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
33
Etapas que conforman la metodología:
Cada una de las etapas que se enuncia a continuación corresponde a un proceso complejo
compuesto por múltiples actividades; es por eso que a éstas se les denomina “etapas” y a las
actividades que las conforman se les denomina “pasos”. Las etapas son el redondeo de diámetro y
la optimización, que básicamente redondean a diámetros comerciales los diámetros continuos,
aumentan dichos diámetros comerciales para cumplir presiones mínimas y finalmente reducen los
diámetros para avatar los costos de construcción. Dado que el implica el redondeo, el aumento y
la disminución del diámetro, el autor se refiere a este como la metodología RAD (Redondeo,
Aumento y Disminución).
Etapa de redondeo de diámetros
El algoritmo de redondeo desarrollado es bastante simple: éste consiste en aproximar el diámetro
continuo calculado para cada tubo al diámetro comercial disponible de acuerdo a 3 reglas de
decisión:
Aproximar al siguiente
Aproximar al anterior
Redondeo potencial (con la potencia deseada)
2.7.7. Redondeo aproximando al siguiente/anterior diámetro comercial
Los pasos del algoritmo de redondeo para los casos de aproximar al anterior y aproximar al
siguiente se describen a continuación:
1) Inicializar el proceso en i = 1, donde i corresponde a la posición de cada tubo dentro
de la serie.
2) Leer el diámetro del tubo i.
3) Leer el siguiente/anterior diámetro comercial disponible al diámetro del tubo i.
4) Cambiar el diámetro del tubo i del paso 2 por el diámetro del tubo i leído en el paso
3.
5) i = i + 1 (se pasa al siguiente tubo de la serie).
6) Si i es menor que NT (NT = número de tubos que conforman la serie), regresar al
Paso 2, de lo contrario, finalizar el algoritmo.
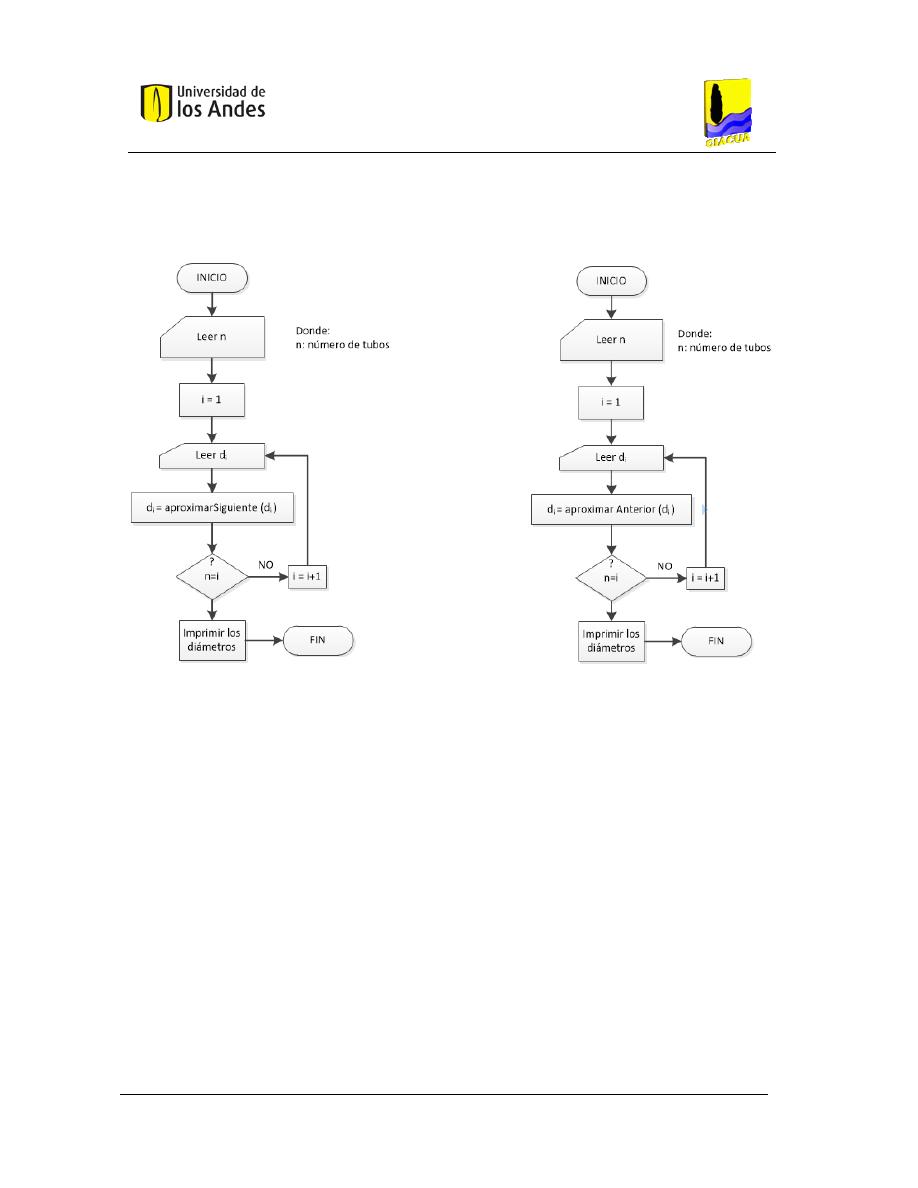
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
34
Los siguientes esquemas permiten visualizar el procedimiento que se acaba de describir.
2.7.8. Redondeo aproximando a la Potencia
Los pasos del algoritmo de redondeo potencial se describen a continuación:
1) Inicializar el proceso en i = 1, donde i corresponde a la posición de cada tubo dentro
de la serie.
2) Leer el diámetro del tubo i.
3) Leer el siguiente y el anterior diámetro comercial disponible al diámetro del tubo i.
4) Calcular las siguientes dos diferencias: |
| y
|
|. El valor de la potencia es elegido por el usuario.
Diagrama de flujo 1. Redondeo aproximando
al siguiente diámetro comercial. Por el autor.
Diagrama de flujo 2. Redondeo aproximando
al anterior diámetro comercial. Por el autor.
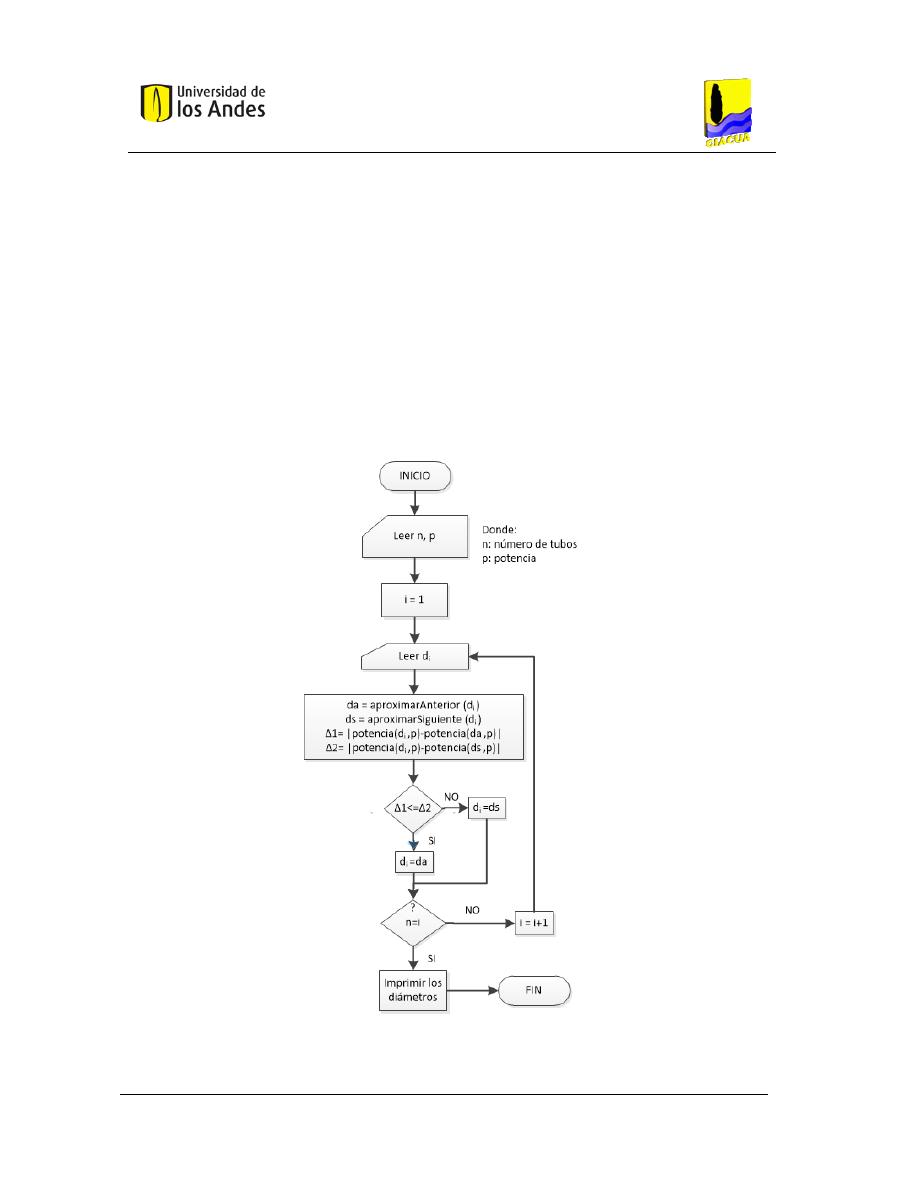
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
35
5) Elegir el nuevo diámetro del tubo i según la siguiente regla de decisión: Si
|
| |
| se toma el
diámetro anterior, de lo contrario se toma el diámetro siguiente.
6) Cambiar el diámetro del tubo i del paso 2 por el diámetro del tubo i leído en el paso
5.
7) i = i + 1 (se pasa al siguiente tubo de la serie).
8) Si i es menor que NT (NT = número de tubos que conforman la serie), regresar al
Paso 2, de lo contrario, finalizar el algoritmo.
El siguiente esquema permite visualizar el procedimiento que se acaba de describir.
Diagrama de flujo 3. Redondeo aproximando a la potencia. Por el autor

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
36
Etapa de optimización
Esta etapa comprende dos grandes procedimientos; el primero garantiza que no haya déficit de
presión y el segundo plantea una optimización del costo constructivo de la red que cumpla con la
restricción de presión.
Aumento de diámetros: para evitar déficit de presión
El primer procedimiento se conoce como Aumento de Diámetros: para evitar déficit de presión, su
importancia parte del hecho que en la anterior etapa al pasar de diámetros continuos a discretos
(comerciales) las condiciones hidráulicas pueden verse afectadas negativamente, generando
presiones mínimas menores a la permitida. Este procedimiento elige un tubo de acuerdo con un
criterio de decisión elegido por el usuario, el cual es aumentando. Los criterios de decisión
disponibles en REDES 2013 son:
Sf: Tubo con mayor relación |H/L|
Htotales: Tubo con mayor |H|
Puti: Tubo con mayor producto H*Q
(H/L)*(Q(Qt): Tubo con mayor relación |H/L|*Q/Q
Delta H_L: Tubo con mayor relación |(Hreal-Hideal)/L|
Delta H: Tubo con mayor relación |(Hreal-Hideal)/L|
Q x H: Tubo con mayor producto |H*Q|

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
37
El procedimiento de elegir un tubo para ser aumentado se repite las veces que sea necesario hasta
cumplir con la presión mínima.
2.7.9. Algoritmo de aumentar diámetros
Los pasos del algoritmo de Aumentar de Diámetros para evitar déficit de presión (con el criterio de
decisión Sf a manera de ejemplo), se describen a continuación:
1) Leer la presión mínima (M.C.A) ingresada como parámetro por el usuario.
2) Calcular la hidráulica (con el calculador hidráulico deseado por el usuario:
SparseSolver o Epanet) de la red actual y leer la presión mínima de dicha red.
3) Si la presión mínima de la red actual es menor que la presión mínima ingresada
como parámetro ir a las paso 4, de lo contrario ir a las 13.
4) Inicializar el proceso en i = 1, donde i corresponde a la posición de cada tubo
dentro de la serie. Inicializar la variable con un valor de 0 (cero).
5) Leer el diámetro, la longitud y las pérdidas totales del tubo i. Leer el diámetro
comercial máximo disponible.
6) Calcular la siguiente relación:
7) Leer el diámetro comercial máximo disponible.
8) Si
la
relación
y
el
, se elige el tubo i. En caso de que
ningún tubo cumpla con ambos criterios ir al paso 14.
9) i = i + 1 (se pasa al siguiente tubo de la serie).
10) Si i es menor que NT (NT = número de tubos que conforman la serie), regresar
al Paso 5, de lo contrario, imprimir el ultimo tubo seleccionado en el paso 8 y
continuar al paso 11.
11) Aproximar al siguiente diámetro el tubo seleccionado.
12) Regresar al paso 2.
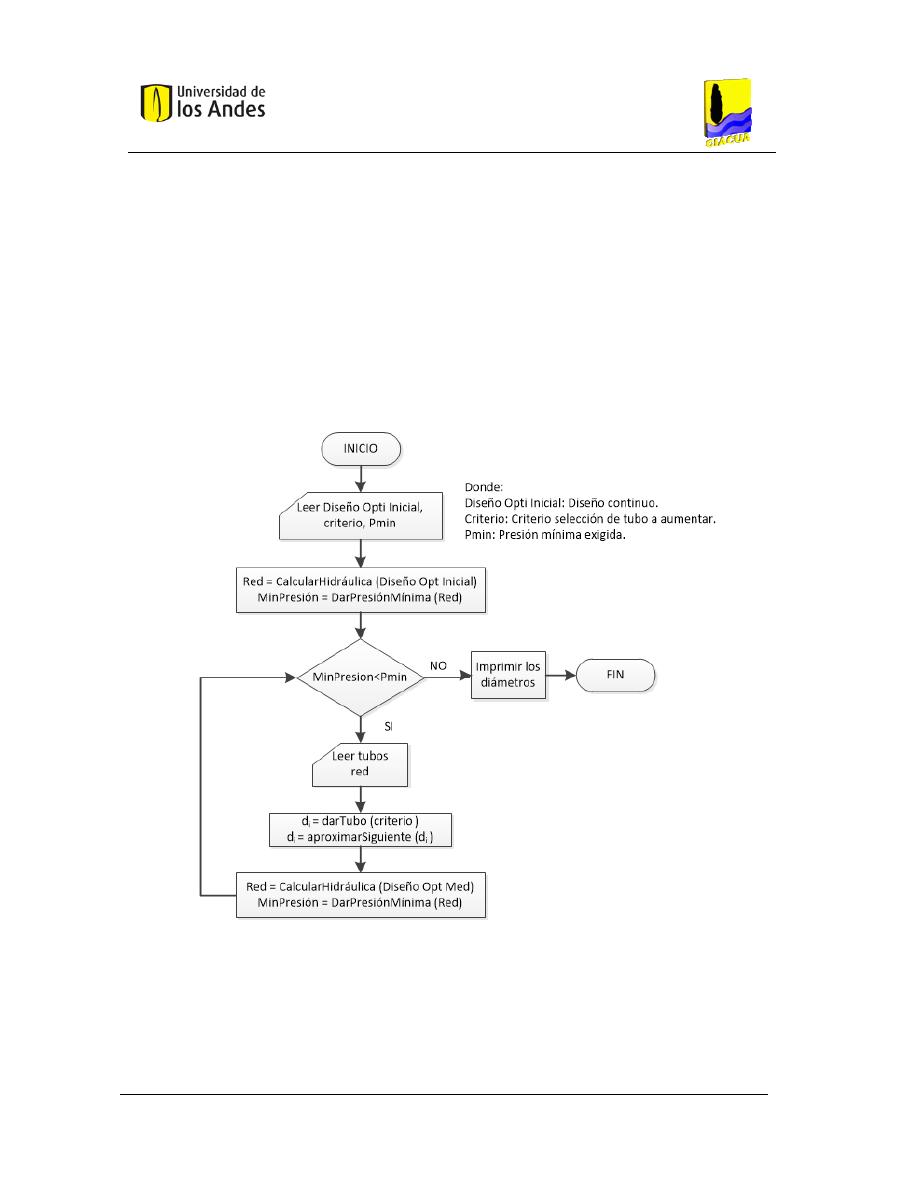
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
38
13) Finalizar el algoritmo.
14) Informar que: El diámetro máximo en todas las tuberías no puede garantizar la
presión mínima. Hay 3 posibles razones: (1) El diámetro máximo es muy
pequeño, (2) La LGH de los embalses es insuficiente y (3) La presión mínima
ingresada como parámetro es muy grande. Ir al paso 13.
Para el caso de los otros 6 criterios solo se deben cambiar los pasos 5 al paso 8.
El siguiente esquema permite visualizar el procedimiento que se acaba de describir.
Diagrama de flujo 4. Aumentar Diámetros para evitar déficit de presión. Por el autor.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
39
Disminuir diámetros: para reducir costos constructivos
El segundo procedimiento se conoce como Disminuir Diámetros: para reducir costos constructivos,
su importancia parte de hecho que en el anterior proceso de asegurar la presión mínima en todos
los nudos aumentando el tamaño de las tuberías puede generar sobre costos. Este procedimiento
ordena las tuberías de acuerdo con un criterio de ordenamiento, para posteriormente recorrer
dicha lista e ir disminuyendo tubo a tubo desde que dicha reducción cumpla con la presión
mínima. Los criterios de ordenamiento probados anteriormente para este algoritmo son:
Diámetro.
Longitud.
Rugosidad.
Coeficiente pérdidas menores.
Caudal.
Velocidad.
Número de Reynolds.
Pérdidas totales.
Pérdidas por fricción.
Pérdidas menores.
Factor de fricción.
Tiempo de retención.
Volumen
Delta H_L: Hreal-Hideal
Distancia mínima.
Pérdidas por unidad de longitud.
Consecutivo.
Las listas se ordenan de acuerdo con los anteriores criterios de menor a mayor. Para el algoritmo
de Disminuir Diámetros se determinó que el mejor criterio de ordenamiento es el de distancia
mínima promedio al embalse; por lo tanto en el código interno de REDES 2013 este parámetro de
ordenamiento es estático.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
40
2.7.10. Algoritmo de Disminuir Diámetros
Los pasos del algoritmo de disminución de diámetros para reducir costos de construcción, se
describen a continuación:
1) Leer la presión mínima (M.C.A) ingresada como parámetro por el usuario y leer
el diámetro comercial mínimo disponible.
2) Ordenar las tuberías de la red en una lista de manera ASCEDENTE de acuerdo
con la distancia mínima promedio al embalse.
3) Inicializar el proceso en i = 1, donde i corresponde a la posición de cada tubo
dentro de la serie.
4) Leer el diámetro del tubo i y leer el anterior diámetro comercial disponible al
diámetro del tubo i.
5) Si
cambiar el diámetro del tubo i del
paso 4 por el diámetro del tubo i leído en el paso 5.
6) Calcular la hidráulica (con el calculador hidráulico deseado por el usuario:
SparseSolver o Epanet) de la red actual y leer la presión mínima de dicha red.
7) Si la presión mínima de la red actual es menor que la presión mínima ingresada
como parámetro regresar el diámetro del tubo i a diámetro leído en el paso 4.
8) i = i + 1 (se pasa al siguiente tubo de la serie).
9) Si i es menor que NT (NT = número de tubos que conforman la serie), regresar
al Paso 4, de lo contrario, ir a la paso 11 si el criterio de ordenamiento actual es
ascendente, en caso de ser descendente ir al paso 12.
10) Ordenar las tuberías de la red en una lista de manera DESCENDENTE de acuerdo
con la distancia mínima promedio al embalse e ir al paso 3.
11) Imprimir los diámetros y finalizar el algoritmo.
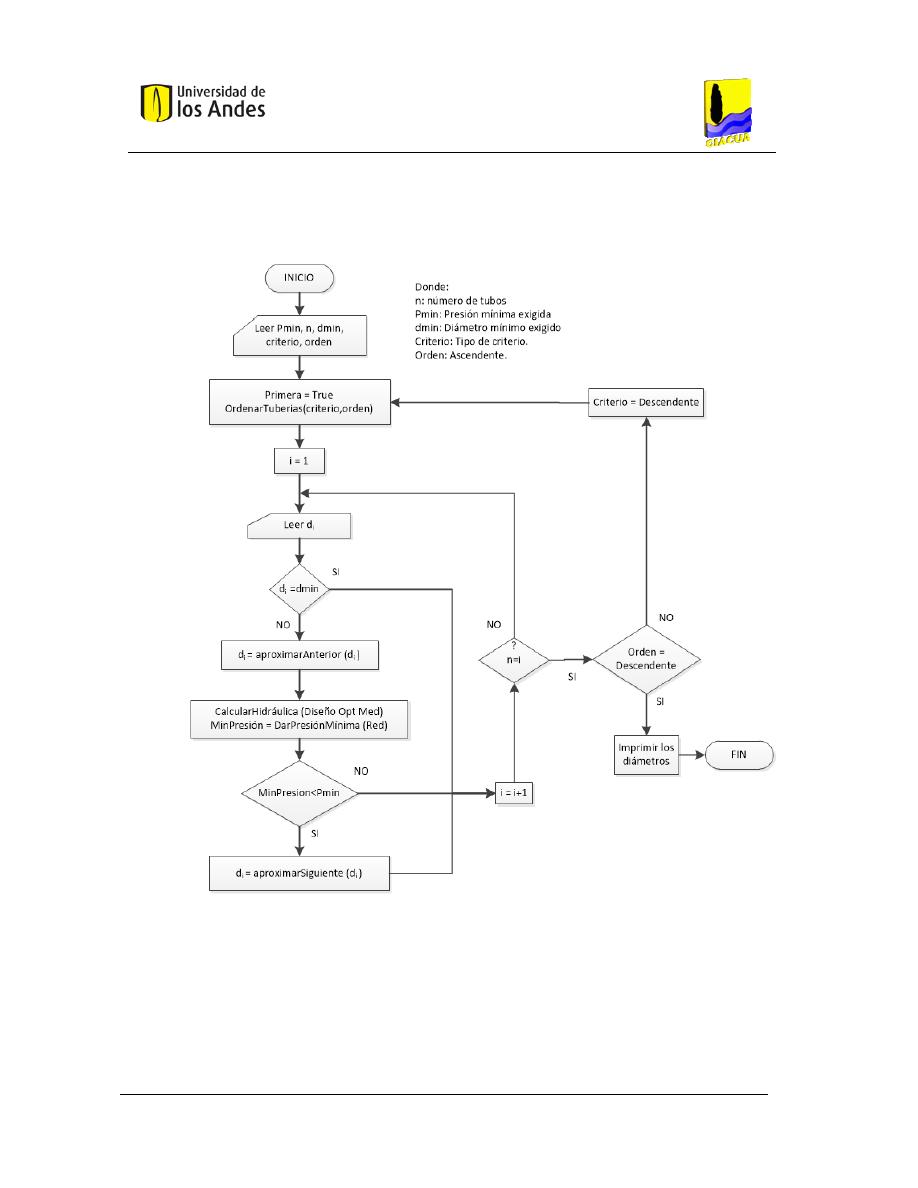
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
41
El siguiente esquema permite visualizar el procedimiento que se acaba de describir.
Diagrama de flujo 5. Disminución de diámetros para reducir costos. Por el autor.
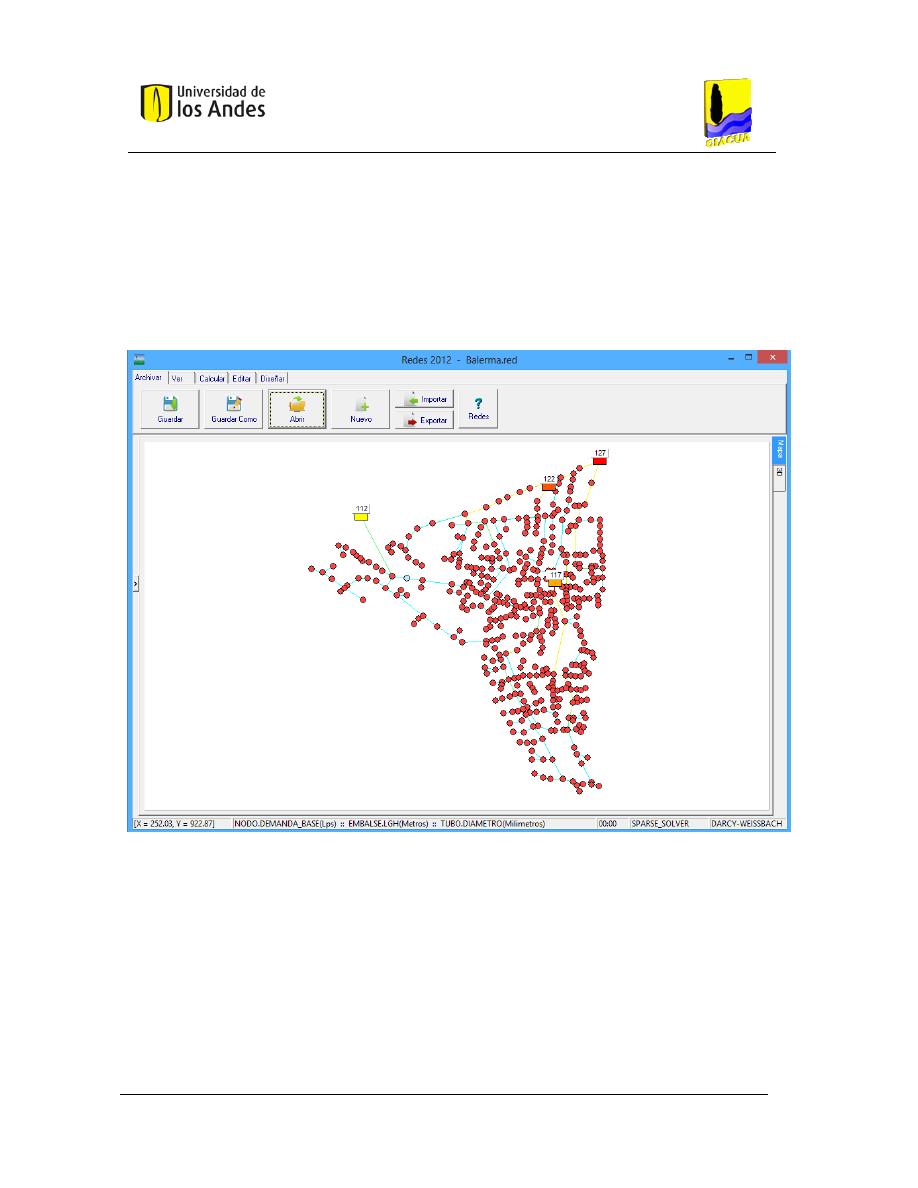
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
42
2.7.11. Uso de la metodología de redondeo, aumento y disminución de
diámetros desarrollada para OPUS en el programa REDES.
Con el fin de hacer ilustrativo el uso de la metodología de redondeo, aumento y disminución de
diámetros desarrollada para OPUS en el programa REDES, las siguientes ilustraciones muestran el
procedimiento que llega a cabo el usuario para hacer uso de la metodología en el programa REDES
2013.
Figura 6 Ventana del programa REDES 2013 con la Red Balerma.
Al abrir un archivo tipo RED, la red se visualiza en la pestaña de mapa del programa. Como se
observa en la Figura 6 en la barra informativa de la parte inferior de la ventana, por defecto se
tiene como calculador hidráulico SparseSolver y ecuación hidráulica la de Darcy-Weisbach. El
siguiente paso es ir a la pestaña Diseñar (si se desea cambiar el calculador hidráulico ir a Calcular-
Cambiar Calculador Hidráulico).
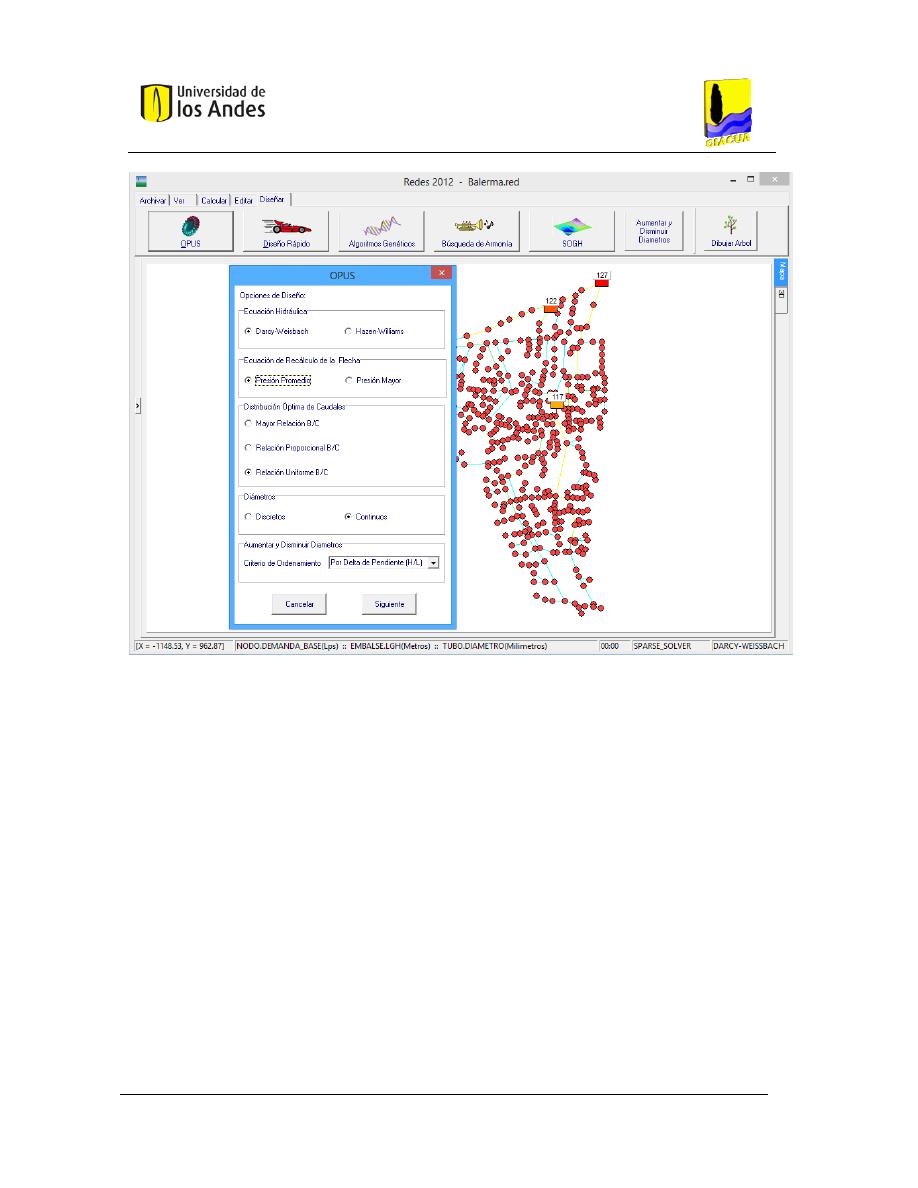
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
43
Figura 7 Ventana para ingresar las opciones de diseño del modulo OPUS.
En la pestaña Diseñar se encuentran las opciones de diseño OPUS (ver Numeral 2.5.6), algoritmos
genéticos (ver Numeral 2.5.1), búsqueda de armonía (ver Numeral 2.5.2) y SOGH (ver Numeral
2.5.7). Al elegir la opción de OPUS la ventana emergente permite cambiar la ecuación hidráulica,
cambiar la ecuación de recalculo de la flecha (el concepto de flecha fue analizado en el Numeral
2.5.6), elegir la distribución óptima de caudales y finalmente las opciones relacionadas con la
metodología en consideración. En primer lugar está la opción de elegir que los diámetros sean
discretos o continuos; en caso de elegir la primera opción la ventana emergente es la que se
muestra en la Figura 8.
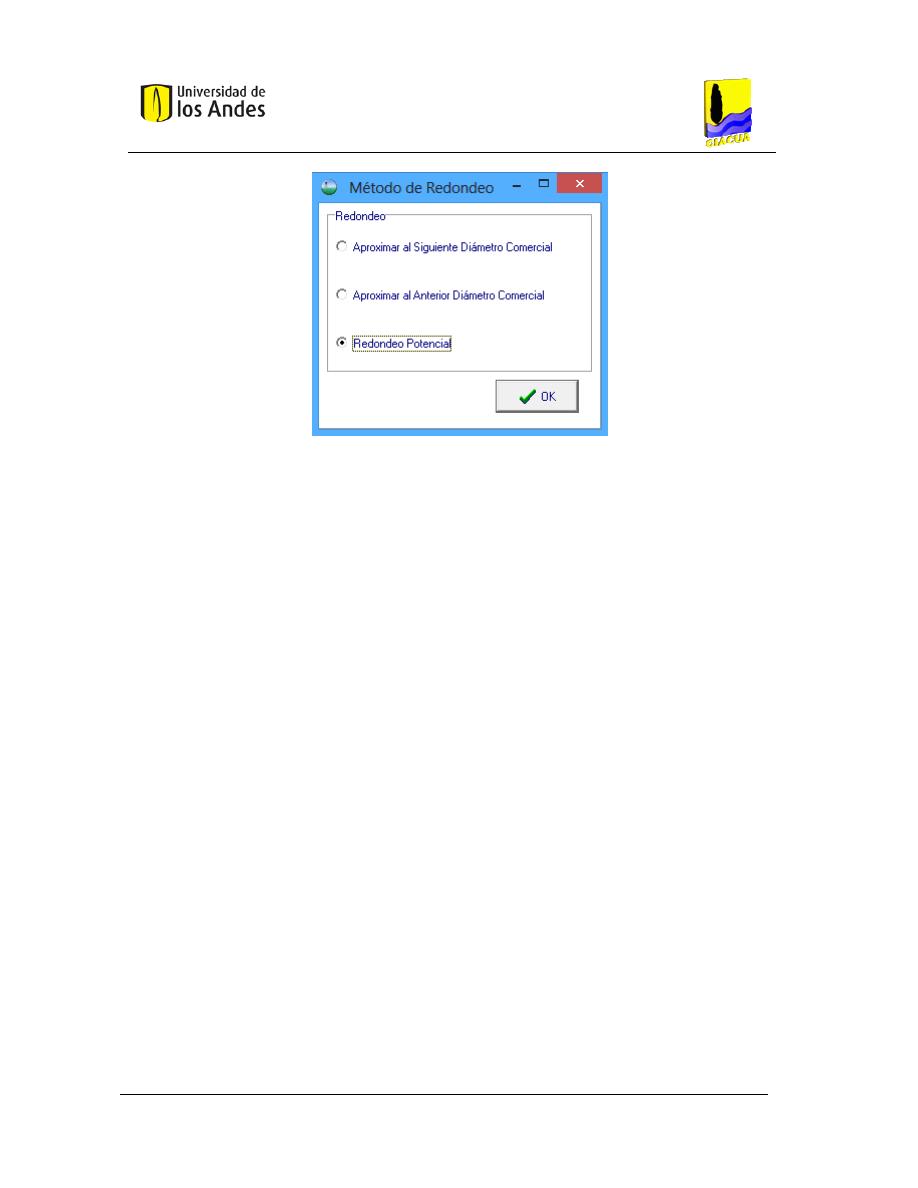
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
44
Figura 8 Ventana para elegir el tipo de redondeo deseado.
Esta ventana permite entonces elegir alguno de los procedimientos analizados en los Numerales
2.8.7 (Aproximar al siguiente o al anterior diámetro) y 2.8.8 (Redondeo Potencial), para redondear
el diseño continuo arrojado por OPUS.
Finalmente la última opción de la ventana en la ilustración figura 9 permite elegir el criterio de
selección para el algoritmo de aumentar diámetros (ver Numeral 2.8.9). Las diversas opciones se
observan en la siguiente figura.
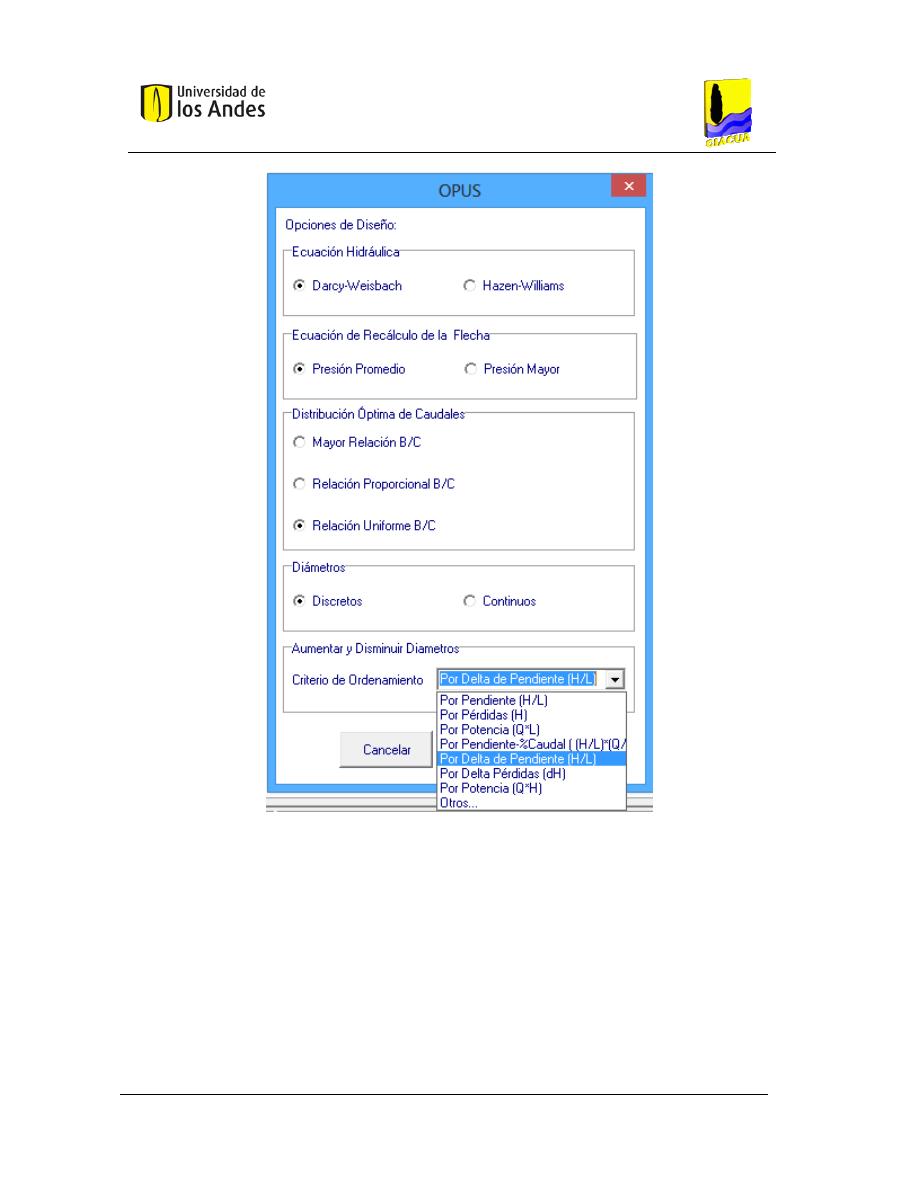
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
45
Figura 9 Ventana de opciones de diseño con lista de criterios para aumentar diámetros.
Luego de elegir alguna de las opciones de la lista que se observa en la Figura 9, el usuario debe dar
clic en el botón aceptar. A continuación se abre una nueva ventana donde se ingresan los
parámetros generales de la red a diseñar:
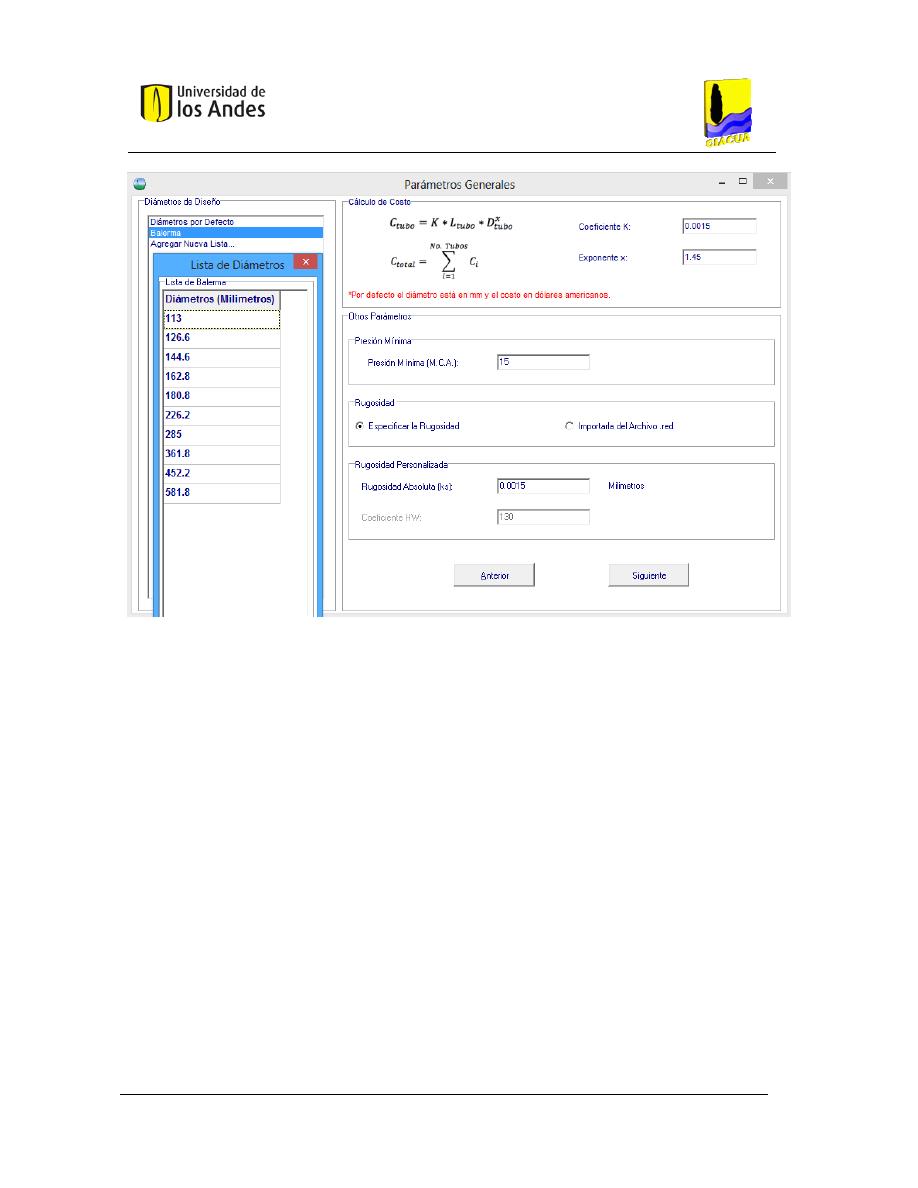
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
46
Figura 10 Ventana de para ingresar los parámetros generales de la red.
En la Figura 10 se observa que los parámetros generales de la red que desea analizar el usuario, los
parámetros que se deben ingresar son:
Lista de diámetros comerciales.
Coeficiente K y exponente x de la ecuación del cálculo de costo.
La presión mínima en metros de columna de agua.
La rugosidad absoluta o el coeficiente de Hazen-Williams.
Luego de ingresar los parámetros, al elegir el botón siguiente se despliega la última ventana del
procedimiento de interacción con el usuario para el diseño con la metodología OPUS.
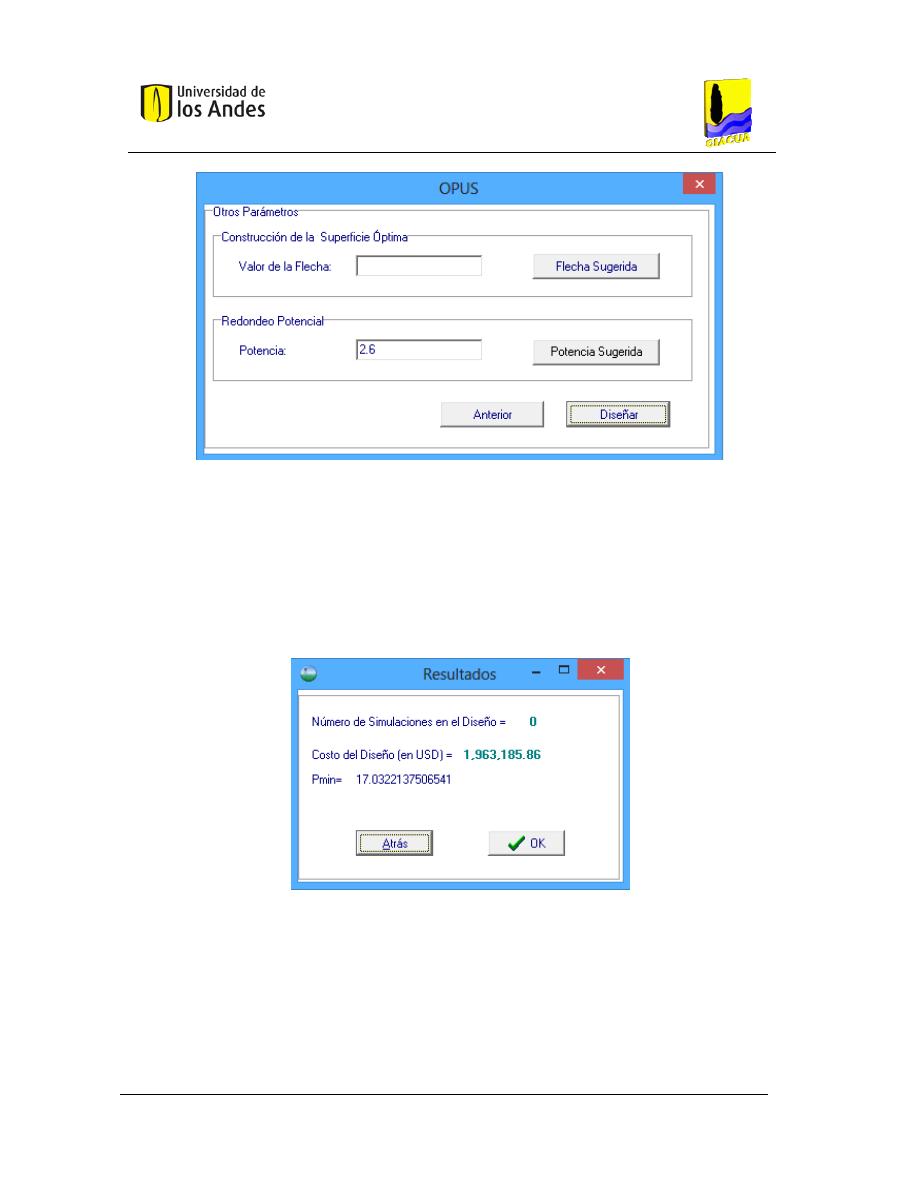
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
47
Figura 11 Ventana de para ingresar algunos parámetros del diseño.
La ventana que se observa en la Figura 11 permite ingresar el valor de la flecha o hacer que el
programa encuentre un valor sugerido para esta. Adicionalmente, en caso de elegir el redondeo
potencial, por defecto el valor es de 2.6 (derivado de ecuaciones hidráulicas); sin embargo este
valor puede ser modificado por el usuario.
Finalmente, luego de oprimir la opción Diseñar, emerge un ventana con los resultados del diseño.
Figura 12 Ventana de para ingresar algunos parámetros del diseño.
La Figura 12 muestra la ventana de resultados donde se resumen 3 aspectos generales del diseño
encontrado por la metodología: (1) Número de simulaciones en el Diseño, (2) Costo del Diseño (en
USD) y la Pmin (presión mínima). El primer y segundo resultado son fundamentales para comparar
la eficiencia de las metodologías de diseño y el último valor es indispensable para evaluar el
cumplimiento del requerimiento o restricción básica de cualquier RDAP, la presión mínima.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
48
3.
METODOLOGÍA PROPUESTA PARA LA APROXIMACIÓN DE DIÁMETROS EN
LA FASE FINAL DEL DISEÑO OPTIMIZADO DE REDES DE DISTRIBUCIÓN DE
AGUA
3.1. Metodología de inicio en caliente
La metodología de inicio en caliente (Hot Start) en este trabajo, combina el algoritmo basado en
hidráulica OPUS con una metaheurística Algoritmo Voraz (también nombrada en este documento
por su traducción en inglés como Greedy Algorithm). El conjunto de diámetros continuos
obtenidos a través de OPUS se utiliza como la configuración inicial de la red para ser post-
optimizado usando una técnica estocástica. La metaheurística probada en esta investigación ha
sido adaptada para el caso del diseño RDAP por Manuel A. Andrade; Doosun Kang; Christopher Y.
Choi; y Kevin Lansey (2013) y se llevó a cabo utilizando el programa informático: REDES 2013. Las
principales características del algoritmo incluido en este trabajo se describen a continuación.
3.2. Heurística de Postoptimization: Algoritmo Voraz
Teniendo en cuenta los resultados que arroja OPUS y al hacer un análisis detallado de las
diferencias entre los modelos obtenidos con diámetros discretos y diseños óptimos con diámetros
continuos, se encontró que las diferencias hidráulicas son una consecuencia de la restricción de
diámetro comercial. Esta restricción, normalmente plantea dificultades en el diseño de RDAP
como metodologías basadas en hidráulica tales como OPUS pues tienen pasos intermedios que
calculan diseños continuos teóricamente óptimos, que luego son completamente afectados por el
redondeo de los diámetros. Esto sucede porque el comportamiento hidráulico del sistema puede
cambiar drásticamente después de las modificaciones en los diámetros de las tuberías. En este
sentido, esta investigación implementa diseños obtenidos en la etapa final de la metodología
OPUS como un "Hot Start" para la metodología metaheurística conocida como Algoritmo Voraz o
"Greedy Algorithm". El uso de esta metahuristica se propone, con el objetivo de utilizar los
resultados obtenidos con criterios hidráulicos determinísticos presentes en la metodología OPUS.
Los resultados obtenidos en esta nueva etapa de la elaboración de la metodología basada en el
uso de diversos criterios para la optimización del diseño de RDAP, se presentan en las tablas
comparativas que representan los costos obtenidos, Índice de Resiliencia y las ejecuciones
hidráulicas (medición del esfuerzo computacional) para la obtención de tales costos. La
metodología propuesta se ha probado en diferentes problemas de referencia (Hanói, Balerma y
Taichung) y una cuarta red denominada R28, dando resultados muy cercanos a los registros
globales, con una diferencia aunque insignificante, mejor en relación con la metodología RAD
(redondeo, aumento y disminución) de OPUS. Además, el número de iteraciones disminuye
sustancialmente con respecto a la metodología del OPUS, lo que implica que la mejora de los
diseños basados hidráulicamente no requiere un gran esfuerzo computacional adicional para una
reducción en los costos.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
49
3.2.1. Definición
Un diseño de una RDAP casi óptima (llamado diseño original en este documento) logrado
mediante el uso del algoritmo basado en hidráulica OPUS; puede mejorar mediante la reducción
del valor de la función objetivo si existe al menos un tubo con un diámetro que puede ser reducido
sin violar alguna restricción impuesta por el original de diseño (ver Numeral 2.1). Sea el conjunto S,
que consta de tuberías que pueden ser individualmente disminuidas de tamaño sin violar estas
restricciones y contiene más de un elemento, entonces la mejor posible modificación al diseño
original se puede conseguir mediante la resolución del siguiente problema: encontrar el
subconjunto de tubos en S que, cuando sus diámetros se reducen en conjunto, produce la mayor
disminución en el valor de la función objetivo relativo al diseño original casi óptimo.
Al igual que el problema de diseño inicial, este es un problema combinatorio. Si el conjunto S
contiene n elementos, entonces el número total de posibles modificaciones serán la suma de cada
combinación de n e i, para i = 1,…, n. Para redes pequeñas, S puede contener sólo unos pocos
elementos (o ninguno), y la solución es trivial. Sin embargo, para redes de distribución de agua
potable verdaderas, un esquema de enumeración se hace inviable incluso para un conjunto de
tamaño modesto. Por lo tanto, la búsqueda de la mejor combinación de cambios requerirá
resolver un problema de optimización intensiva computacionalmente. Sin embargo, una buena
aproximación de la mejor solución puede lograrse rápidamente mediante el uso de un enfoque
heurístico que selecciona un tubo (k) en S, uno a la vez, y reduce su diámetro para determinar si al
hacerlo mejorará la solución. Este enfoque es conocido como un Algoritmo Voraz; a continuación
se propone una heurística de este tipo.
3.2.2. Hot Start: Redondeo solución OPUS
Como se anotó anteriormente esta metodología requiere de un diseño óptimo local discreto,
obtenido como resultado del redondeo de una solución óptima global en términos continuos
arrojada por la metodología OPUS. Con el fin de hacer el cambio de continuo a discreto de la
forma más sencilla y conservadora, se propone redondear los diámetros al siguiente diámetro
comercial y en caso de que dicho redondeo no cumpla con presión mínima, todos los diámetros
son aumentados al siguiente diámetro comercial respectivo a cada tubo. Este redondeo busca
conservar el dimensionamiento general de la red (proporción) y aumentar el espacio muestral
6
del
Algoritmo Voraz (mayor numero de combinaciones de reducción).
Los pasos del algoritmo de redondeo para el inicio en caliente del Algoritmo Voraz se describen a
continuación:
1) Ejecutar el Diagrama de Flujo 1: Redondeo aproximando al siguiente diámetro
comercial
6
el espacio muestral o espacio de muestreo consiste en el conjunto de todos los posibles
resultados individuales de un experimento aleatorio, en este caso el experimento aleatorio es
numerable y finito.
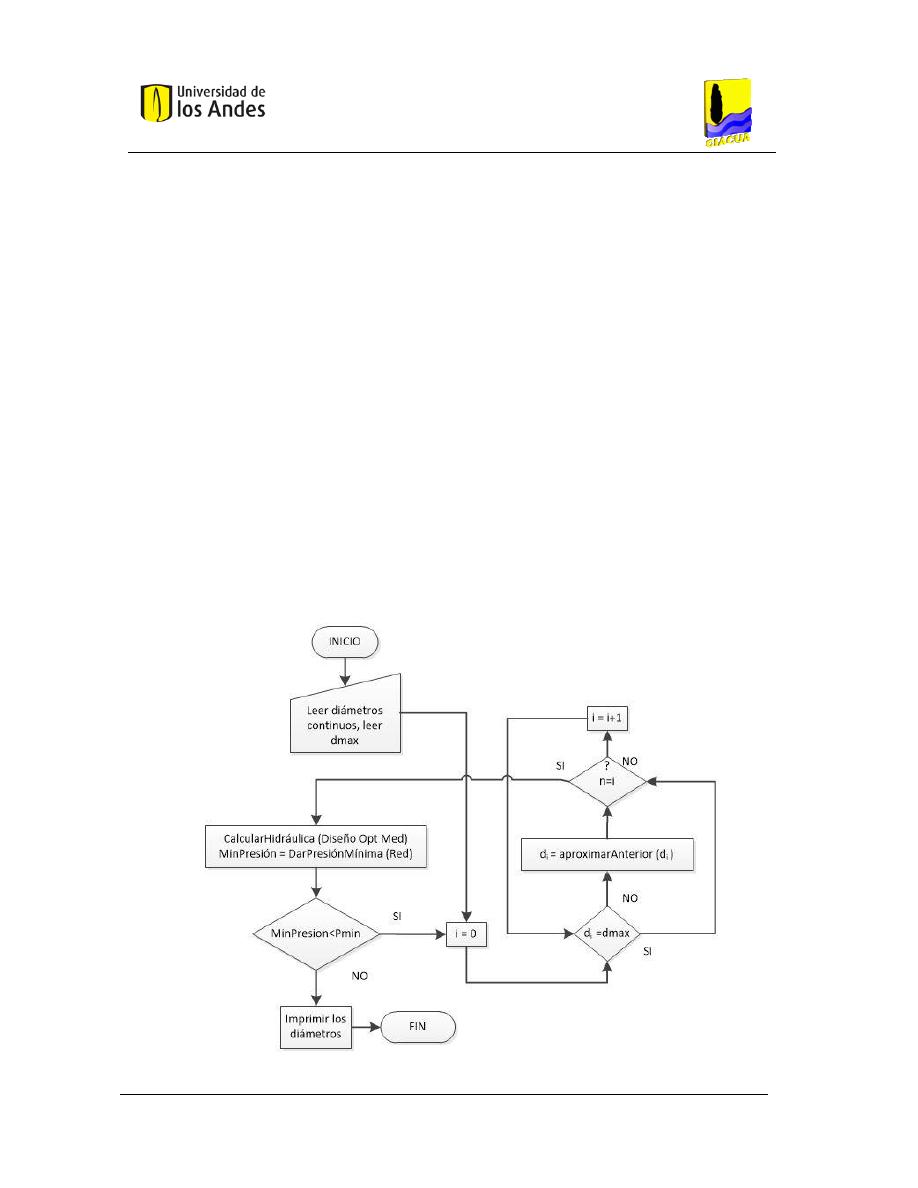
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
50
2) Leer la presión mínima (M.C.A) ingresada como parámetro por el usuario y leer el
diámetro comercial máximo.
3) Calcular la hidráulica (con el calculador hidráulico deseado por el usuario:
SparseSolver o Epanet) de la red actual y leer la presión mínima de dicha red.
4) Si la presión mínima de la red actual es menor que la presión mínima ingresada
como parámetro inicializar el proceso en i = 1, donde i corresponde a la posición de
cada tubo dentro de la serie. En caso de lo contrario ir al paso 8.
5) Leer el diámetro comercial siguiente al diámetro i. Si el
, se cambia el diámetro i por el diámetro comercial
siguiente, en caso de lo contrario se deja igual.
6) i = i + 1 (se pasa al siguiente tubo de la serie).
7) Si i es menor que NT (NT = número de tubos que conforman la serie), regresar al
Paso 5, de lo contrario, imprimir los diámetros de los tubos.
8) Fin del algoritmo.
El siguiente esquema permite visualizar el procedimiento que se acaba de describir.
Diagrama de flujo 6. Redondeo para Hot Star del Greedy Algorithm. Por el autor.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
51
3.2.3. Algoritmo Voraz o Greedy Algorithm
El objetivo del algoritmo es mejorar el diseño de una red de abastecimiento de agua obtenida
utilizando OPUS para tratar con el problema de optimización definido por Las ecuaciones (1), (2) y
(3).
La restricción del algoritmo es que sólo se diseñó para refinar el diámetro de los tubos; las
dimensiones o números de otros componentes de la red, tales como bombas, se deben especificar
por adelantado. El algoritmo puede ser utilizado en el análisis de las redes de abastecimiento de
agua con dimensiones realistas; sin embargo, la mejoría puede ser mínima si se aplica a redes que
implican sólo unos pocos componentes.
Considere dos juegos de tubos, S y T. La primera serie (S) contiene todos los tubos en una red
dada, con diámetros que pueden ser o no reducidos individuales sin dejar de cumplir las
restricciones de diseño impuestas anteriormente. El segundo conjunto (T) es un subconjunto de S
que consiste en tuberías que se puede reducir colectivamente sin violar las mismas limitaciones.
De acuerdo con la función objetivo, una solución óptima será el conjunto T que contiene los tubos
que, cuando sus diámetros disminuyen, proporcionarán la mayor reducción de costos. El general
Algoritmo Voraz para obtener T puede describirse en pseudocódigo de la siguiente manera:
1. Obtener las características del diseño original: costo, presión mínima e Índice de
Resiliencia.
2. Si la presión mínima de la red actual es mayor que la presión mínima ingresada como
parámetro ir a al paso 3, de lo contrario ir al paso 8.
3. Crear el conjunto T. Repetir los pasos a-d para cada tubo de la red.
a. Reducir el diámetro de la tubería actual por tamaño comercial menor.
b. Realizar un análisis hidráulico.
c. Si todos los nudos en la red satisfacen la restricción de presión mínima:
-
Añadir la tubería actual al subconjunto T
-
Obtener las siguientes características
7
de la red con el cambio: el costo, la
presión mínima, el Índice de Resiliencia y la potencia unitaria.
d. Devolver el diámetro de la tubería actual a su tamaño anterior.
4. Obtener los valores extremos (máximo y mínimo) de: el ahorro (resta entre el valor de la
red original del paso 1 y el valor de cada una de las redes obtenidas en el paso 2.c), la
presión mínima, la potencia unitaria y la diferencia absoluta de Índice de Resiliencia “IR”
7
En este estudio se tomaron en cuenta 4 características; sin embargo es posible adicionar o retirar otras
características.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
52
(valor absoluto entre el IR de la red original del paso 1 y el IR de cada una de las redes
obtenidas en el paso 2.c)
5. Identificar el mejor tubo candidato del conjunto T. Repetir los pasos a-d para cada tubo
del conjunto T.
a. Reducir el diámetro de la tubería actual por tamaño comercial menor.
b. Realizar un análisis hidráulico.
c. Obtener las siguientes características
8
de la red con el cambio: el costo, la presión
mínima, el Índice de Resiliencia y la potencia unitaria.
d. Calcular el ahorro de costo y la diferencia absoluta del Índice de Resiliencia.
e. Asignar un valor de decisión de la tubería actual sobre la base de una regla de
decisión (que se define en la sección siguiente).
f. Devolver el diámetro de la tubería actual a su tamaño anterior.
6. Reducir en un tamaño comercial el diámetro del tubo mejor candidato del conjunto S. (El
de mayor valor del paso 4.e)
7. Ir al paso 1 para crear una nueva conjunto S.
8. Imprimir los diámetros. Fin del algoritmo.
8
En este estudio se tomaron en cuenta 4 características, sin embargo es posible adicionar o retirar otras
características.
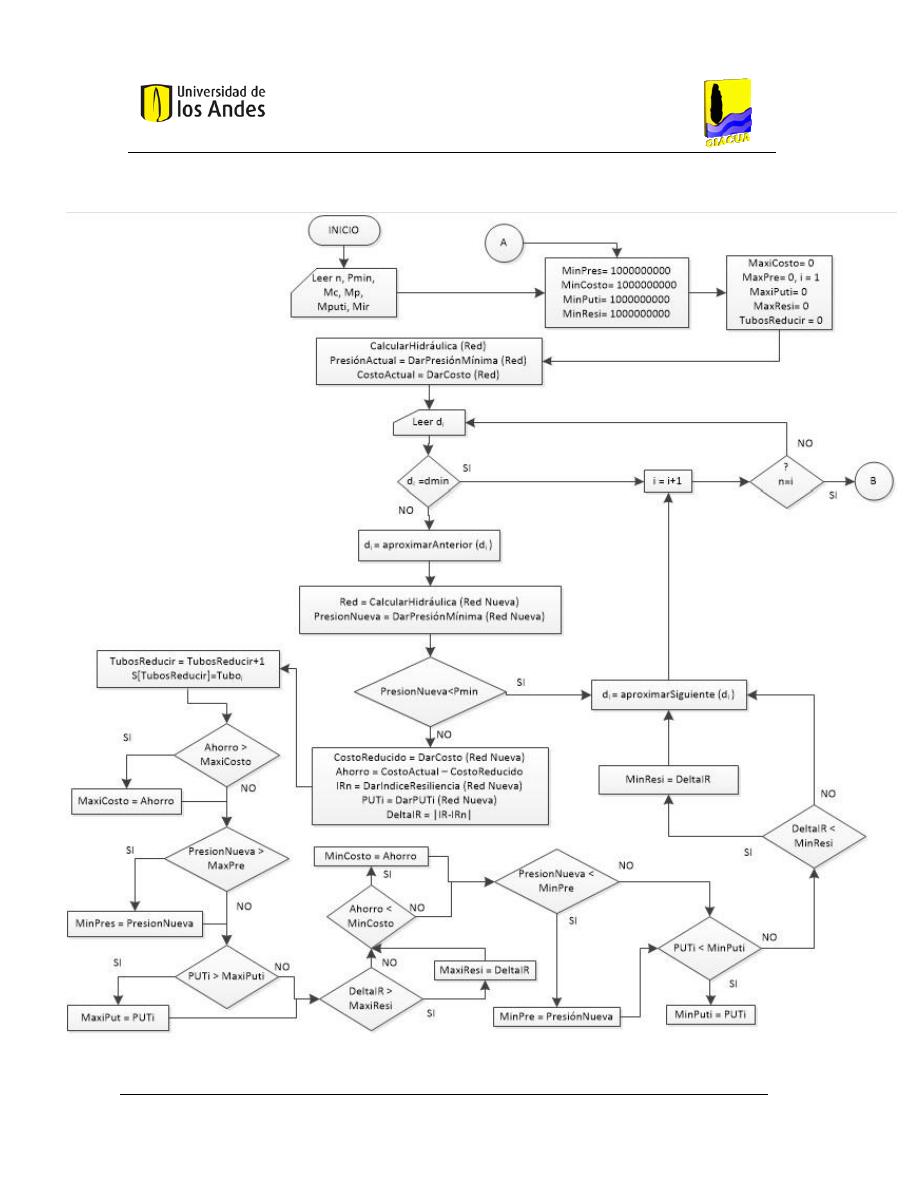
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
53
El siguiente esquema permite visualizar el procedimiento que se acaba de describir.
Diagrama de flujo 7.1. Greedy Algorithm. Pasos 1 al 4. Por el autor.
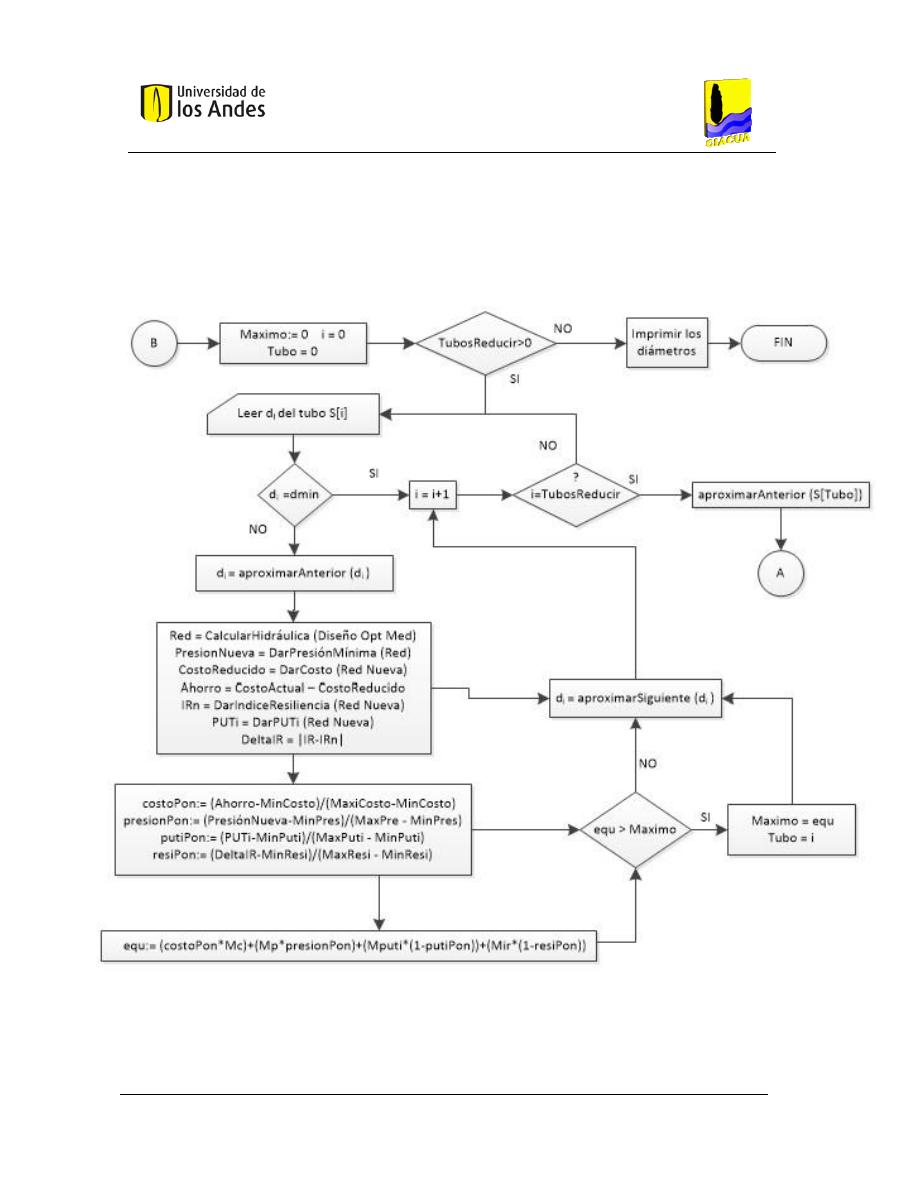
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
54
Diagrama de flujo 7.2. Greedy Algorithm. Pasos 5 al 8. Por el autor.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
55
La definición de una regla de decisión apropiada es el componente más crítico del algoritmo
debido a que conseguir una buena solución utilizando este método depende en gran medida de la
selección del mejor tubo candidato k S en cada etapa de decisión. Si mantener la presión mínima
permitida es la única limitación, el candidato ideal K en S debe tener cuatro características: (1)
debe proporcionar el mayor ahorro después de reducir su diámetro por uno comercial, (2) debe
tener las menores reducciones de la presión, (3) la menor potencia unitaria y (4) el menor cambio
en el Índice de Resiliencia; encontrar un tubo con todos los atributos es poco probable,
especialmente si el tubo se encuentra en una línea del nudo crítico. Por lo tanto, teniendo en
cuenta el equilibrio entre estos cuatro atributos, se debe tener cuidado al definir la regla de
decisión para el Algoritmo Voraz. Los criterios (3) y (4) que son características hidráulicas, se
adicionaron con el fin de analizar su incidencia en el algoritmo.
3.2.4. Regla de decisión ponderada
Para implementar el algoritmo anterior, es necesario definir un regla de decisión que puede medir
el mérito relativo de una tubería candidata k en comparación con todos los otros elementos en S.
Suponiendo que que la presión es la única restricción, la regla de decisión puede basarse en el
equilibrio entre: (1) la reducción de costos obtenida y (2) la disminución de la presión crítica
9
(causada por la disminución del diámetro de K); adicionalmente se incluyen los conceptos de (3)
Resiliencia y (4) Potencia Unitaria PuTI, que serán explicados a continuación:
Resiliencia
Existen diferentes indicadores para cuantificar la confiabilidad de una RDAP; uno de los más
utilizados actualmente por los investigadores a nivel mundial es el Índice de Resiliencia -Ir- (Todini,
2000). El creador de este índice, Ezio Todini, lo define de la siguiente manera (Todini, 2008):
“La resiliencia es la capacidad intrínseca que tiene una RDAP para superar fallas
repentinas y se mide como la proporción entre el excedente de potencia que es
entregado a los usuarios y la máxima potencia que puede ser disipada en la red
cuando se cumplen exactamente los criterios y condiciones de diseño. El Índice
de Resiliencia proporciona una medida general de la redundancia del sistema: un
mayor valor del Índice de Resiliencia corresponde a una mayor redundancia.”
9
La presión critica hace referencia a la presión en el nudo crítico, es decir el de menor presión.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
56
El Índice de Resiliencia se calcula como:
∑
(
)
[∑
∑
] ∑
donde,
: Demanda actual del nudo i.
: Altura piezométrica requerida en los nudos de demanda.
: Altura mínima piezométrica requerida en los nudos de demanda.
: Caudal de entrada suministrado por el embalse i.
: Altura de entrada suministrado por el embalse i.
: Potencia por unidad de peso suministrada por la bomba i.
: Número de bombas propias de la red.
Potencia Unitaria PUTi
Se define como la altura piezométrica gastada en una tubería dada, es decir, la diferencia de
alturas piezométricas entre los nudos que conforman ese segmento de tubería, multiplicada por el
caudal que está pasando por ese tubo:
(
)
donde,
: Demanda actual del nudo i.
: Altura piezométrica requerida en el nudos inicial del tubo i.
: Altura piezométrica requerida en el nudos final del tubo i.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
57
La definición de una norma de este tipo se puede lograr mediante la asignación de los pesos
relativos a cada tubo candidato k S. Si, por ejemplo, k es el tubo que produce el más alto ahorro
de costo (
) cuando se reduce su diámetro, entonces k recibe un peso relativo de
. Por el contrario, si k es la tubería que suministra el ahorro más bajo
),
entonces la tubería k recibe un peso relativo de
. De este modo el peso relativo premia el
mayor ahorro por la reducción de la tubería k y castiga el peor ahorro.
Del mismo modo, si la reducción del diámetro de la tubería k produce la menor reducción de
presión o la presión más alta
como consecuencia, entonces k recibe un peso relativo de
. Pero si la reducción del diámetro de la tubería k produce la mayor reducción de la
presión o la presión más baja
, entonces k recibe un peso relativo del
. De esta manera
el peso relativo premia la mayor presión mínima de la red por la reducción de la tubería k y castiga
la menor presión mínima.
Así mismo, si la reducción del diámetro de la tubería k produce el mayor reducción de potencia
unitaria o la presión más baja
como consecuencia, entonces k recibe un peso relativo de
. Pero si la reducción del diámetro de la tubería k produce la menor reducción de la
potencia unitaria o la potencia unitaria más alta
, entonces k recibe un peso relativo del
. De esta manera el peso relativo premia la potencia unitaria de la red por la reducción
de la tubería k y castiga la mayor potencia unitaria.
Análogamente, si la reducción del diámetro de la tubería k produce el menor cambio del Índice de
Resiliencia con respecto del diseño original o el cambio más pequeño
como
consecuencia, entonces k recibe un peso relativo de
. Pero si la reducción del diámetro
de la tubería k produce el mayor cambio del Índice de Resiliencia con respecto del diseño original
o el cambio más grande
, entonces k recibe un peso relativo del
. De esta
manera el peso relativo premia el mínimo cambio en el Índice de Resiliencia, por la reducción de la
tubería k, con respecto al modelo original y castiga la de mayor cambio. Por lo anterior no se tiene
en cuenta si el cambio beneficia o no la redundancia de la red.
Para diferenciar la importancia dada a cada factor en la regla de decisión, se definen cuatro
parámetros que suman 1:
,
y
, donde
[0,1] es un multiplicador para
[0,1] es un multiplicador para
[0,1] es un multiplicador para
y
[0,1] es un multiplicador para
. Cabe aclarar que como lo muestra la Ecuación 14 la suma de
los parámetros debe ser igual a 1.
Ecuación 14

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
58
Una regla de decisión conveniente para el Algoritmo Voraz, se define a continuación: "Seleccionar
el tubo k S con el valor de decisión más alto
", donde
es determinado por la suma
ponderada de los cuatro factores:
Ecuación 15
[
]
[
]
[
]
[
]
donde
= ahorro obtenido mediante la reducción de tubo k;
= presión en el nudo
crítico o presión mínima después de la modificación de la tubería k;
es la potencia unitaria
de la red después de la modificación de la tubería k;
= diferencia de Índice de
Resiliencia obtenida mediante la reducción de tubo k.
y
=
respectivamente son el ahorro máximo y mínimo de costos que pueden resultar de la reducción
de cualquier tubería del conjunto S,
y
= respectivamente son la presión máxima y
mínima que pueden resultar de la reducción de cualquier tubería del conjunto S,
y
= respectivamente son la potencia unitaria máxima y mínima que pueden resultar de la
reducción de cualquier tubería del conjunto S y
y
= respectivamente son
el cambio de resiliencia máxima y mínima respecto al diseño original que pueden resultar de la
reducción de cualquier tubería del conjunto S.
En la ecuación 15, un valor de decisión
se asigna al candidato ideal, y un valor de 0 para
el peor posible candidato, mientras que todos los otros tubos reciben un peso de entre 0 y 1. La
tubería que combina el mayor ahorro, la menor reducción de presión en el nudo crítico, la menor
potencia unitaria y el menor cambio en el Índice de Resiliencia recibe el valor más alto de decisión
(
) en S y es añadido a la solución prevista T (paso 3 del algoritmo).
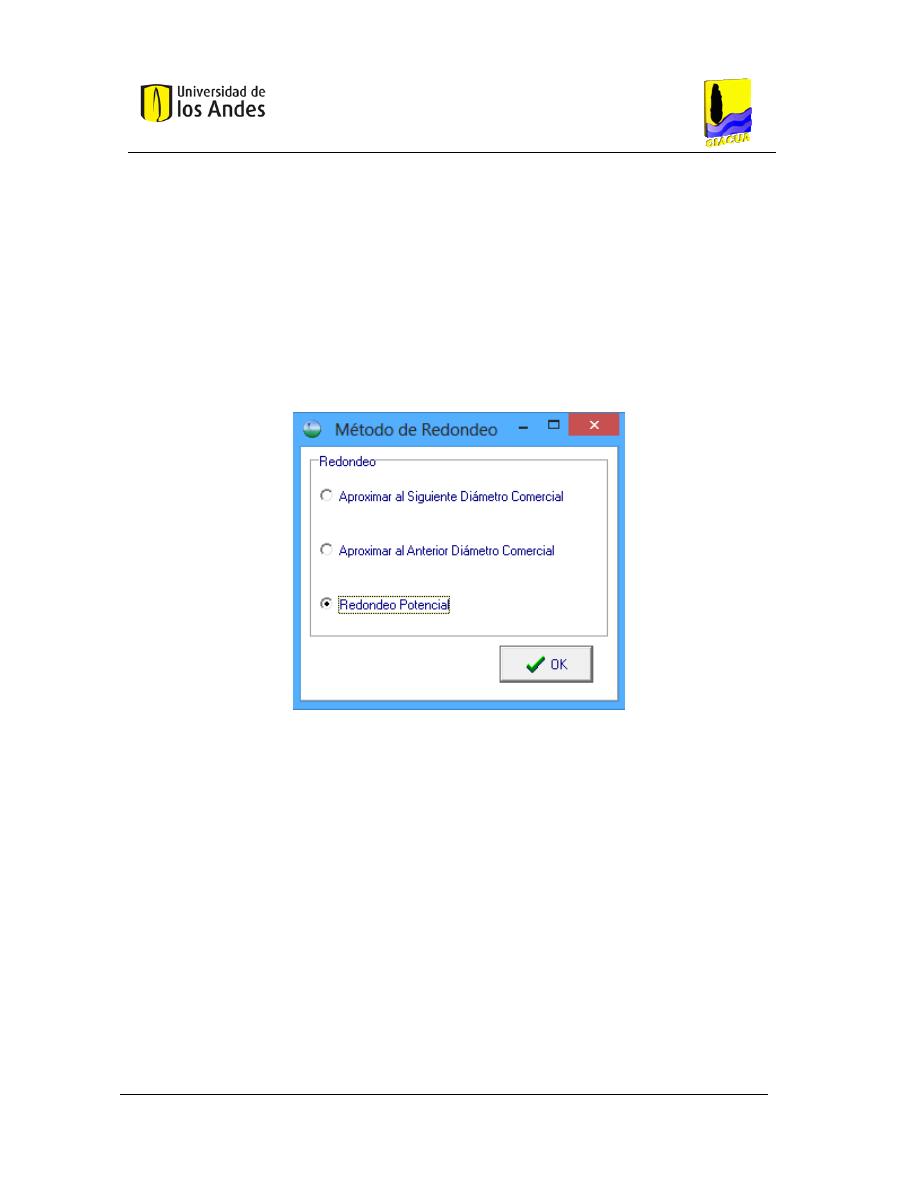
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
59
4. EVALUACIÓN DEL DESEMPEÑO DE LA METODOLOGÍA PROPUESTA
4.1. Uso de la metodología propuesta desarrollada para OPUS en el
programa REDES
El único cambio con respecto al breve manual de uso del Numeral 2.7.11 es en el uso de la opción
“Discretos” del cuadro “Diámetros” en la venta emergente de “OPUS”. Aunque como se observa
en la Figura 13, las opciones siguen siendo las mismas:
Figura 13 Ventana de para ingresar el método de aproximación.
Al dar clic en la opción “Aproximar al Siguiente Diámetro Comercial” aparece una nueva ventana
que se ve así:
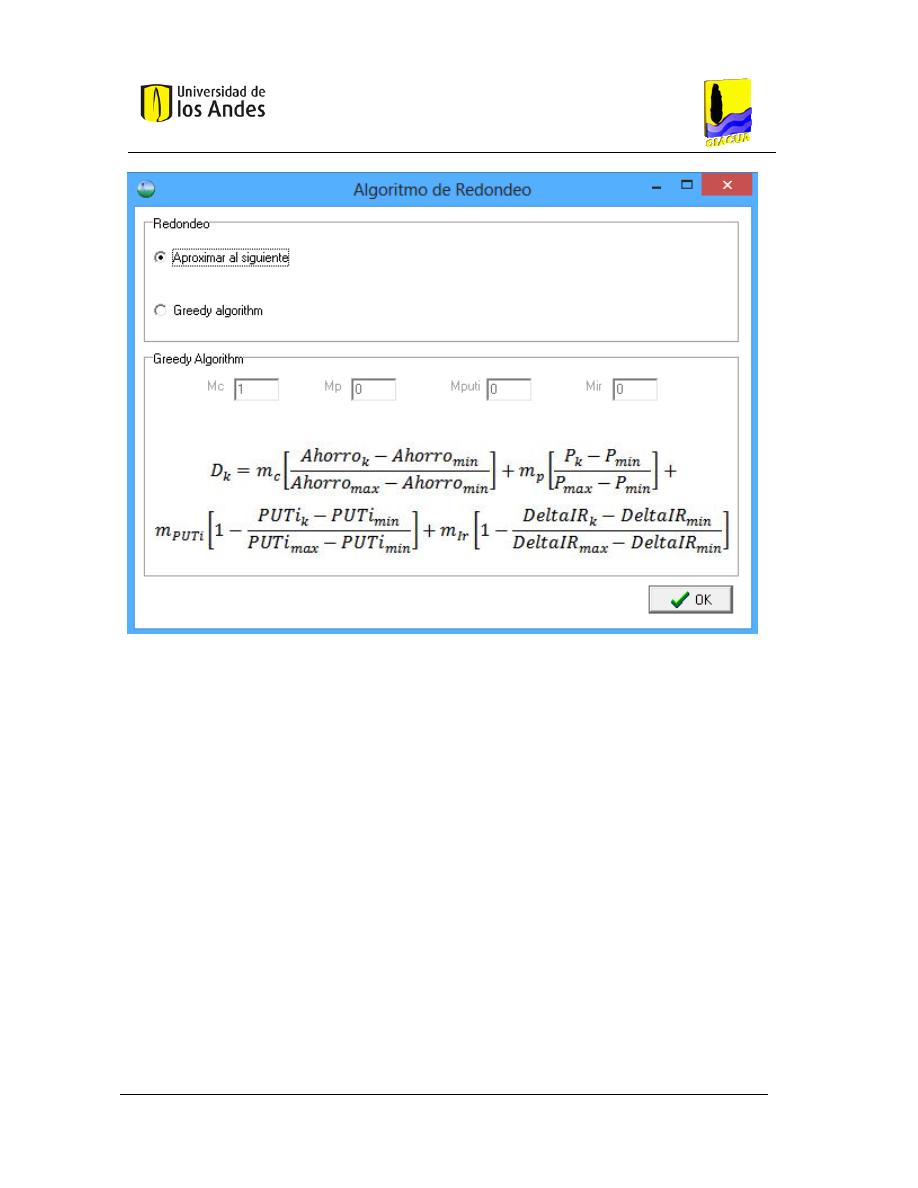
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
60
Figura 14 Ventana de para ingresar elegir entre el redondeo simple al siguiente o el Algoritmo Voraz
La Figura 14 muestra que el usuario puede elegir simplemente “Aproximar al siguiente” que
ejecuta la metodología de RAD de OPUS explicada en el Numeral 2.7.7. Se decidió adicionar la
opción del Algoritmo Voraz partiendo de la ventana de redondeo, pues es de este redondeo que el
algoritmo inicia su optimización. Adicionalmente, no se desea saturar las ventanas existentes con
más opciones, pues puede llegar a confundir al usuario.
Por otro lado si el usuario elige la opción “Greedy Algorithm” la ventana tendrá algunos cambios
que se muestran en la Figura 15 a continuación.
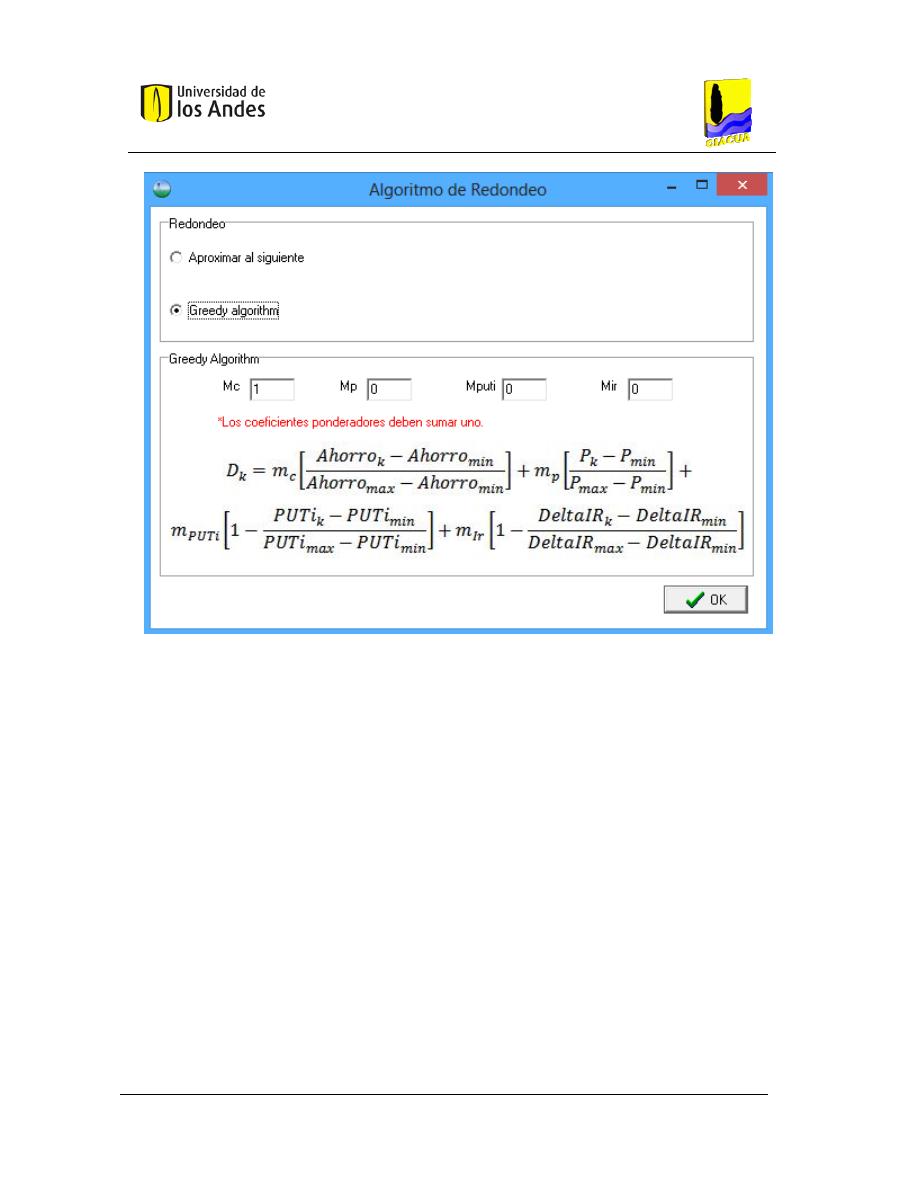
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
61
Figura 15 Ventana de para ingresar los parámetros del Algoritmo Voraz “Greedy Algorithm”.
Al elegir esta opción, el usuario puede cambiar los pesos de los parámetros ponderadores
,
y
así mismo se le recuerda que los ponderadores deben sumar uno y se muestra la
regla de decisión con el fin de que el usuario entienda las consideraciones explicadas en el
Numeral 3.2.4 sobre la tubería ideal que combina el mayor ahorro, la menor reducción de presión
en el nudo crítico, la menor potencia unitaria y el menor cambio en el Índice de Resiliencia, la cual
recibe el valor más alto de decisión (
).
Toda la metodología Hot Start se validó con la ayuda de 3 redes de referencia: Hanoi, Balerma y
Taichung, además de una cuarta red conocido como R28, que serán presentados a continuación.
Cada uno de estos RDAP fueron diseñadas utilizando la metaheurística explicada anteriormente,
una vez que se aplicó la metodología OPUS. Con el fin de determinar cuáles de los 4 factores
(costo, presión, Índice de Resiliencia y potencia unitaria) son significativos para el algoritmo se
realizaron pruebas haciendo combinaciones de 2, 3 y 4 factores, haciendo cambios en pasos de 0.2
para el peso de cada uno de los parámetros. Dichas combinaciones se muestren a continuación:
En adelante se hará referencia a los parámetros ponderadores
,
y
respectivamente así: Mc, Mp, Mputi, Mir.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
62
Dos factores
Dado que se tiene un conjunto de cuatro factores y se quiere configurar en grupos de a dos
factores es útil hacer uso de la fórmula de coeficiente binomial:
(
)
Por lo anterior se pueden formar 6 subconjuntos de dos factores; dichos conjuntos y sus
respectivos parámetros con la variación de sus pesos (en pasos de 0.2) se muestran a
continuación:
Mc
Mp
Mc
Mputi
Mc
Mir
Mp Mputi Mp
Mir Mputi Mir
0
1
0
1
0
1
0
1
0
1
0
1
0.2
0.8
0.2
0.8
0.2
0.8
0.2
0.8
0.2
0.8
0.2
0.8
0.4
0.6
0.4
0.6
0.4
0.6
0.4
0.6
0.4
0.6
0.4
0.6
0.6
0.4
0.6
0.4
0.6
0.4
0.6
0.4
0.6
0.4
0.6
0.4
0.8
0.2
0.8
0.2
0.8
0.2
0.8
0.2
0.8
0.2
0.8
0.2
1
0
1
0
1
0
1
0
1
0
1
0
Tabla 1. Escenario dos factores: Subconjuntos de factores y pesos de los factores.
Para este caso se hicieron 36 pruebas en cada una de las 4 redes.
Tres factores
Dado que se tiene un conjunto de cuatro factores y se quiere configurar en grupos de a tres
factores es útil hacer uso de la fórmula de coeficiente binomial:
(
)
Por lo anterior se pueden formar seis subconjuntos de tres factores, dichos conjuntos y sus
respectivos parámetros con la variación de sus pesos (en pasos de 0.2) se muestran a
continuación:
Mc
Mp
Mputi
Mc
Mp
Mir
Mc
Mp
Mir
Mp
Mpu
Mir
0.2
0.6
0.2
0.2
0.6
0.2
0.2
0.6
0.2
0.2
0.6
0.2
0.2
0.4
0.4
0.2
0.4
0.4
0.2
0.4
0.4
0.2
0.4
0.4
0.2
0.2
0.6
0.2
0.2
0.6
0.2
0.2
0.6
0.2
0.2
0.6
0.4
0.4
0.2
0.4
0.4
0.2
0.4
0.4
0.2
0.4
0.4
0.2
0.4
0.2
0.4
0.4
0.2
0.4
0.4
0.2
0.4
0.4
0.2
0.4
0.6
0.2
0.2
0.6
0.2
0.2
0.6
0.2
0.2
0.6
0.2
0.2
Tabla 2. Escenario tres factores: Subconjuntos de factores y pesos de los factores.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
63
Para este caso se hicieron 24 pruebas en cada una de las 4 redes.
Cuatro factores
Para este caso se forma un único conjunto con cuatro factores, dicho conjunto y sus respectivos
parámetros con la variación de sus pesos (en pasos de 0.2) se muestran a continuación:
Mc
Mp
Mputi
Mc
0.2
0.4
0.2
0.2
0.2
0.2
0.4
0.2
0.2
0.2
0.2
0.4
0.4
0.2
0.2
0.2
Tabla 3. Escenario cuatro factores: Subconjuntos de factores y pesos de los factores.
Para este caso se hicieron 4 pruebas en cada una de las 4 redes.
Finalmente cabe resaltar que las 64 (36+24+4) pruebas con diferentes parámetros y diferentes
pesos de dichos parámetros, se hicieron para cada una de las 4 redes patrón y para cada uno de
los 2 calculadores hidráulicos disponibles en el programa REDES 2013: SparseSolver y Epanet. Lo
anterior se traduce en un total de 512 pruebas del Algoritmo Voraz.
Sin embargo, dado que el calculador hidráulico SparseSolver tiene una limitación de capacidad de
memoria no se ejecutaron pruebas para le red Balerma (la red más grande de las testeadas) con
este calculador; por otro lado que el tiempo de ejecución es muy elevado para redes grandes con
el calculador Epanet no se realizaron pruebas de dos factores para la red Balerma, pues además,
dentro de las conclusiones de este trabajo se evidencia que las pruebas de dos factores no son las
ideales.
Lo anterior se traduce en un total de 400 pruebas que resultan en una población ideal para
concluir sobre la significancia de los factores en el algoritmo y para concluir acerca de la
efectividad del mismo.
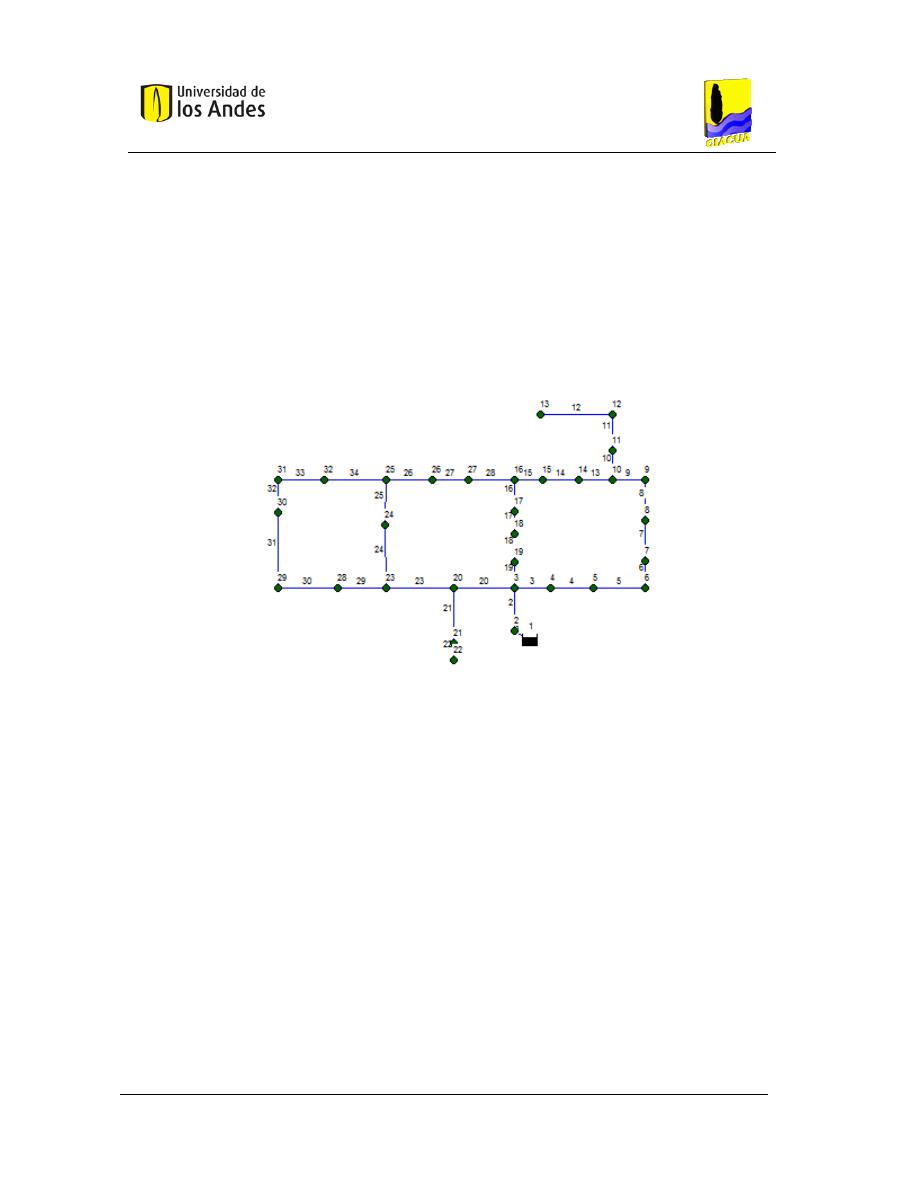
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
64
4.2. Red Hanoi
La red de Hanoi fue presentado por primera vez por Fujiwara y Khang (1990). La ecuación de
altura-pérdida comúnmente utilizado es la de Hazen-Williams con un coeficiente de rugosidad de
130, la presión mínima para el escenario de diseño es de 30 m y los costos de las tuberías se
pueden calcular utilizando una función potencial del diámetro con un coeficiente de unidad de US
$ 1,1 / m para pulgadas (0,00859295 para milímetros), y un exponente de 1,5. Los tubos
disponibles comercialmente son: 12, 16, 20, 24, 30 y 40 pulgadas. La red está formada por 34
tubos y 31 nudos configurados en 3 circuitos. Todo el sistema se suministra por 1 embalse con una
carga constante de 100 m. La topología de la red se presenta en la Figura 16.
Figura 16 RDAP Hanoi. Las etiquetas muestran los números de identificación de las tuberías y nudos.
En los anexos se presentan los todos los parámetros de la prueba para cada uno de los escenarios
posibles en la metaheurística propuesta, así como los valores específicos que dieron las soluciones
de costo mínimo. Los resultados obtenidos para esta red se presentan en la Tabla 4 en
comparación con los costos obtenidos a través del OPUS; no se tiene en cuenta el registro mundial
debido a que en el CIACUA regularmente se hacen pruebas adicionando un tubo comercial de 50
pulgadas pues es significativa la reducción del costo con respecto al planteamiento original del
problema. Para tenerlo en consideración dicho record fue obtenido por Kadu (2008) que encontró
un costo en miles de dólares de $6.056.
Los resultados de la Tabla 4 muestran que respecto al resultado de RAD-OPUS en general se
presenta un aumento en los costos, un aumento en el Índice de Resiliencia y una disminución del
número de iteraciones, para los mejores resultados obtenidos cada uno de los 3 escenarios
analizados (2,3 y 4 factores). Cabe resaltar que los mejores resultados en cuanto a costo se
obtuvieron para los escenarios de 2 y 3 factores.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
65
Costo
(M)
Iteraciones
Presión
Mínima
(m)
IR
Diferencia
de costo
con OPUS
Diferencia
de IR costo
con OPUS
OPUS by
Saldarriaga et al.
(2012)
$5.540
83
30.04
0.369
N/A
N/A
Algoritmo Voraz 2
parámetros
$5.580
30
30.69
0.369
0.7%
0.00%
Algoritmo Voraz 3
parámetros
$5.580
28
30.88
0.419
0.7%
13.55%
Algoritmo Voraz 4
parámetros
$5.600
28
30.01
0.415
1.1%
12.47%
Tabla 4. Resultados obtenidos para la red Hanoi.
4.3. Red Balerma
Balerma corresponde a un RDAP de un distrito de riego en Almería, España. Fue introducido por
primera vez por Reca y Martínez (2006). La expresión de pérdida de altura piezométrica utilizada
es la ecuación de Darcy-Weisbach. Los diámetros de tubería disponibles comercialmente para su
diseño se fabrican exclusivamente en PVC, con una rugosidad absoluta de 0,0015 mm. La presión
mínima permitida es de 20 m y tiene 10 tubos disponibles en el mercado cuyos costos unitarios
aparecen en parejas (diámetro en mm, costo en € / m): 113, 7,22; 126,6, 9,1; 144,6, 11,92; 162,8,
14,84; 180,8, 18,38; 226.2, 28.6, 285, 45,39 y 361,8, 76,32. Cuenta con un total de 454 tubos y 443
nudos de consumo que son suministrados por 4 embalses. La topología de la red se presenta en la
Figura 17.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
66
Figura 17 RDAP Balerma.
En los anexos se presentan los todos los parámetros de la prueba para cada uno de los escenarios
posibles en la metaheurística propuesta, así como los valores específicos que dieron las soluciones
de coste mínimo. Los resultados obtenidos para esta red se presentan en la Tabla 5 en
comparación con los costos obtenidos a través del OPUS y con el registro mundial.
Costo
(M)
Iteraciones
Presión
Mínima
(m)
RI
Diferencia de
costo con el
record
Diferencia
de IR con
el record
Diferencia
de costo
con OPUS
Diferencia
de IR costo
con OPUS
World Record by
Tolson (2009)
€ 1.940
30'000,000
N/A
0.308
N/A
N/A
N/A
N/A
OPUS by
Saldarriaga et al.
(2012)
€ 2,104
948
20.00
0.387
8.5%
25.65%
N/A
N/A
Algoritmo Voraz
3 parámetros
$2,076
153
20.01
0.402
7.0%
30.52%
-1.3%
3.88%
Algoritmo Voraz
4 parámetros
$2,076
155
20.01
0.398
7.0%
29.22%
-1.3%
2.84%
Tabla 5. Resultados obtenidos para la red Balerma.
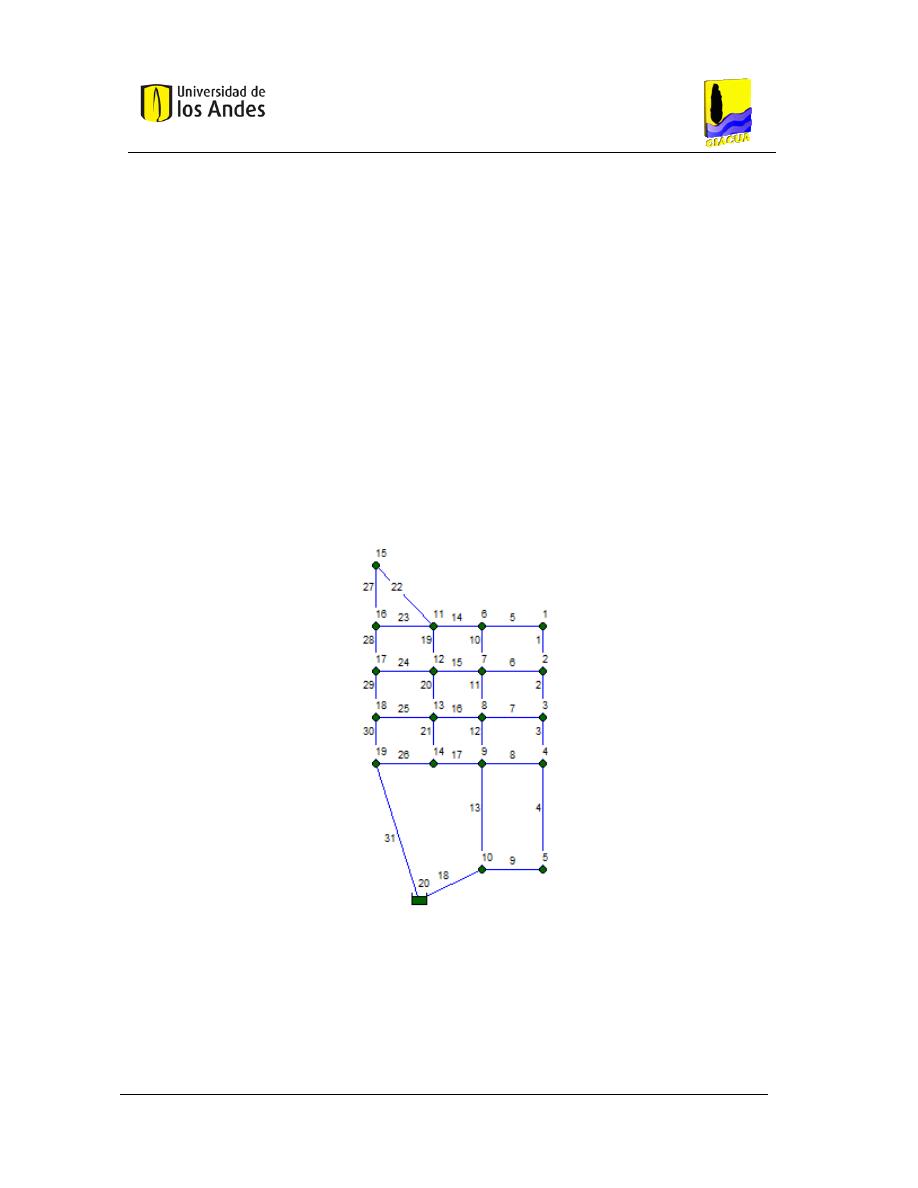
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
67
Los resultados de la Tabla 5 muestran que respecto al resultado de RAD-OPUS en general se
presenta una disminución en los costos, un aumento en el Índice de Resiliencia y una disminución
del número de iteraciones, para los mejores resultados obtenidos cada uno de los 2 escenarios
analizados (3 y 4 factores). Cabe resaltar que el mejor resultado en cuanto a costo se obtuvo para
el escenario de 3 factores.
4.4. Red Taichung
La red Taichung fue presentada por primera vez por Sung et al. (2007) y corresponde a una RDAP
situada en Taichung, Taiwán. La topología de la red se compone de 12 bucles formados por 31
tubos y 20 nudos, que son suministrados por un único depósito con altura de 113,98 m. Para su
diseño hay 13 diámetros de tubería disponibles comercialmente, cuyos costos unitarios aparecen
en parejas (diámetro en mm, el costo en dólares NT / m): 100, 860, 150, 1160, 200, 1470; 250,
1700; 300, 2080; 350, 2640; 400, 3240; 450, 3810; 500, 4400; 600, 5580; 700, 8360; 800, 10 400, y
900, 12800. La ecuación de la pérdida de altura piezométrica utilizada es la de Hazen-Williams con
un coeficiente de rugosidad de 100 y la presión mínima para el escenario de diseño es de 15 m. La
topología de la red se presenta en la Figura 18.
Figura 18 RDAP Taichung
En los Anexos Balerma se presentan los todos los parámetros de la prueba para cada uno de los
escenarios posibles en la metaheurística propuesta, así como los valores específicos que dieron las
soluciones de coste mínimo. Los resultados obtenidos para esta red se presentan en la Tabla 6 en
comparación con los costos obtenidos a través del OPUS y con el registro mundial.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
68
Los resultados de la tabla 6 muestran que respecto al resultado de RAD-OPUS en general se
presenta una disminución en los costos, en 2 casos un aumento en el Índice de Resiliencia y una
disminución del número de iteraciones, para los mejores resultados obtenidos cada uno de los 3
escenarios analizados (2, 3 y 4 factores). Cabe resaltar que el mejor resultado en cuanto a costo se
obtuvo para el escenario de 3 factores.
Costo
(M)
Iteraciones
Presión
Mínima
(m)
RI
Diferencia de
costo con el
record
Diferencia
de IR con
el record
Diferencia
de costo
con OPUS
Diferencia
de IR costo
con OPUS
World Record by
Sung et al. (2007)
$ 8.774
74500
N/A
0.212
N/A
N/A
N/A
N/A
OPUS
$ 8.936
77
15.45
0.232
1.8%
9.43%
N/A
N/A
Algoritmo Voraz
2 parámetros
$ 8.857
15
15.03
0.275
0.9%
29.72%
-0.9%
18.53%
Algoritmo Voraz
3 parámetros
$ 8.813
18
15.12
0.227
0.4%
7.08%
-1.4%
-2.16%
Algoritmo Voraz
4 parámetros
$ 8.922
21
15.21
0.201
1.7%
-5.19%
-0.2%
-13.36%
Tabla 6. Resultados obtenidos para la red Taicung.
4.5. Red R28
R28 es un RDAP hipotética creada con fines de investigación en el Centro de Investigaciones en
Acueductos y Alcantarillados (CIACUA) de la Universidad de Los Andes en Bogotá, Colombia. La
topología de la red se compone de 28 circuitos formados por 67 tubos y 39 nudos que son
suministrados por un solo depósito, con una altura de 40 m. Todos los nudos están a la misma
altura, excepto para el depósito que está a 15 m por encima. Esta red tiene la característica de
tener una demanda centrada. La pérdida de altura piezométrica se calcula con la ecuación de
Darcy-Weisbach y el material de la tubería para toda la red es de PVC, con una rugosidad absoluta
de 0,0015 mm. La presión mínima para el escenario de diseño es de 15 m. El sistema cuenta con
19 diámetros disponibles , que son : 50 , 75 , 100 , 150 , 200 , 250 , 300 , 350 , 400 , 450 , 500 , 600
, 750 , 800 , 1.000 , 1.200 , 1.400 , 1.500 y 1.800 mm . Costo de las tuberías en dólares por metro
($ / m) se puede calcular utilizando una función potencial del diámetro (mm) con un coeficiente de
0,015 y un exponente de 1,45.
Las demandas de esta red se enumeran en orden de número de identificación de nudo: 3 , 7, 8 , 7,
4 , 12, 21 , 24, 22 , 8, 10 , 28, 31 , 27, 15 , 24, 29 , 33, 30 , 10 , 11 , 31 , 34 , 30 , 23 , 27 , 31 , 28 , 10 ,
9 , 25 , 27 , 24 , 13 , 6 , 11 , 12 , 11 , 4 L / seg .

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
69
La longitud de los tubos se enumeran por orden de número de identificación de la tubería: 80 ,
150, 100 , 120, 100 , 120, 100 , 150, 80 , 200, 120 , 100, 150 , 80, 180 , 120, 100 , 150, 80 , 220 ,
120 , 100 , 150 , 80 , 200 , 120 , 100 , 150 , 80 , 180 , 120 , 100 , 150 , 80 , 150 , 120 , 100 , 150 , 80 ,
150 , 200 , 220 , 180 , 100 , 200 , 180 , 100 , 150 , 200 , 180 , 180 , 200 , 220 , 100 , 150 , 200 , 180 ,
180 , 200 , 220 , 100 , 150 , 200 , 180 , 180 , 200 , 220 metros . La topología de la red se presenta
en la Figura 18.
Figura 19 RDAP R28. Las etiquetas muestran los números de identificación de tuberías y nodal.
En los anexos se presentan los todos los parámetros de la prueba para cada uno de los escenarios
posibles en la metaheurística propuesta, así como los valores específicos que dieron las soluciones
de costo mínimo. Los resultados obtenidos para esta red se presentan en la Tabla 7 en
comparación con los costes obtenidos a través del OPUS y con el registro mundial.
Costo (M)
Iteraciones
Presión
Mínima
(m)
RI
Diferencia
de costo
con OPUS
Diferencia
de IR costo
con OPUS
OPUS by
Saldarriaga et al.
(2012)
$ 149,833
77
15.00
0.384
N/A
N/A
Algoritmo Voraz
2 parámetros
$ 150.516
38
14.97
0.387
0.5%
0.78%
Algoritmo Voraz
3 parámetros
$ 149.262
41
15.33
0.357
-0.4%
-7.03%
Algoritmo Voraz
4 parámetros
$ 149.586
21
15.21
0.4
-0.2%
4.17%
Tabla 7. Resultados obtenidos para la red R28.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
70
Los resultados de la Tabla 7 muestran que con respecto al resultado de RAD-OPUS en general se
presenta una disminución en los costos en 2 casos, un aumento en el Índice de Resiliencia y una
disminución del número de iteraciones, para los mejores resultados obtenidos cada uno de los 3
escenarios analizados (2, 3 y 4 factores). Cabe resaltar que el mejor resultado en cuanto a costo se
obtuvo para el escenario de 3 factores.
4.6. Relación de los resultados
En primer lugar, con el fin de tener certeza en que las conclusiones respecto al funcionamiento del
algoritmo estarían bien validadas, se realizaron pruebas de las metodología usada hasta ahora en
el programa REDES, es decir la el redondeo, aumento y disminución “RAD”. Adicionalmente, era
indispensable conocer los mejores parámetros de entrada para cada red para así asegurar los
mejores resultados. Dichos parámetros son:
-
Ecuación de recálculo de la flecha.
-
Distribución óptima de presiones (DOC).
-
Valor de la flecha.
De manera general se encontró que para todas las redes lo mejor es elegir la opción “Presión
Promedio” para el recalculo de la flecha y una distribución óptima de presiones con “Mayor
relación B/C” y DOC (“Normal”). Para cada red se encontró un valor de flecha óptimo específico;
dicho valor no se analiza en este estudio.
Finalmente los parámetros ingresados para cada red están disponibles en la Tabla 8.
Coeficiente
in
mm
exponente
Pmin
m.c.a
Flecha
HW
Hanoi
1.1
0.008592947
1.5
30
0.1355
130
Balerma
0.00041245
2.0618
20
0.1848
N/A
R28
0.015
1.45
15
0.0815
N/A
Taichung
1.9482
1.2571
15
0.1007
100
Tabla 8. Resultados obtenidos para la metodología RAD-OPUS con el calculador hidráulico SparseSolver
Los resultados para diseños discretos, con el calculador hidráulico SparseSolver resultaron ser
notablemente peores en cuanto costo. Sin embargo, el número de iteraciones y el costo del diseño
continuo resultó ser muy parecido a los resultados del calculador hidráulico Epanet. Estos
resultados pueden verse en la Tabla 9 y Tabla 10, para SparseSolver y Epanet respectivamente.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
71
SPARSE SOLVER
Nombre
Tipo
Diseño
Flecha
Costo
Presión
mínima
(m)
No.
Iteraciones
Hanoi
HW(130)-PP-DOC(normal)
Continuo
0.1355
$ 5,412,941.43
27.45
0
HW(130)-PP-DOC(normal)-RP(2.6)+AD(5)+DD
Discreto
0.1355
$ 5,549,389.59
30.79
61
Balerma
DW-PP-DOC(normal)
Continuo
0.0483
$ 1,965,330.12
17.03
0
DW-PP-DOC(normal)-RP(2.6)+AD(1)+DD
Discreto
0.0483
$ 2,089,194.10
20
1301
R28
DW-PP-DOC(normal)
Continuo
0.0815
$ 145,805.25
14.97
0
DW-PP-DOC(normal)-RP(2.6)+AD(2)+DD
Discreto
0.0815
$ 153,478.63
15.02
95
Taichung
HW(100)-PP-DOC(normal)
Continuo
0.1007
$ 7,925,851.76
15.00
0
HW(100)-PP-DOC(normal)-RP(2.6)+AD(1)+DD
Discreto
0.1007
$ 9,005,132.37
15.48
50
Tabla 9. Resultados obtenidos para la metodología RAD-OPUS con el calculador hidráulico SparseSolver.
En los Numerales del 4.1 al 4.4 se mostraron los mejores resultados obtenidos con ela
metodología propuesta, para cada uno de los escenarios analizados (2,3 y 4 facotres) y para cada
una de las redes. Sin embargo no es posible inferir que calculador hidráulico provienen dichos
resultados; por lo tanto, se resumieron las pruebas de cada calculador hidráulico en las Tablas 11 y
12, para SparseSolver y Epanet respectivamente.
Las Tablas 11 y 12 muestran que para diseños discretos con la metodología Greedy Algorithm, con
el calculador hidráulico SparseSolver los resultados son notablemente peores en cuanto costo y
número de iteraciones. Para todos los escenarios y para todas las redes los resultados en costos
son más favorables para el calculador hidráulico Epanet.
Cabe destacar un patrón muy importante en el mínimo costo para cada red, mientras que para el
calculador Sparse Solver el mínimo costo para las redes Hanoi, R28 y Taichung, se encuentra en los
escenarios 3 factores, 4 factores y 2 factores respectivamente, para el calculador hidráulico Epanet
los mínimos se encontraron en el escenario de 3 factores para todas las redes lo cual se considera
una conclusión muy importante acerca del algoritmo.
EPANET
Nombre
Tipo
Diseño
Flecha
Costo
Presión
mínima
(m)
No.
Iteraciones
Hanoi
DW-PP-DOC(normal)
Continuo
0.1355
$ 5,412,941.43
27.81
0
HW(130)-PP-DOC(normal)-RP(2.6)+AD(5)+DD
Discreto
0.1355
$ 5,540,105.77
30.06
54
Balerma
DW-PP-DOC(normal)
Continuo
0.0483
$ 1,965,330.12
17.03
0
DW-PP-DOC(normal)-RP(2.6)+AD(1)+DD
Discreto
0.0483
$ 2,104,182.92
20
948
R28
DW-PP-DOC(normal)
Continuo
0.0815
$ 145,805.25
15.11
0
DW-PP-DOC(normal)-RP(2.6)+AD(1)+DD
Discreto
0.0815
$ 149,833.20
15.09
77
Taichung
HW(100)-PP-DOC(normal)
Continuo
0.1007
$ 7,925,851.76
15.00
0
HW(100)-PP-DOC(normal)-RP(2.6)+AD(2)+DD
Discreto
0.1007
$ 8,936,121.79
15.45
53
Tabla 10. Resultados obtenidos para la metodología RAD-OPUS con el calculador hidráulico Epanet.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
72
SPARSE SOLVER
Diametros
continuos
Diámetros
discretos
Algoritmo Voraz 2
Factores
Diámetros
discretos
Algoritmo Voraz 3
Factores
Diámetros
discretos
Algoritmo Voraz 4
Factores
Diámetros
discretos RAD
OPUS
Mejora
OPUS
Hanoi
Costo
$ 5,412,941.43 $ 5,580,247.40 $ 5,580,225.85 $ 5,611,953.67 $ 5,549,389.59 -0.56%
Iteraciones
0
708
1186
1197
61
Balerma
Costo
$ 1,965,330.12
N/A
N/A
N/A $ 2,089,194.10
N/A
Iteraciones
0
N/A
N/A
N/A
1301
R28
Costo
$ 145,805.25 $ 151,003.87 $ 150,565.74 $ 150,398.18 $ 153,478.63
2.01%
Iteraciones
0
4726
4749
4714
95
Taichung
Costo
$ 7,925,851.76 $ 8,980,288.50 $ 8,989,551.50 $ 9,060,276.76 $ 9,005,132.37
0.28%
Iteraciones
0
2005
2142
1862
50
Tabla 11. Resultados obtenidos para la metodología Greedy Algorithm con el calculador hidráulico SparseSolver.
Cabe anotar que existe una limitación de capacidad de memoria del calculador Sparse Solver, pues
este utiliza la memoria con la que se ejecuta el programa REDES, al estar programado en lenguaje
Delphi
10
bajo el compilador Delphi 6, la aplicación tiene un límite de uso de memoria lo cual se
traduce bajos velocidades de cálculo y desbordamiento de memoria señalizado por el programa
como “Out of memory”. Por lo anterior, cabe reiterar que no se hicieron pruebas para la red
Balerma con el calculador hidráulico SparseSolver y tampoco se hicieron pruebas de dos factores
de la red con el calculador hidráulico Epanet debido a que el tiempo de simulación es muy elevado
y las demás pruebas realizadas para las demás redes demostraron que los mejores resultados del
algoritmo se encontrarían al combinar tres factores y no dos ni cuatro. Por otro lado, en la Tablas
11 y 12 se evidencia que para todas las redes es mejor utilizar el calculador hidráulico Epanet.
10
Delphi es un entorno de desarrollo de software diseñado para la programación de propósito general con énfasis en la programación
visual. En Delphi se utiliza como lenguaje de programación de una versión moderna de Pascal llamada
Object Pascal
.
EPANET
Diametros
continuos
Diámetros
discretos
Algoritmo Voraz 2
Factores
Diámetros
discretos
Algoritmo Voraz 3
Factores
Diámetros
discretos
Algoritmo Voraz 4
Factores
Diámetros
discretos RAD
OPUS
Mejora
OPUS
Hanoi
Costo
$ 5,412,941.43 $ 5,580,247.40 $ 5,580,225.85 $ 5,600,890.84 $ 5,540,105.77 -0.01%
Iteraciones
0
30
28
28
54
Balerma
Costo
$ 1,965,330.12
N/A $ 2,076,309.19 $ 2,076,064.20 $ 2,104,182.92
1.34%
Iteraciones
0
N/A
153
155
948
R28
Costo
$ 145,805.25 $ 150,516.21 $ 149,262.81 $ 149,586.65 $ 149,833.20
0.38%
Iteraciones
0
38
41
37
77
Taichung
Costo
$ 7,925,851.76 $ 8,857,289.70 $ 8,813,021.79 $ 8,922,582.24 $ 8,936,121.79
1.38%
Iteraciones
0
15
18
21
53
Tabla 12. Resultados obtenidos para la metodología Greedy Algorithm con el calculador hidráulico Epanet.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
73
Ya habiendo concluido que la mejor estrategia es combinar tres factores y hacer siempre uso del
calculador hidráulico Epanet, se busco una relación entre los factores más significativos para
encontrar los mejores resultados con la metodología propuesta.
La anterior conclusión sobre el uso de tres factores se evidencian en las Tablas 13 y 14 que
resumen los pesos de la combinación factores que dieron como resultado el mejor diseño (Los
mejores diseños para cada red tiene fondo gris y pueden ser visualizados en las Tablas 11 y 12).
SPARSE SOLVER
Diámetros discretos
Algoritmo Voraz 2
Factores
Diámetros discretos
Algoritmo Voraz 3
Factores
Diámetros discretos Algoritmo
Voraz 4 Factores
Hanoi
Costo
IR
Costo Presión
IR
Costo Presión
IR
PuTI
0.6
0.4
0.4
0.4
0.2
0.4
0.2
0.2
0.2
R28
Costo
Presión
Costo Presión PuTI
Costo Presión
IR
PuTI
0.4
0.6
0.4
0.4
0.2
0.2
0.4
0.2
0.2
Taichung
Costo
Presión
Costo Presión
PuTI
Costo Presión
IR
PuTI
0.6
0.4
0.2
0.2
0.6
0.2
0.2
0.2
0.4
Tabla 13. Peso de los ponderadores para los mejores resultados obtenidos para la metodología Greedy Algorithm con el calculador
hidráulico SparseSolver.
EPANET
Diámetros discretos
Algoritmo Voraz 2
Factores
Diámetros discretos
Algoritmo Voraz 3
Factores
Diámetros discretos Algoritmo
Voraz 4 Factores
Hanoi
Costo
IR
Costo Presión
IR
Costo Presión
IR
PuTI
0.6
0.4
0.4
0.4
0.2
0.4
0.2
0.2
0.2
Balerma
Costo Presión
IR
Costo Presión
IR
PuTI
0.4
0.2
0.4
0.4
0.2
0.2
0.2
R28
Costo
Presión
Costo Presión PuTI
Costo Presión
IR
PuTI
0.4
0.6
0.4
0.4
0.2
0.2
0.4
0.2
0.2
Taichung
Presión
PuTI
Presión PuTI
IR
Costo Presión
IR
PuTI
0.4
0.6
0.4
0.2
0.4
0.2
0.4
0.2
0.2
Tabla 14. Peso de los ponderadores para los mejores resultados obtenidos para la metodología Greedy Algorithm con el calculador
hidráulico Epanet.
Al analizar sobre todo la Tabla 13 por las consideraciones anteriormente plantadas, se encuentra
que para todos los casos de mejor diseño la presión tiene un peso considerable de 0.4 (para un
caso de 0.2), así mismo para tres de los cuatro redes el costo tiene un peso significativo en la
ecuación de elección de la tubería, un peso de 0.4 para la mayoría de casos (de 0.2 para el caso de

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
74
la Red R28). Otra conclusión muy importante es que a pesar de lo expuesto anteriormente,
considerar una combinación única de los factores costo y presión no se traduce en mejores diseño;
de hecho en solo un caso de tres redes probadas con este escenario resultó esta combinación.
Cabe destacar, que contrario a la lógica, hacer menos vulnerable la red respecto a la original es
importante, pues en 3 redes dicho parámetro pesó dentro de la Ecuación 15. Así mismo en
algunos casos la potencia unitaria también hizo parte de la ecuación con un peso máximo de 0.2.
Estas conclusiones derivan en los resultados del escenario de 4 parámetros, donde para todas las
redes los parámetros PUTi e IR tiene un peso de 0.2 y el costo y la presión intercalan valores de 0.4
y 0.2 lo que abre la posible a diseño aún mejores asignando valores de 0.3 para estos dos últimos
parámetros.
Así mismo, se abre la posibilidad a mejores diseño con el escenario de 3 factores, haciendo
cambios en los pesos de cada parámetro en pasos de 0.1 o de 0.001. Sin embargo, el propósito de
este estudio es dar cuenta del rango de valores que deberían tener los pesos de cada parámetro;
dicha conclusión se muestra a continuación en la Tabla 14.
Mc
Mp
Mir
Mpu
0.2-0.4
0.2-0.4
0.2 - 0.4
0 - 0.2
Tabla 15. Rango de valores para los parámetros ponderadores de la regla de decisión.
Estos resultados o patrones encontrados corroboran la universalidad de la metodología y
permiten afirmar que la metodología Greedy Algorithm con OPUS como inicio en caliente es
supremamente eficiente y eficaz al encontrar diseños de RDAP cercanos al óptimo.
Además, se puede observar que la ventaja de esta metodología es más notoria en redes grandes,
como Balerma, en las cuales los algoritmos metaheurísticos, que tienen un componente aleatorio
importante, requieren de millones de simulaciones para explorar el espacio de búsqueda y llegar a
diseños cercanos al óptimo. En contraste, la metodología Greedy Algorithm combina la
comprensión hidráulica del sistema con el elemento estocástico que reduce el número de
iteraciones.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
75
5. CONCLUSIONES
En este trabajo de investigación se desarrolló, implementó y probó con éxito una metodología
heurística para el diseño optimizado de redes de distribución de agua potable (RDAP) que se basa
en el resultado de la metodología OPUS, la cual es netamente de comprensión de la hidráulica y la
topología del sistema; adicionalmente, esta heurística involucre factores hidráulicos que
demostraron ser significativos para hallar el Óptimo, esto a diferencia de la mayoría de
metodologías de diseño existentes, las cuales se fundamentan en una búsqueda exhaustiva de un
amplio espacio de solución sin tener en cuenta consideraciones hidráulicas las cuales mostraron
repercutir sustancialmente en el número de iteraciones y la reducción de la función objetivo.
Mediante este trabajo se comprobó que es posible mejor un diseño continuo de mínimo costo de
una RDAP a pesar de ser redondeado, si se utiliza dicha solución como un Hot Start que reduce
significativamente el espacio de solución y asegura estar muy cerca del óptimo global. En esta
investigación se estudió en detalle la variación en la función objetivo de costo en función de la
importancia que se le daba a las características analizadas en la regla de decisión ponderada que
es el punto crítico de la metodología a propuesta; y finalmente se establecieron unos valores
óptimos en los pesos de dichas características que aseguren encontrar el óptimo con esta
metodología para cualquier red de distribución. Con base en la metodología OPUS se obtiene una
pre-configuración de la red que cumple con las restricciones hidráulicas del problema del diseño
de RDAP, pero no con las restricciones comerciales, dado que los diámetros de las tuberías de esta
pre-configuración son continuos. Para redondear dichos diámetros a valores discretos contenidos
dentro del conjunto de diámetros comerciales disponibles, se implementó un procedimiento
algorítmico de baja complejidad, que asegura mantener la proporcionalidad de la red, generar el
mejor espacio de búsqueda para la heurística y requiere un número pequeño de simulaciones
hidráulicas, lo cual constituye una gran ventaja para la metodología planteada. Finalmente, para la
optimización de la solución redondeada se aplicó una heurística que combina nociones hidráulicas
con el elemento estocástico de este tipo de procedimientos.
La metodología desarrollada fue aplicada a tres redes de prueba ampliamente reportadas en la
literatura: Hanoi, Taichung y Balerma y una red hipotética adicional, la red R28 creada por el
CIAUCA. Para estas redes se encontraron diseños óptimos o muy cercanos al óptimo en un
número muy pequeño de simulaciones hidráulicas en comparación con el número simulaciones
requeridas por los algoritmos metaheurísticos reportados en la literatura. Con base en estos
resultados se puede afirmar que la metodología propuesta es eficaz y eficiente para encontrar
diseños óptimos de RDAP.
La baja complejidad y la eficiencia de la metodología OPUS constituyen una gran ventaja
especialmente en el caso de RDAP grandes, en las cuales los algoritmos metaheurísticos, que
tienen un componente aleatorio importante, requieren de millones de simulaciones para explorar
el espacio de búsqueda y llegar a diseños cercanos al óptimo. Al combinar esta herramienta con la

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
76
metodología en este estudio planteada se cuenta con procedimiento determinístico, lo que la hace
diferente a otras metodologías netamente heurísticas, donde sus resultados obtenidos al correr
estos algoritmos son siempre diferentes, por lo que se deben realizar cientos de corridas (en cada
una de las cuales se realizan miles de simulaciones hidráulicas) hasta obtener un buen resultado,
que es el que finalmente reportan los autores en las publicaciones.
Contrario a estos algoritmos, la metodología OPUS-Greedy Algorithm mostró no tener
componentes aleatorios significativos al mantener el peso de los ponderadores en los rangos
aconsejados: al aplicarla dentro de dichos rangos siempre se obtienen soluciones mejores que las
soluciones que arroja la metodología OPUS-RAD presente en REDES 2013, como se demostró en
las pruebas realizadas con las redes de Hanoi, R28, Taicung y Balerma, se acerca siempre al diseño
de mínimo costo. Adicional a lo anterior, la metodología OPUS-Greedy Algorithm permite
comprender la magnitud del efecto de los factores: costo, presión, PUTi y el Indice de Resiliencia,
en los diseños óptimos, lo cual podría convertirse en una herramienta útil para investigaciones
futuras sobre la optimización de redes existentes.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
77
6. RECOMENDACIONES
A partir de la investigación desarrollada y de los resultados obtenidos en esta, se sugiere realizar
las siguientes actividades para complementar y mejorar la metodología que combina el uso de
OPUS para el diseño óptimo de RDAP propuesta:
-
Probar la metodología de OPUS-Greedy Algortihm en redes reales complejas: las pruebas
realizadas y presentadas en este trabajo corresponden a redes hipotéticas (e.g. redes de
Hanoi y R28) o con características topológicas e hidráulicas anómalas (e.g. red de Balerma,
que corresponde a un distrito de riego y no a una red de distribución normal); por lo tanto,
sería interesante analizar el desempeño de la metodología propuesta en redes reales con
diferentes características topográficas, topológicas e hidráulicas.
-
Revisar y mejorar el procedimiento que cuenta las el número iteraciones o simulaciones
hidráulicas para el caso del calculador hidráulico Epanet pues los resultados presentan
unos valores que podrían indicar que no está teniendo en cuenta todas las corridas
hidráulicas de la metodología propuesta. Se hace énfasis en el calculador Epanet pues en
los resultados mostrados para el calculador SparseSolver se observa el esperado
crecimiento significativo del número de simulaciones.
-
Incluir dentro de la regla de decisión ponderada otros factores tales como: pérdidas
totales, longitud, cociente de estas dos variables y delta de dichos cocientes. Debido a que
estos mostraron ser las mejores opciones para la elección de la tubería a aumentar en la
metodología de OPUS-RAD.
-
Estudiar la implementación de de otros algoritmos de redondeo para aumentar o reducir
reducción en el espacio de búsqueda y evaluar el efecto de dicho cambio en el espacio al
evaluar la metodología propuesta de tomar como “semilla” el diseño obtenido con la
metodología OPUS.
-
Hacer más pruebas de escenario de 3 factores con pequeñas variaciones de los pesos (0.1
a 0.01) dentro de los rangos establecidos en este estudio para pulir aun más dichos rangos
y definir en lo posible unos valores fijos en los ponderadores que arrojen una solución
buena para cualquier red.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
78
7. REFERENCIAS
Cunha, D., and Sousa, J. (1999). “Water distribution network design optimization: simulated
annealing approach.” J. Water Resour. Plann. Manage., 125(4), 215–221.
Cunha, M. y Ribeiro, L., 2004. Tabu search algorithms for water network optimization. European
Journal of Operational Research, 157 (3), 746 - 758.
Dandy, G., Simpson, A., and Murphy, L. (1996). “An improved genetic algorithm for pipe network
optimization.” Water Resour. Res., 32(2), 449–458.
Decreto 475 (Normas Técnicas de Calidad del Agua Potable 1998) de marzo 10 de 1998, expedido
por el Ministerio de Salud Pública de la República de Colombia.
Elbeltagi, E., Hegazy, T., and Grierson, D. (2005). “Comparison among five evolutionary-based
optimization algorithms.” Adv. Eng. Inf., 19(1), 43–53.
Eusuff, M., and Lansey, K. (2003). “Optimization of water distribution network design using the
shuffled frog leaping algorithm.” J. Water Resour. Plann. Manage., 129(3), 210–225.
Geem, Z. (2006). “Optimal cost design of water distribution networks using harmony search.” Eng.
Optim., 38(3), 259–277.
Goldberg, D.E. y Kuo, C.H., 1987. Genetic algorithm in pipeline optimization. Journal of Computing
in Civil Engineering, 1 (2), 128–141.
Holland, J. (1992). Adaptation in natural and artificial systems: An introductory analysis with
applications to biology, control, and artificial intelligence, MIT Press, Cambridge, MA.
Kadu, S.M., Gupta, R. y Bhave, P.R., 2008. Optimal design of water networks using a modified
genetic algorithm with reduction in search space. Journal of Water Resources Planning and
Management, 134 (2), 147 - 160.
Kang, D., and Lansey, K. (2012). “Revisiting optimal water distribution system design: Issues and a
heuristic hierarchical approach.” J. Water Resour. Plann. Manage., 138(3), 208–217.
Keedwell, E., and Khu, S. (2005). “A hybrid genetic algorithm for the design of water distribution
networks.” Eng. Appl. Artif. Intell., 18(4), 461–472.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
79
Maier, H., et al. (2003). “Ant colony optimization for design of water distribution systems.” J.
Water Resour. Plann. Manage., 129(3), 200–209.
Manuel A. Andrade; Doosun Kang; Christopher Y. Choi; and Kevin Lansey, M.ASCE (2013)
“Heuristic Postoptimization Approaches for Design of Water Distribution Systems” Journal of
water resources planning and management © asce / july/august 2013 / 387 - 395
Reca, J. y Martinez, J., 2006. Genetic algorithms for the design of looped irrigation water
distribution networks. Water Resources Research, 44, W05416.
Reca, J., Martinez, J., Gil, C. y Baños, R., 2007. Application of several meta-heuristic techniques to
the optimization of real looped water distribution networks. Water Resources Management,
22, 1367 - 1379.
Saldarriaga, Juan G, 2007. Hidráulica de Tuberías: abastecimiento de agua, redes, riegos. Editorial
Alfaomega. Bogotá, Colombia. ISBN/ISSN: 978-958-682-680-8
Saldarriaga, J. Páez, D, León, N, López, L and Cuero, P. (2013). Historical development of power use
methods for WDS design and their evolution towards optimization metaheuristics.
Savic, D.A. y Walters, G.A., 1997. Genetic algorithms for least cost design of water distribution
networks.
Journal of Water Resources Planning and Management, 123 (2), 67 – 77.
Simpson, A., Dandy, G., and Murphy, L. (1994). “Genetic algorithms compared to other techniques
for pipe optimization.” J. Water Resour. Plann. Manage., 120(4), 423–443.
Takahashi, S., Saldarriaga, S., Hernández, F., Díaz, D. and Ochoa, S., 2010. An energy methodology
for the design of water distribution systems. In Proceedings of the World Environmental and
Water Resources Congress 2010, ASCE.
Templeman, A. (1982). “Discussion of ‘Optimization of looped water distribution systems’.” J.
Environ. Eng. Div., 108(3), 599–602.
Tospornsampan, J., Kita, I., Ishii, M. y Kitamura, Y., 2007a. Split-pipe design of water distribution
network using simulated annealing. International Journal of Computer, Information, and
Systems Science, and Engineering, 1 (3), 153 - 163.
Vairavamoorthy, K. y Ali, M., 2005. Pipe index vector: A method to improve genetic-algorithm-
based pipe optimization. Journal of Hydraulic Engineering, 131 (12), 1117 - 1125.
Villalba, G., 2004. Algoritmos de optimización combinatoria aplicados al diseño de redes de
distribución de agua potable. Tesis (Magíster). Universidad de los Andes, Bogotá, Colombia.
Walski, T., Chase, D., Savic, D., Grayman,W., Beckwith, S., and Koelle, E. (2003). Advanced water
distribution modeling and management, Haestad, Waterbury, CT.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
80
Wu, Z., and Simpson, A. (2001). “Competent genetic-evolutionary optimization of water
distribution systems.” J. Comput. Civ. Eng., 15(2), 89–101.
Yates, D., Templeman, A., and Boffey, T. (1984). “The computational complexity of the problem of
determining least capital cost designs for water supply networks.” Eng. Optim., 7(2), 143–155.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
81
ANEXOS
SPARSE SOLVER
COSTO-PRESIÓN
COSTO-PUTI
Mc Mp
Presión
mínima
(m)
No.
Iteraciones
Costo
Mc
Mputi
Presión
mínima
(m)
No.
Iteraciones
Costo
Hanoi
0
1
30.64
1262
$ 5,661,181.87
0
1
30.49
1166
$ 5,765,197.26
0.2 0.8
30.64
1289
$ 5,661,181.87
0.2
0.8
30.29
1139
$ 5,787,090.90
0.4 0.6
30.64
1050
$ 5,613,135.54
0.4
0.6
31.56
1156
$ 5,611,953.67
0.6 0.4
30.34
515
$ 5,730,512.53
0.6
0.4
30.35
708
$ 5,580,247.40
0.8 0.2
30.34
514
$ 5,730,512.53
0.8
0.2
30.34
513
$ 5,730,512.53
1
0
30.34
503
$ 5,730,512.53
1
0
30.34
503
$ 5,730,512.53
R28
0
1
16.200
4645
$ 153,996.80
0
1
15.020
4321
$ 157,440.59
0.2 0.8
15.190
4736
$ 152,448.50
0.2
0.8
15.290
4448
$ 154,233.57
0.4 0.6
15.030
4726
$ 151,003.87
0.4
0.6
15.020
3782
$ 153,469.91
0.6 0.4
15.030
2079
$ 156,942.90
0.6
0.4
15.010
2662
$ 157,534.60
0.8 0.2
15.000
1386
$ 165,568.80
0.8
0.2
15.000
1360
$ 165,568.80
1
0
15.000
1360
$ 165,568.80
1
0
15.000
1360
$ 165,568.80
Taichung
0
1
15.15
2194
$ 9,040,221.34
0
1
15.18
1978
$ 9,040,927.48
0.2 0.8
15.38
2185
$ 9,019,062.10
0.2
0.8
15.07
2061
$ 9,233,294.57
0.4 0.6
15.18
1823
$ 9,236,842.77
0.4
0.6
15.06
1855
$ 9,126,107.74
0.6 0.4
15.04
995
$ 10,345,537.86
0.6
0.4
15.04
1016
$ 10,276,933.90
0.8 0.2
15.04
961
$ 10,345,537.86
0.8
0.2
15.04
936
$ 10,348,626.89
1
0
15.04
893
$ 10,345,537.86
1
0
15.04
893
$ 10,345,537.86
Coeficiente
in
mm
exponente
Pmin
m.c.a
Flecha
HW
Hanoi
1.1
0.008592947
1.5
30
0.1355
130
Balerma
0.00041245
2.0618
20
0.1848
R28
N/A
0.015
1.45
15
0.0815
Taichung
1.9482
1.2571
15
0.1007
100
Tabla 16. Valores ingresados como parámetros al programa REDES 2013.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
82
COSTO-INDICE RESILIENCIA
PRESIÓN-PUTI
Mc Mir
Presión
mínima
(m)
No.
Iteraciones
Costo
Mp
Mputi
Presión
mínima
(m)
No.
Iteraciones
Costo
Hanoi
0
1
30.389
743
$ 5,995,669.33
0
1
30.49
1166
$ 5,765,197.26
0.2 0.8
30.331
983
$ 5,834,807.50
0.2
0.8
30.44
1175
$ 5,792,255.48
0.4 0.6
30.6
1168
$ 5,608,483.20
0.4
0.6
30.09
1224
$ 5,652,801.56
0.6 0.4
30.351
708
$ 5,580,247.40
0.6
0.4
30.64
1237
$ 5,661,181.87
0.8 0.2
30.34
513
$ 5,730,512.53
0.8
0.2
30.64
1245
$ 5,661,181.87
1
0
30.34
503
$ 5,730,512.53
1
0
30.64
1262
$ 5,661,181.87
R28
0
1
15.01
2335
$ 165,496.63
0
1
15.020
4321
$ 157,440.59
0.2 0.8
15.08
3417
$ 155,158.67
0.2
0.8
15.28
4616
$ 153,817.10
0.4 0.6
15
2699
$ 158,432.30
0.4
0.6
15.85
4617
$ 153,493.75
0.6 0.4
15
2840
$ 156,789.63
0.6
0.4
15.18
4710
$ 151,512.80
0.8 0.2
15
1333
$ 165,568.80
0.8
0.2
16.2
4645
$ 153,996.80
1
0
15.000
1360
$ 165,568.80
1
0
16.200
4645
$ 153,996.80
Taichung
0
1
15.01
1258
$ 10,375,436.23
0
1
15.18
1978
$ 9,040,927.48
0.2 0.8
15.06
1782
$ 9,211,138.97
0.2
0.8
15.75
2142
$ 9,050,280.78
0.4 0.6
15.03
1725
$ 9,235,290.20
0.4
0.6
15.85
2174
$ 9,057,986.97
0.6 0.4
15.04
1010
$ 10,276,993.90
0.6
0.4
15.15
2193
$ 9,040,211.34
0.8 0.2
15.02
1107
$ 9,998,013.73
0.8
0.2
15.15
2199
$ 9,040,221.34
1
0
15.04
893
$ 10,345,537.86
1
0
15.15
2194
$ 9,040,221.34
PRESIÓN-INDICE RESILIENCIA
PUTI-INDICE RESILIENCIA
Mp Mir
Presión
mínima
(m)
No.
Iteraciones
Costo
Mputi
Mir
Presión
mínima
(m)
No.
Iteraciones
Costo
Hanoi
0
1
30.38
743
$ 5,995,669.33
0
1
30.38
743
$ 5,995,669.33
0.2 0.8
30.09
1142
$ 5,794,651.30
0.2
0.8
30.39
74
$ 5,995,669.33
0.4 0.6
31.238
1215
$ 5,778,105.72
0.4
0.6
30.17
869
$ 5,895,375.87
0.6 0.4
31.23
1219
$ 5,778,105.72
0.6
0.4
30.16
999
$ 5,880,775.50
0.8 0.2
31.238
1230
$ 5,778,105.72
0.8
0.2
30.09
1131
$ 5,794,651.30
1
0
30.64
1262
$ 5,661,181.87
1
0
30.49
1166
$ 5,765,197.26
R28
0
1
15.02
4321
$ 157,440.59
0
1
15.01
2335
$ 165,496.63
0.2 0.8
15.28
4616
$ 153,817.10
0.2
0.8
15
2589
$ 162,667.53
0.4 0.6
15.85
4617
$ 153,493.75
0.4
0.6
15
2805
$ 161,403.84
0.6 0.4
15.18
4710
$ 151,512.80
0.6
0.4
15
2905
$ 166,381.36
0.8 0.2
16.2
4645
$ 153,996.80
0.8
0.2
15
3986
$ 161,860.57
1
0
16.200
4645
$ 153,996.80
1
0
15.020
4321
$ 157,440.59
Taichung
0
1
15.01
1258
$ 10,375,436.23
0
1
15.01
1258
$ 10,375,436.23
0.2 0.8
15.03
1823
$ 9,216,097.68
0.2
0.8
15.01
1258
$ 10,375,436.23
0.4 0.6
15.04
2005
$ 8,980,288.50
0.4
0.6
15.04
1748
$ 9,201,941.62
0.6 0.4
15.62
2116
$ 9,039,915.80
0.6
0.4
15.05
1579
$ 9,429,109.24
0.8 0.2
15.76
2189
$ 8,995,976.30
0.8
0.2
15.24
1957
$ 9,141,835.30
1
0
15.15
2194
$ 9,040,221.34
1
0
15.18
1978
$ 9,040,927.48
Tabla 17. Prueba del escenario de dos factores para el calculador SparseSolver.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
83
EPANET
COSTO-PRESIÓN
COSTO-PUTI
Mc Mp
Presión
mínima
(m)
No.
Iteraciones
Costo
Mc
Mputi
Presión
mínima
(m)
No.
Iteraciones
Costo
Hanoi
0
1
30.98
28
$ 5,661,181.87
0
1
30.83
26
$ 5,765,197.26
0.2 0.8
30.98
28
$ 5,661,181.87
0.2
0.8
30.34
27
$ 5,736,632.53
0.4 0.6
31.63
30
$ 5,637,824.87
0.4
0.6
30.03
27
$ 5,731,467.15
0.6 0.4
30.68
30
$ 5,730,512.53
0.6
0.4
30.69
30
$ 5,580,247.40
0.8 0.2
30.68
30
$ 5,730,512.53
0.8
0.2
30.68
30
$ 5,730,512.53
1
0
30.68
30
$ 5,730,512.53
1
0
30.68
30
$ 5,730,512.53
R28
0
1
15.060
37
$ 152,362.42
0
1
15.120
34
$ 154,751.10
0.2 0.8
15.340
36
$ 152,448.50
0.2
0.8
15.390
36
$ 151,457.57
0.4 0.6
14.970
38
$ 150,516.21
0.4
0.6
14.990
55
$ 157,453.90
0.6 0.4
14.990
55
$ 155,465.92
0.6
0.4
15.000
57
$ 156,744.13
0.8 0.2
15.000
62
$ 163,055.30
0.8
0.2
15.000
62
$ 163,980.48
1
0
15.000
62
$ 163,980.48
1
0
15.000
62
$ 163,980.48
Taichung
0
1
16.68
18
$ 9,067,160.23
0
1
15.33
17
$ 9,079,274.41
0.2 0.8
15.66
18
$ 9,024,841.74
0.2
0.8
15.22
18
$ 9,238,624.17
0.4 0.6
15.09
23
$ 9,109,887.29
0.4
0.6
15.38
17
$ 8,914,577.24
0.6 0.4
15.01
26
$ 10,059,672.43
0.6
0.4
15.01
26
$ 10,294,383.47
0.8 0.2
15.01
26
$ 10,059,672.43
0.8
0.2
15.01
26
$ 10,294,383.47
1
0
15.09
33
$ 10,496,375.98
1
0
15.09
33
$ 10,496,375.98
COSTO-INDICE RESILIENCIA
PRESIÓN-PUTI
Mc Mir
Presión
mínima
(m)
No.
Iteraciones
Costo
Mp
Mputi
Presión
mínima
(m)
No.
Iteraciones
Costo
Hanoi
0
1
0
1
30.49
27
$ 5,765,197.26
0.2 0.8
30.7
29
$ 5,836,040.74
0.2
0.8
30.44
27
$ 5,792,255.48
0.4 0.6
30.27
29
$ 5,671,242.90
0.4
0.6
30.09
27
$ 5,652,801.56
0.6 0.4
30.69
30
$ 5,580,247.40
0.6
0.4
30.64
27
$ 5,661,181.87
0.8 0.2
30.68
30
$ 5,730,512.53
0.8
0.2
30.64
27
$ 5,661,181.87
1
0
30.68
30
$ 5,730,512.53
1
0
30.64
28
$ 5,661,181.87
R28
0
1
14.99
54
$ 164,056.20
0
1
15.12
34
$ 154,751.10
0.2 0.8
15
59
$ 159,895.23
0.2
0.8
15.44
34
$ 153,695.18
0.4 0.6
15
56
$ 157,036.40
0.4
0.6
15.04
36
$ 152,690.70
0.6 0.4
15
58
$ 156,872.72
0.6
0.4
15.19
37
$ 152,777.50
0.8 0.2
15
62
$ 163,980.48
0.8
0.2
15.19
37
$ 152,777.50
1
0
15
62
$ 163,980.48
1
0
15.06
37
$ 152,362.42

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
84
Taichung
0
1
15
19
$ 9,505,126.32
0
1
15.33
17
$ 9,079,274.41
0.2 0.8
15.26
21
$ 9,211,138.97
0.2
0.8
15.41
17
$ 9,006,920.42
0.4 0.6
15.09
23
$ 9,375,636.95
0.4
0.6
15.03
15
$ 8,857,289.70
0.6 0.4
15
26
$ 10,051,915.60
0.6
0.4
16.25
18
$ 8,986,417.73
0.8 0.2
15.01
27
$ 10,219,346.44
0.8
0.2
15.34
19
$ 9,040,221.34
1
0
15.09
33
$ 10,496,375.98
1
0
16.68
18
$ 9,067,160.23
PRESIÓN-INDICE RESILIENCIA
PUTI-INDICE RESILIENCIA
Mp Mir
Presión
mínima
(m)
No.
Iteraciones
Costo
Mputi
Mir
Presión
mínima
(m)
No.
Iteraciones
Costo
Hanoi
0
1
30.38
27
$ 5,995,669.33
0
1
30.38
28
$ 5,995,669.33
0.2 0.8
30.09
27
$ 5,794,651.30
0.2
0.8
30.39
28
$ 5,995,669.33
0.4 0.6
31.24
27
$ 5,778,105.72
0.4
0.6
30.17
27
$ 5,895,375.87
0.6 0.4
31.23
27
$ 5,778,105.72
0.6
0.4
30.16
27
$ 5,880,775.50
0.8 0.2
31.24
27
$ 5,778,105.72
0.8
0.2
30.09
27
$ 5,794,651.30
1
0
30.64
28
$ 5,661,181.87
1
0
30.49
26
$ 5,765,197.26
R28
0
1
14.99
54
$ 164,056.20
0
1
14.99
54
$ 164,056.20
0.2 0.8
15
39
$ 154,151.88
0.2
0.8
0.4 0.6
15
40
$ 151,425.93
0.4
0.6
15.09
39
$ 156,510.33
0.6 0.4
15.45
37
$ 152,371.31
0.6
0.4
15
36
$ 156,015.60
0.8 0.2
15.52
36
$ 151,630.62
0.8
0.2
15.12
34
$ 154,751.10
1
0
#####
37
$ 152,362.42
1
0
15.12
34
$ 154,751.10
Taichung
0
1
15
19
$ 9,505,126.32
0
1
15
19
$ 9,505,126.32
0.2 0.8
15.09
32
$ 9,123,754.50
0.2
0.8
15
23
$ 9,646,358.70
0.4 0.6
15.12
20
$ 8,916,810.76
0.4
0.6
15.01
25
$ 9,963,798.84
0.6 0.4
15.38
20
$ 8,968,731.14
0.6
0.4
15.01
17
$ 8,951,156.45
0.8 0.2
15.9
18
$ 8,995,976.30
0.8
0.2
15.05
15
$ 8,867,681.95
1
0
16.68
18
$ 9,067,160.23
1
0
15.33
17
$ 9,079,274.41
Tabla 18. Prueba del escenario de dos factores para el calculador Epanet.
SPARSE SOLVER
COSTO-PRESIÓN-PUTI
COSTO-PRESION-INDICE RESILIENCIA
Hanoi
Mc Mp Mpu
Presión
mínima
(m)
No.
Iteraciones
Costo
Mc Mpu Mir
Presión
mínima
(m)
No.
Iteraciones
Costo
0.2 0.6 0.2
30.59
1261
$ 5,705,652.17 0.2 0.6
0.2
30.28
1139
$ 5,787,090.90
0.2 0.4 0.4
30.59
1240
$ 5,705,652.17 0.2 0.4
0.4
30.21
965
$ 5,818,376.16
0.2 0.2 0.6
30.01
1244
$ 5,700,145.87 0.2 0.2
0.6 30.051
1150
$ 5,740,442.64
0.4 0.4 0.2
31.55
1186
$ 5,611,953.67 0.4 0.4
0.2
31.55
1157
$ 5,611,953.67
0.4 0.2 0.4
31.55
1193
$ 5,611,953.67 0.4 0.2
0.4
30.6
1165
$ 5,608,483.20
0.6 0.2 0.2
30.35
715
$ 5,580,247.40 0.6 0.2
0.2
30.53
708
$ 5,580,247.40
R-28
Mc Mp Mpu
Presión
mínima
(m)
No.
Iteraciones
Costo
Mc Mpu Mir
Presión
mínima
(m)
No.
Iteraciones
Costo
0.2 0.6 0.2
15.24
4770
$ 151,750.50 0.2 0.6
0.2
15.03
3398
$ 156,423.72

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
85
0.2 0.4 0.4
15.85
4757
$ 152,307.49 0.2 0.4
0.4
15
2968
$ 156,600.74
0.2 0.2 0.6
15.03
4861
$ 152,683.18 0.2 0.2
0.6
15.09
3307
$ 155,716.13
0.4 0.4 0.2
15.41
4749
$ 150,565.74 0.4 0.4
0.2
15
3423
$ 155,156.10
0.4 0.2 0.4
15.04
3857
$ 151,828.66 0.4 0.2
0.4
15.08
3203
$ 155,600.38
0.6 0.2 0.2
15.02
2708
$ 156,748.42 0.6 0.2
0.2
15.01
2690
$ 157,115.26
Taichung
Mc Mp Mpu
Presión
mínima
(m)
No.
Iteraciones
Costo
Mc Mpu Mir
Presión
mínima
(m)
No.
Iteraciones
Costo
0.2 0.6 0.2
15.38
2180
$ 9,019,062.10 0.2 0.6
0.2
15.17
1773
$ 9,146,233.60
0.2 0.4 0.4
15.38
2158
$ 9,019,062.10 0.2 0.4
0.4
15.19
1787
$ 9,153,826.19
0.2 0.2 0.6
15.3
2142
$ 8,989,551.50 0.2 0.2
0.6
15.09
1780
$ 9,217,303.93
0.4 0.4 0.2
15.76
1882
$ 9,194,179.33 0.4 0.4
0.2
15.64
1738
$ 9,379,970.76
0.4 0.2 0.4
15.76
1874
$ 9,194,179.33 0.4 0.2
0.4
15.15
1735
$ 9,235,290.20
0.6 0.2 0.2
15.02
1133
$ 9,998,013.73 0.6 0.2
0.2
15.01
1035
$ 10,208,185.58
COSTO-PUTI-RESILIENCIA
PRESIÓN-PUTI-INDICE RESILIENCIA
Hanoi
Mc Mp Mir
Presión
mínima
(m)
No.
Iteraciones
Costo
Mp Mpu Mir
Presión
mínima
(m)
No.
Iteraciones
Costo
0.2 0.6 0.2
31.98
1286
$ 5,745,571.90 0.2 0.6
0.2
30.48
1197
$ 5,765,197.26
0.2 0.4 0.4
30.59
1300
$ 5,705,652.17 0.2 0.4
0.4 30.489
1172
$ 5,765,197.26
0.2 0.2 0.6
30.59
1301
$ 5,705,652.17 0.2 0.2
0.6
30.29
1142
$ 5,863,975.33
0.4 0.4 0.2
30.88
1186
$ 5,580,225.85 0.4 0.4
0.2
31.23
1222
$ 5,778,105.72
0.4 0.2 0.4
31.55
1180
$ 5,611,953.67 0.4 0.2
0.4
31.23
1209
$ 5,778,105.72
0.6 0.2 0.2
30.35
715
$ 5,580,247.40 0.6 0.2
0.2
31.23
1213
$ 5,778,105.72
R-28
Mc Mp Mir
Presión
mínima
(m)
No.
Iteraciones
Costo
Mp Mpu Mir
Presión
mínima
(m)
No.
Iteraciones
Costo
0.2 0.6 0.2
15.65
4665
$ 152,100.10 0.2 0.6
0.2
15.58
4615
$ 154,538.98
0.2 0.4 0.4
15.14
3837
$ 153,382.68 0.2 0.4
0.4
15.24
4912
$ 151,248.17
0.2 0.2 0.6
15.05
3334
$ 155,236.61 0.2 0.2
0.6
15.01
3239
$ 158,060.32
0.4 0.4 0.2
15.04
3785
$ 151,357.47 0.4 0.4
0.2
15.04
4721
$ 151,371.49
0.4 0.2 0.4
15.01
3507
$ 153,657.82 0.4 0.2
0.4
15.36
4769
$ 151,421.23
0.6 0.2 0.2
15.06
2435
$ 158,762.48 0.6 0.2
0.2
15.11
4718
$ 151,544.55
Taichung
Mc Mp Mir
Presión
mínima
(m)
No.
Iteraciones
Costo
Mp Mpu Mir
Presión
mínima
(m)
No.
Iteraciones
Costo
0.2 0.6 0.2
15.44
2236
$ 9,011,113.26 0.2 0.6
0.2
15.17
1773
$ 9,176,233.60
0.2 0.4 0.4
15.11
1890
$ 9,177,977.24 0.2 0.4
0.4
15.19
1787
$ 9,153,826.19
0.2 0.2 0.6
15.73
1845
$ 9,215,009.37 0.2 0.2
0.6
15.09
1780
$ 9,217,303.93
0.4 0.4 0.2
15.76
1902
$ 9,194,179.33 0.4 0.4
0.2
15.64
1738
$ 9,379,970.76
0.4 0.2 0.4
15.09
1866
$ 9,173,365.30 0.4 0.2
0.4
15.15
1735
$ 9,235,290.20
0.6 0.2 0.2
15.02
1133
$ 9,998,013.73 0.6 0.2
0.2
15.01
1035
$ 10,208,185.58
Tabla 19. Prueba del escenario de tres factores para el calculador SparseSolver.

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
86
EPANET
COSTO-PRESIÓN-PUTI
COSTO-PRESION-INDICE RESILIENCIA
Hanoi
Mc Mp Mpu
Presión
mínima
(m)
No.
Iteraciones
Costo
Mc Mpu Mir
Presión
mínima
(m)
No.
Iteraciones
Costo
0.2 0.6 0.2
30.6
28
$ 5,705,652.17 0.2 0.6
0.2
30.3
28
$ 5,787,090.90
0.2 0.4 0.4
30.6
28
$ 5,705,652.17 0.2 0.4
0.4
30.2
28
$ 5,818,376.16
0.2 0.2 0.6
30
28
$ 5,700,145.87 0.2 0.2
0.6
30.1
28
$ 5,740,442.64
0.4 0.4 0.2
31.6
28
$ 5,611,953.67 0.4 0.4
0.2
31.6
28
$ 5,611,953.67
0.4 0.2 0.4
31.6
29
$ 5,611,953.67 0.4 0.2
0.4
30.6
29
$ 5,608,483.20
0.6 0.2 0.2
30.4
30
$ 5,580,247.40 0.6 0.2
0.2
30.5
30
$ 5,580,247.40
Balerma
Mc Mp Mpu
Presión
mínima
(m)
No.
Iteraciones
Costo
Mc Mpu Mir
Presión
mínima
(m)
No.
Iteraciones
Costo
0.2 0.6 0.2
20
135
$ 2,105,388.22 0.2 0.6
0.2
20
102
$ 2,557,869.65
0.2 0.4 0.4
20
104
$ 2,415,922.99 0.2 0.4
0.4
20
103
$ 2,571,503.31
0.2 0.2 0.6
20.1
103
$ 2,516,786.84 0.2 0.2
0.6
20
127
$ 2,499,594.34
0.4 0.4 0.2
20
193
$ 2,123,381.36 0.4 0.4
0.2
20
120
$ 2,169,704.35
0.4 0.2 0.4
20
148
$ 2,087,313.18 0.4 0.2
0.4
20
131
$ 2,428,844.79
0.6 0.2 0.2
20
201
$ 2,151,441.72 0.6 0.2
0.2
20
201
$ 2,136,414.46
R-28
Mc Mp Mpu
Presión
mínima
(m)
No.
Iteraciones
Costo
Mc Mpu Mir
Presión
mínima
(m)
No.
Iteraciones
Costo
0.2 0.6 0.2
15.4
36
$ 151,959.90 0.2 0.6
0.2
15.1
43
$ 156,859.10
0.2 0.4 0.4
15.4
36
$ 151,457.57 0.2 0.4
0.4
15
48
$ 155,926.60
0.2 0.2 0.6
15.4
36
$ 151,457.57 0.2 0.2
0.6
15
46
$ 155,181.22
0.4 0.4 0.2
15.3
41
$ 149,262.81 0.4 0.4
0.2
15
54
$ 156,307.22
0.4 0.2 0.4
15
50
$ 153,067.78 0.4 0.2
0.4
15
57
$ 156,761.85
0.6 0.2 0.2
15
60
$ 160,201.36 0.6 0.2
0.2
15
60
$ 157,506.74
Taichung
Mc Mp Mpu
Presión
mínima
(m)
No.
Iteraciones
Costo
Mc Mpu Mir
Presión
mínima
(m)
No.
Iteraciones
Costo
0.2 0.6 0.2
15.1
18
$ 8,967,185.30 0.2 0.6
0.2
15.1
19
$ 8,997,666.43
0.2 0.4 0.4
15.5
16
$ 8,922,693.36 0.2 0.4
0.4
15
22
$ 9,260,342.73
0.2 0.2 0.6
15.4
17
$ 9,006,920.42 0.2 0.2
0.6
15.2
20
$ 9,137,243.74
0.4 0.4 0.2
15.3
21
$ 9,062,582.70 0.4 0.4
0.2
15
22
$ 9,106,793.30
0.4 0.2 0.4
15.6
23
$ 9,117,528.80 0.4 0.2
0.4
15
23
$ 9,163,632.94

Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
87
0.6 0.2 0.2
15
27
$ 9,909,996.79 0.6 0.2
0.2
15
27
$ 10,219,346.44
COSTO-PUTI-RESILIENCIA
PRESIÓN-PUTI-INDICE RESILIENCIA
Hanoi
Mc Mp Mir
Presión
mínima
(m)
No.
Iteraciones
Costo
Mp Mpu Mir
Presión
mínima
(m)
No.
Iteraciones
Costo
0.2 0.6 0.2
32
28
$ 5,745,571.90 0.2 0.6
0.2
30.5
28
$ 5,765,197.26
0.2 0.4 0.4
30.6
28
$ 5,705,652.17 0.2 0.4
0.4
30.5
28
$ 5,765,197.26
0.2 0.2 0.6
30.6
28
$ 5,705,652.17 0.2 0.2
0.6
30.3
28
$ 5,863,975.33
0.4 0.4 0.2
30.9
28
$ 5,580,225.85 0.4 0.4
0.2
31.2
28
$ 5,778,105.72
0.4 0.2 0.4
31.6
29
$ 5,611,953.67 0.4 0.2
0.4
31.2
29
$ 5,778,105.72
0.6 0.2 0.2
30.4
30
$ 5,580,247.40 0.6 0.2
0.2
31.2
30
$ 5,778,105.72
Balerma
Mc Mp Mir
Presión
mínima
(m)
No.
Iteraciones
Costo
Mp Mpu Mir
Presión
mínima
(m)
No.
Iteraciones
Costo
0.2 0.6 0.2
20
142
$ 2,103,429.98 0.2 0.6
0.2
20
102
$ 2,557,869.65
0.2 0.4 0.4
20
119
$ 2,262,157.30 0.2 0.4
0.4
20.1
102
$ 2,566,825.16
0.2 0.2 0.6
20.1
118
$ 2,468,383.70 0.2 0.2
0.6
20.1
130
$ 2,478,009.85
0.4 0.4 0.2
20
192
$ 2,119,305.67 0.4 0.4
0.2
20.1
108
$ 2,626,988.33
0.4 0.2 0.4
20
153
$ 2,076,309.19 0.4 0.2
0.4
20
107
$ 2,848,368.58
0.6 0.2 0.2
20
201
$ 2,150,626.77 0.6 0.2
0.2
20.1
104
$ 2,581,581.00
R-28
Mc Mp Mir
Presión
mínima
(m)
No.
Iteraciones
Costo
Mp Mpu Mir
Presión
mínima
(m)
No.
Iteraciones
Costo
0.2 0.6 0.2
15.5
39
$ 151,164.61 0.2 0.6
0.2
15.4
34
$ 153,695.18
0.2 0.4 0.4
15
44
$ 152,697.17 0.2 0.4
0.4
15.9
36
$ 153,541.77
0.2 0.2 0.6
0.2 0.2
0.6
15
42
$ 155,725.32
0.4 0.4 0.2
15.2
51
$ 153,520.97 0.4 0.4
0.2
15.1
37
$ 152,362.42
0.4 0.2 0.4
15
49
$ 152,646.66 0.4 0.2
0.4
15.2
37
$ 151,036.12
0.6 0.2 0.2
15
60
$ 160,201.36 0.6 0.2
0.2
15.1
37
$ 152,362.42
Taichung
Mc Mp Mir
Presión
mínima
(m)
No.
Iteraciones
Costo
Mp Mpu Mir
Presión
mínima
(m)
No.
Iteraciones
Costo
0.2 0.6 0.2
15.1
20
$ 8,992,954.80 0.2 0.6
0.2
15.1
15
$ 8,867,681.95
0.2 0.4 0.4
15.3
23
$ 9,185,202.12 0.2 0.4
0.4
15.9
17
$ 8,940,378.26
0.2 0.2 0.6
15.1
23
$ 9,180,560.34 0.2 0.2
0.6
15.1
20
$ 8,936,881.69
0.4 0.4 0.2
15
22
$ 9,043,718.40 0.4 0.4
0.2
16.3
18
$ 8,986,417.73
0.4 0.2 0.4
15.1
23
$ 9,109,887.29 0.4 0.2
0.4
15.1
18
$ 8,813,021.79
0.6 0.2 0.2
15
25
$ 9,709,552.80 0.6 0.2
0.2
15.9
19
$ 9,071,440.20
Tabla 20. Prueba del escenario de tres factores para el calculador Epanet.
Universidad de los Andes
Departamento de Ingeniería Civil y Ambiental
Centro de Investigaciones en Acueductos y Alcantarillados – CIACUA
Algoritmo de redondeo de diámetros dentro del módulo de diseño del
programa redes
PIC 2013-20
Juan Felipe García
Tesis Pregrado
88
SPARSE SOLVER
Hanoi
Mc
Mp
Mpu
Mir
Presión mínima
(m)
No. Iteraciones
Costo
0.2
0.4
0.2
0.2
30.59
1257
$ 5,705,652.17
0.2
0.2
0.4
0.2
30.59
1243
$ 5,705,652.17
0.2
0.2
0.2
0.4
30.24
1273
$ 5,777,764.84
0.4
0.2
0.2
0.2
31.55
1197
$ 5,611,953.67
R-28
Mc
Mp
Mpu
Mir
Presión mínima
(m)
No. Iteraciones
Costo
0.2
0.4
0.2
0.2
15.04
4714
$ 150,398.18
0.2
0.2
0.4
0.2
15.26
4752
$ 151,545.53
0.2
0.2
0.2
0.4
15.09
3009
$ 157,463.53
0.4
0.2
0.2
0.2
15.02
3403
$ 154,214.47
Taichung
Mc
Mp
Mpu
Mir
Presión mínima
(m)
No. Iteraciones
Costo
0.2
0.4
0.2
0.2
15.99
1898
$ 9,143,774.33
0.2
0.2
0.4
0.2
15.06
1871
$ 9,161,195.10
0.2
0.2
0.2
0.4
15
1862
$ 9,060,276.76
0.4
0.2
0.2
0.2
15.76
1869
$ 9,194,179.33
Tabla 21. Prueba del escenario de cuatro factores para el calculador SparseSolver.
EPANET
Hanoi
Mc
Mp
Mpu
Mir
Presión
mínima (m)
No. Iteraciones
Costo
0.2
0.4
0.2
0.2
30.4
28
$ 5,705,652.17
0.2
0.2
0.4
0.2
3034
27
$ 5,736,632.53
0.2
0.2
0.2
0.4
30.34
27
$ 5,736,632.53
0.4
0.2
0.2
0.2
30.01
28
$ 5,600,890.84
Balerma
Mc
Mp
Mpu
Mir
Presión
mínima (m)
No. Iteraciones
Costo
0.2
0.4
0.2
0.2
20.01
108
$ 2,366,863.37
0.2
0.2
0.4
0.2
0.2
0.2
0.2
0.4
20
114
$ 2,474,785.61
0.4
0.2
0.2
0.2
20.01
155
$ 2,076,064.20
R-28
Mc
Mp
Mpu
Mir
Presión
mínima (m)
No. Iteraciones
Costo
0.2
0.4
0.2
0.2
15.23
37
$ 149,586.65
0.2
0.2
0.4
0.2
15.13
37
$ 150,314.32
0.2
0.2
0.2
0.4
15.04
52
$ 154,057.91
0.4
0.2
0.2
0.2
15.01
52
$ 153,451.68
Taichung
Mc
Mp
Mpu
Mir
Presión
mínima (m)
No. Iteraciones
Costo
0.2
0.4
0.2
0.2
15.21
21
$ 8,922,582.24
0.2
0.2
0.4
0.2
15.44
17
$ 8,914,577.24
0.2
0.2
0.2
0.4
15.14
23
$ 9,180,560.34
0.4
0.2
0.2
0.2
15.33
21
$ 9,062,582.70
Tabla 22. Prueba del escenario de cuatro factores para el calculador Epanet.
