
IAHR
CIC
XXV CONGRESO LATINOAMERICANO DE HIDRÁULICA
SAN JOSÉ, COSTA RICA, 9 AL 12 DE SEPTIEMBRE DE 2012
MODELACIÓN FÍSICA DE CAMBIOS OPERATIVOS EN REDES DE
DISTRIBUCIÓN DE AGUA POTABLE: MODELACIONES EN PERÍODO
EXTENDIDO Y MODELACIÓN DE FLUJO NO PERMANENTE
Juan Saldarriaga Valderrama
1
, Iván Camilo Viveros Góngora
2
Profesor Titular de la Universidad de Los Andes, Colombia, jsaldarr@uniandes.edu.co
1
Estudiante de Pregrado de la Universidad de Los Andes, Colombia, ic.viveros317@uniandes.edu.co
2
RESUMEN:
En la red elevada del Laboratorio de Hidráulica y Recursos Hídricos de la Universidad de
los Andes se construyeron cuatro configuraciones hidráulicas (escenario 5 inicial, escenario 5 final,
escenario 6 inicial y escenario 6 final), se midieron presiones en nueve puntos y caudales en tres
puntos. Los programas EPANET y REDES en modelación de estado estable representaron la
variabilidad con índices de r
2
superiores a 0.90 y errores cuadráticos medios inferiores a 0.12.
Con el fin de analizar los perfiles de presión y caudal, producto de una variación brusca que
indujera transientes, los escenarios se agruparon en pares de tal manera que la transición de un
escenario a otro requiriera únicamente del cierre súbito de una válvula de bola. A partir de los datos
de campo se calcularon patrones de demanda en los nodos de extracción de caudal y de energía
disponible al inicio de la red.
El modelo en período extendido del escenario 5 representó la variabilidad y la magnitud de
los datos satisfactoriamente (r
2
=0.95 y error cuadrático medio=0.07). Por otro lado, el escenario 6
presentó indicadores estadísticos poco satisfactorios (r
2
=0.95 y error cuadrático medio=1.09). Una
vez se retiraron del análisis los datos relacionados con el punto de presión aislado y desabastecido
después del cierre de la válvula, se obtuvieron indicadores representativos (r
2
=0.95 y error
cuadrático medio=0.08).
ABSTRACT:
In the drinking water pipe network located in the Laboratory of Hydraulics and Water
Resources at Los Andes University were set four hydraulic configurations (escenario 5 inicial,
escenario 5 final, escenario 6 inicial y escenario 6 final). Pressure (in 9 points) and caudal (in 3
different points) were measured. EPANET and REDES steady simulations had satisfactory
statistical indexes (r
2
over 0.90 and root mean square error RMS under 0.12).
In order to analyze pressure and caudal profiles after a sudden variation that led transients,
configurations were clustered in pairs. Abrupt change from initial to final arrangements consisted of
closing a ball valve in a short period of time. Based on laboratory data, caudal and initial energy
patterns were calculated.
Simulations in extended period proved to represent adequately laboratory data related to
“escenario 5” configuration (r
2
=0.95 and RMS=0.07). Second configuration had unsatisfactory
statistical outputs (r
2
=0.95 and RMS=1.09). When data from isolated area was retired, statistical
proficiency of model became representative (r
2
=0.95 and RMS=0.08).
PALABRAS CLAVES: transiente de presión; representatividad

INTRODUCCIÓN
Uno de los objetivos de este estudio estaba enfocado en analizar las variaciones de presión y
demanda en puntos distribuidos en una red de distribución de agua potable antes, durante y después
de un cambio operativo súbito que indujera un transiente de presión. Otro objetivo consistía en
analizar la representatividad de EPANET y REDES en estado estable y período extendido, con
respecto a los datos experimentales.
En los sistemas de distribución de agua, el control del caudal es esencial para su adecuada
operación. Rápidos cambios operativos pueden inducir transientes de presión. Éstos pueden afectar
de manera negativa el sistema de distribución si no son controlados (Magzoub Elbashir & Kwame
Amoah, 2007).
Los transientes están clasificados como flujo variado no permanente, es decir, sus
características hidráulicas varían con respecto al espacio y al tiempo (Saldarriaga, 2007). Los
rápidos tránsitos de presión ocurren cuando el estado estable del flujo es alterado (Bosserman II &
Hunt, 2006). La ocurrencia del fenómeno está relacionada con cierres súbitos de válvulas, fallas del
sistema de control, pérdida de potencia, pérdida de telemetría, interacción de servicios múltiples,
inadecuada selección de equipos, cambios en la demanda, intrusión de aire, fallas en los sistemas de
regulación de presión y ruptura de tubos (Stone, 2006) (Bosserman II & Hunt, 2006).
Una vez ocurre un cambio operativo súbito los segmentos del fluido más alejados del evento
tienden a conservar el momentum mientras que los más cercanos son influenciados rápidamente por
la variación. Esto implica una disminución de la presión. El cambio repentino insta al sistema a
buscar el equilibrio, lo cual resulta en fluctuaciones que pueden verse modificadas por la presencia
de aire o gases, la superposición de ondas y la propagación de las ondas de tensión en el material de
la tubería (Thorley, 1991).
La magnitud de las variaciones de presión (
) ha sido relacionada con la celeridad de la
onda (
), la diferencia entre las velocidades en estado estable ( ) y la gravedad ( ) [1]
(Joukowsky, 1900). La celeridad de la onda ha sido explicada a través del módulo de
compresibilidad (
) y la densidad ( ) del fluido, el módulo de elasticidad del material ( ), el
diámetro (
) y la rugosidad ( ) de la tubería [2] (Korteweg, 1878). Se asume que por cada
que sea forzado a detenerse de manera súbita, hay variaciones entre 345kPa y 414 kPa (Kirmeyer, y
otros, 2001).
[1]
√
(
) (
)
[2]
Debido a la superposición de ondas se han reportado transientes que superan los valores
pronosticados por la ecuación [1] (Simpson & Wylie, 1991) (Thorley, 1991).
La importancia de los estudios relacionados con los transientes de presión en redes de
distribución de agua potable radica parcialmente en sus consecuencias. El fenómeno puede implicar
resuspensión de partículas sedimentadas, desprendimiento de biopelículas, intrusión de elementos
externos, desmejoramiento de la calidad del agua, cavitación, vibraciones, ruptura, desplazamiento
y deformación de las tuberías (Wood, 2005) (Bosserman II & Hunt, 2006).
En el suelo y el agua al exterior del sistema de distribución de agua potable se han detectado
indicadores fecales y virus humanos; sin embargo, no hay suficiente información para afirmar que
los transientes representan un riesgo significativo para la salud humana, en parte porque los
sistemas de monitoreo no consideran las zonas vulnerables a presiones bajas y no cuentan con
equipos de medición de alta frecuencia (LeChevallier, Gullick, Karim, Friedman, & Funk, 2003).
El estudio descrito en este texto evaluó 4 escenarios en estado estable, los cuales presentaron
resultados satisfactorios de representatividad. La modelación en período extendido se realizó con
datos de una variación operativa brusca desde un escenario inicial a un escenario final; a excepción
de las zonas aisladas se obtuvo una representatividad satisfactoria.
MODELOS COMPUTACIONALES
EPANET y REDES fueron los programas computacionales que fueron utilizados para llevar
a cabo las simulaciones. EPANET modela el comportamiento del agua en sistemas de tuberías
presurizadas a través del método del gradiente y permite la introducción de accesorios como
válvulas y tanques. El programa REDES fue desarrollado en el Centro de Investigaciones en
Acueductos y Alcantarillados (CIACUA) del departamento de Ingeniería Civil y Ambiental de la
Universidad de Los Andes. REDES está programado bajo el paradigma orientado por objetos, su
lenguaje computacional es Delphi, usa el método de cálculo del gradiente y resuelve el sistema
matricial a través de la factorización de Cholesky (Saldarriaga, 2007).
Para las simulaciones se utilizó un modelo de la red elevada del Laboratorio de Hidráulica y
Recursos Hídricos de la Universidad de Los Andes, el cual en su proceso de construcción contó con
levantamientos topológicos y topográficos. Adicionalmente, sus coeficientes de pérdidas menores
fueron calibrados y validados (Prieto Gamboa, 2011).
MODELACIÓN EN ESTADO ESTABLE
Es relevante especificar qué parámetros fueron introducidos en los modelos en estado
estable. La energía de entrada o altura del embalse correspondió al valor promedio de las
mediciones en el punto de presión A. Las demandas base en los puntos de extracción de caudal
fueron determinadas por medio de métodos volumétricos en la red. El material de los tubos es PVC,
por ende todos los segmentos de la red en el modelo cuentan con rugosidades de 0.0015mm. La
longitud de los segmentos, coordenadas de los puntos y coeficientes de pérdidas menores fueron
retomados de modelos previos (Prieto Gamboa, 2011).
La red elevada utilizada para el procedimiento experimental cuenta con tuberías de 4
pulgadas, 3 pulgadas y 2 pulgadas. El sistema posee válvulas de bola de 2 pulgadas las cuales
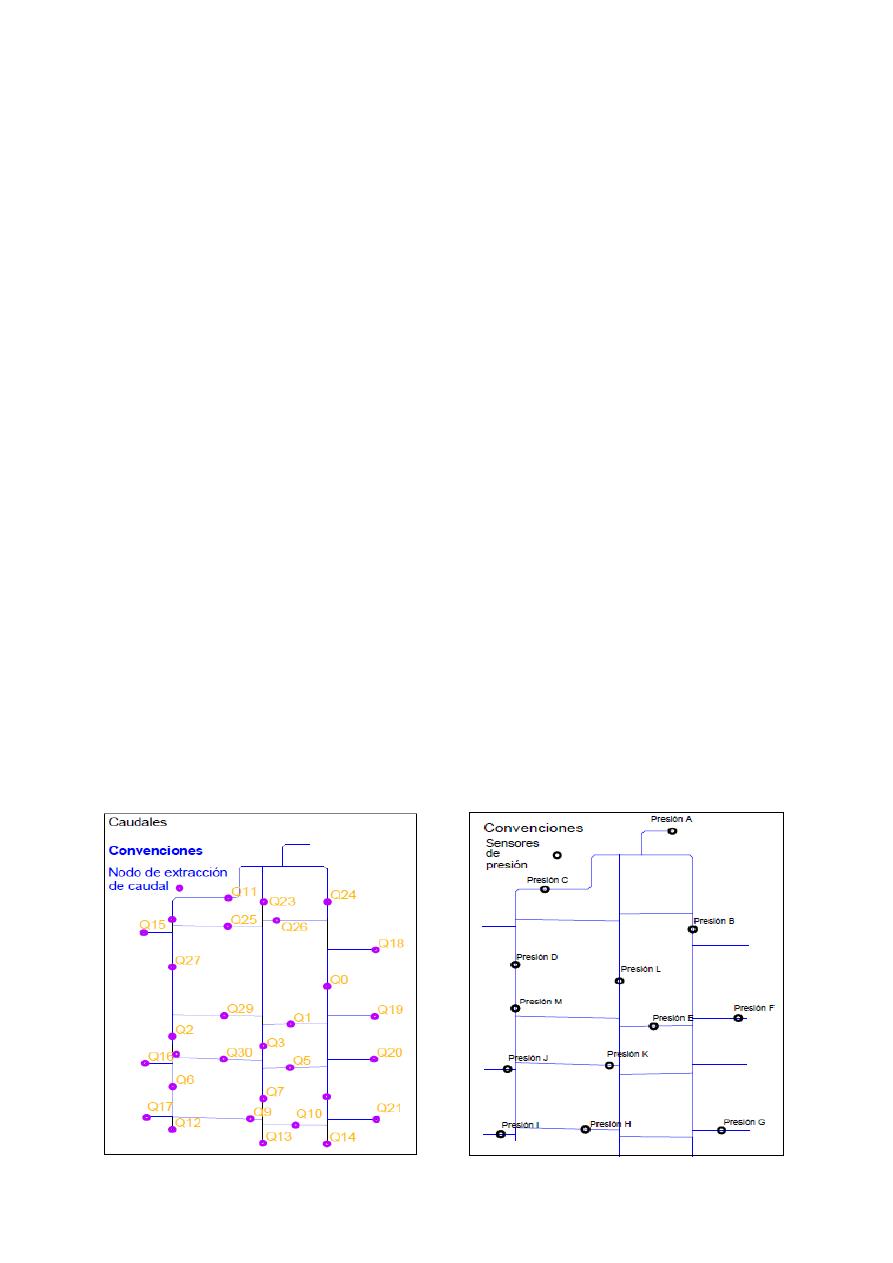
permiten extraer caudal y cuya nomenclatura puede ser consultada en la figura 2. La red dispone de
13 puntos con disponibilidad para instalar sensores de presión (ver figura 3) en este estudio
únicamente se utilizaron 9 (A, B, C, D, E, F, G, H, I). Para modificar la dirección del flujo o
determinar una nueva configuración hidráulica la red cuenta con válvulas de 2, 3 y 4 pulgadas. El
material de las tuberías es PVC.
Figura 1.- Nodos de Extracción de Caudal
Figura 2.- Sensores de Presión

Figura 3.- Escenario 5 Inicial
Figura 4.- Escenario 5 Final
Figura 5.- Escenario 6 Inicial
Figura 6.- Escenario 6 Final
Los escenarios sometidos a procesos de medición son el escenario 5 inicial (figura 4), el
escenario 5 final (figura 5), el escenario 6 inicial (figura6) y el escenario 6 final (figura 7). La
diferencia entre los escenarios iniciales y finales radica en el cierre súbito de una válvula.
Para calcular las demandas en los nodos se usaron baldes de 10.90L y 10.94L. Con un
cronómetro se contabilizaba el tiempo de llenado. El volumen de agua dividido sobre el tiempo,
permitía determinar el caudal. El procedimiento se repitió 10 veces y con base en los valores se
determinaron promedios. La mayor desviación estándar de caudales se obtuvo en el Escenario 5
Final, en el nodo Q15 con una magnitud de 0.07
.
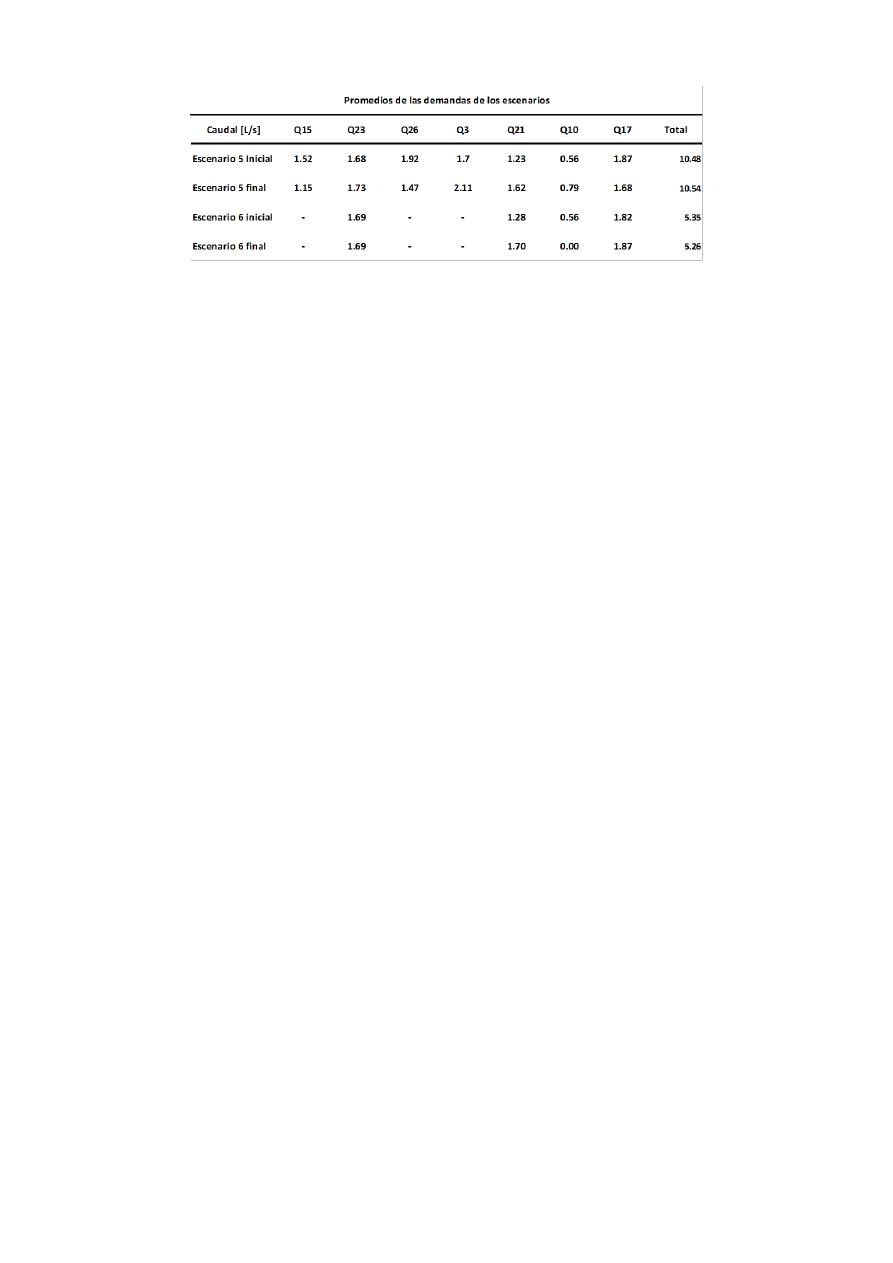
Los promedios de los caudales calculados fueron introducidos en los nodos de extracción de
caudal del modelo como demandas base. Por ejemplo, el escenario 6 inicial en las uniones Q23,
Q21, Q10 y Q17, tuvo demandas base con valores de 1.69
, 1.28
, 0.56
y1.82
respectivamente.
Tabla 1.-Promedios de las Demandas de los Escenarios
Las presiones fueron medidas a través de sensores de presión: 5 instrumentos contaban con
rangos de medición de 0 a 1 bar (MAN-SD2S B2 de Kobold y Vegabar 52) y 4 instrumentos tenían
rangos de medición de -1 a 5 bar (MAN LD3S de Kobold). Los últimos, fueron adquiridos para
instalarlos en los puntos de mayor variabilidad de presión. Los 9 sensores estaban conectados a una
red que conduce a un fieldpoint (FP-1601) el cual transmitía los datos a un programa computacional
del laboratorio. El programa sincronizaba y reportaba los valores medidos.
El procedimiento para medir consistía en cerrar las válvulas y abrir los nodos para construir
alguno de los escenarios a medir. Se permitía durante 15 minutos que el sistema estabilizara las
condiciones hidráulicas. Posteriormente se medía durante 10 minutos la presión en los 9 puntos
correspondientes.
MODELACIÓN EN PERÍODO EXTENDIDO
La modelación en período extendido tenía como finalidad simular el cambio súbito de un
escenario a otro y compararla con los datos de laboratorio. Las variaciones consistían en construir el
escenario inicial y a través del cierre súbito de una válvula cuya clausura duraba aproximadamente
0.64 milésimas de segundo, se construía el escenario final.
La rugosidad, las coordenadas de las uniones, las longitudes de las tuberías, la rugosidad y
las pérdidas menores en la modelación en período extendido tenían las mismas características que
en estado estable. Sin embargo, la energía de entrada (o altura del embalse) y las demandas de los
nodos de extracción de caudal poseían patrones calculados a partir de las mediciones.
El primer paso en el proceso de medición consistía en configurar los relojes de los equipos
que iban a ser utilizados y construir alguno de los escenarios iniciales. Se instalaba el caudalímetro
en alguna de las tres ubicaciones. Se le permitía a la red estabilizarse durante 15 minutos, después
se medía el caudal y las presiones en alguno de los escenarios iniciales durante 15 minutos, se
cerraba la válvula de manera súbita y se registraba el tiempo en el cual esto ocurría. Después de la
variación se medían los parámetros 15 minutos como mínimo. Desde que inicia la medición en el
escenario inicial hasta que se estabiliza el escenario final, la medición no tuvo pausas.
La presión fue medida a través de los 9 sensores y los datos fueron registrados en el
programa computacional mencionado previamente. El caudal se midió con un caudalímetro no
intrusivo Ultraflux UF-801-P. Éste fue ubicado en tres diferentes tuberías que alimentaban nodos de
extracción de caudal. La ubicación 1 corresponde a una tubería que alimentaba el nodo de
extracción de caudal Q17, la ubicación 2 correspondía a Q21 y la ubicación 3 estaba relacionada
con Q10 (ver figura 7). Los demás puntos desde donde se extraía caudal, difícilmente podían ser
medidos debido a las distancias mínimas requeridas por equipo. Puesto que se contaba con tres
ubicaciones, las variaciones de los escenarios 5 y los escenarios 6 se realizaron tres veces cada una.
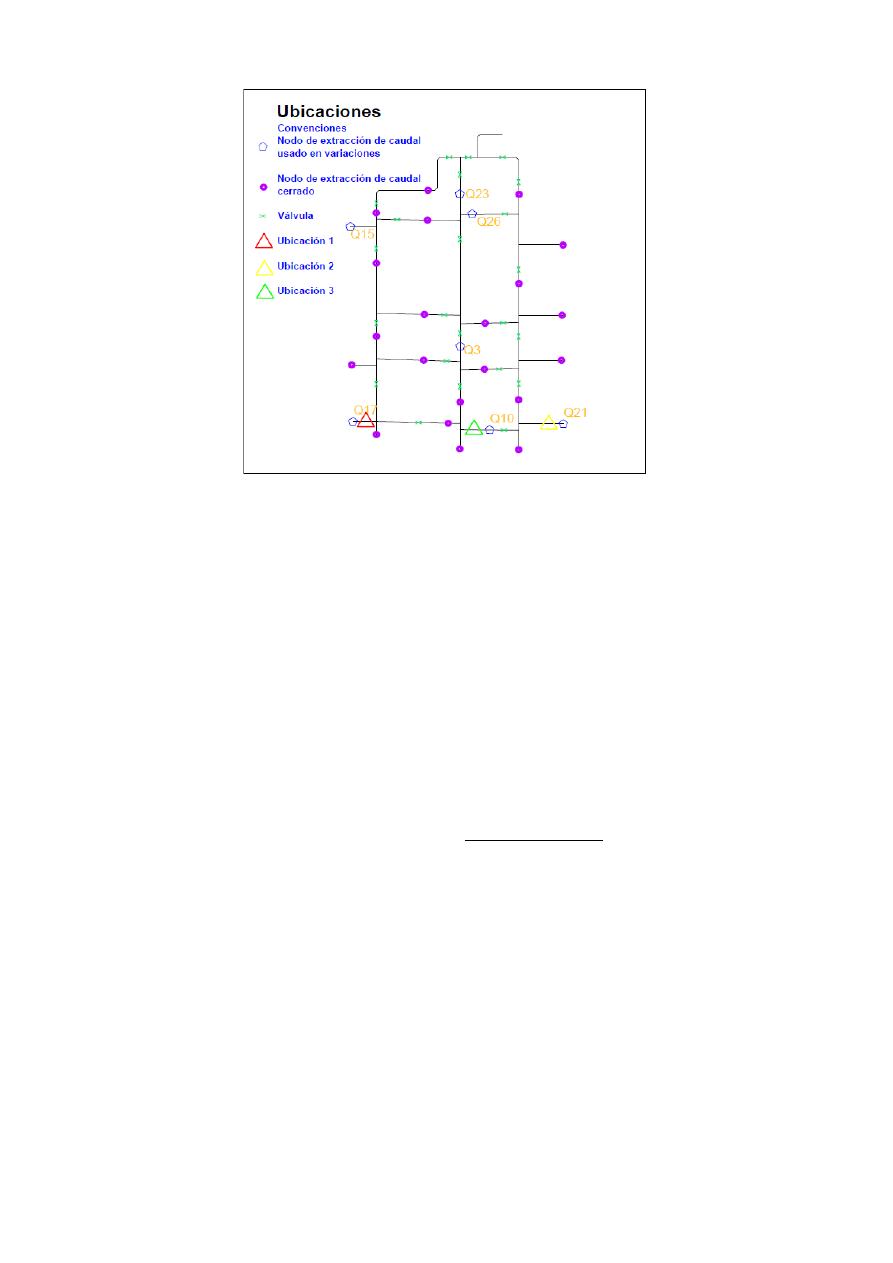
Figura 7.- Ubicaciones del Caudalímetro
Se poseía información sobre variaciones de la presión en 9 puntos y del caudal en 3 puntos
de la red, suficiente para calcular patrones de energía de entrada y de demanda en Q17, Q10 y Q21.
Sin embargo, era necesario realizar suposiciones para aquellas uniones que no fueron sometidas a
medición (Q15, Q23, Q3 y Q26). Los patrones de Q17 fueron aplicados a Q15 y Q23. Los patrones
de Q21 fueron aplicados a Q3 y a Q26. Los patrones para la altura del embalse o la energía inicial
fueron determinados a partir de los datos del punto de presión A.
En la altura base del embalse y la demanda base se introdujeron los valores promedio de las
mediciones de variación, excepto para los nodos Q15, Q23, Q3 y Q26, los cuales mantuvieron los
valores de demanda base de los escenarios iniciales en estado estacionario. El intervalo temporal de
medición fue de 1 segundo mientras que en los programas es de 1 minuto. Por este motivo, se
calcularon los promedios de todos los segundos de cada minuto y se asumió ese valor.
La demanda base correspondía al promedio de los datos de caudal y la altura base del
embalse a los promedios de la presión A. Sin embargo, era necesario adicionar factores
multiplicadores que permitieran la variación en el tiempo [3].
[3]
RESULTADOS
Se puede afirmar que los modelos computacionales sometidos a análisis en estado estable
representaron la variabilidad y se desviaron de manera leve con respecto a los valores de
laboratorio. Obsérvense los coeficientes de determinación, todos poseen magnitudes superiores a
0.94. Los errores cuadráticos medios en todos los casos presentaron valores inferiores a 0.11
(tabla2).
Los resultados de la modelación en período extendido para la variación del escenario 5
inicial al escenario al escenario 5 final sugirieron representatividad y poca desviación con respecto
a los valores de laboratorio (tabla 3, fila 1). Por el contrario, la variación del escenario 6 inicial al
escenario 6 final presentó poca representatividad de la variabilidad y una significativa desviación
con respecto a las mediciones experimentales (tabla 3, fila 2).
El escenario 6 final debido a sus características, aislaba e impedía el flujo hacia una de las
zonas donde se realizaban mediciones de presión (el punto H). Por este motivo, se decidió remover
del análisis los datos del punto H. Tanto el coeficiente de determinación como el error cuadrático
medio (tabla 3, fila 3) presentaron magnitudes satisfactorias en las nuevas circunstancias.
Tabla 2.- Indicadores Estadísticos de Modelación en Estado
Estable
Tabla 3.- Indicadores Estadísticos de
Modelación en Período Extendido
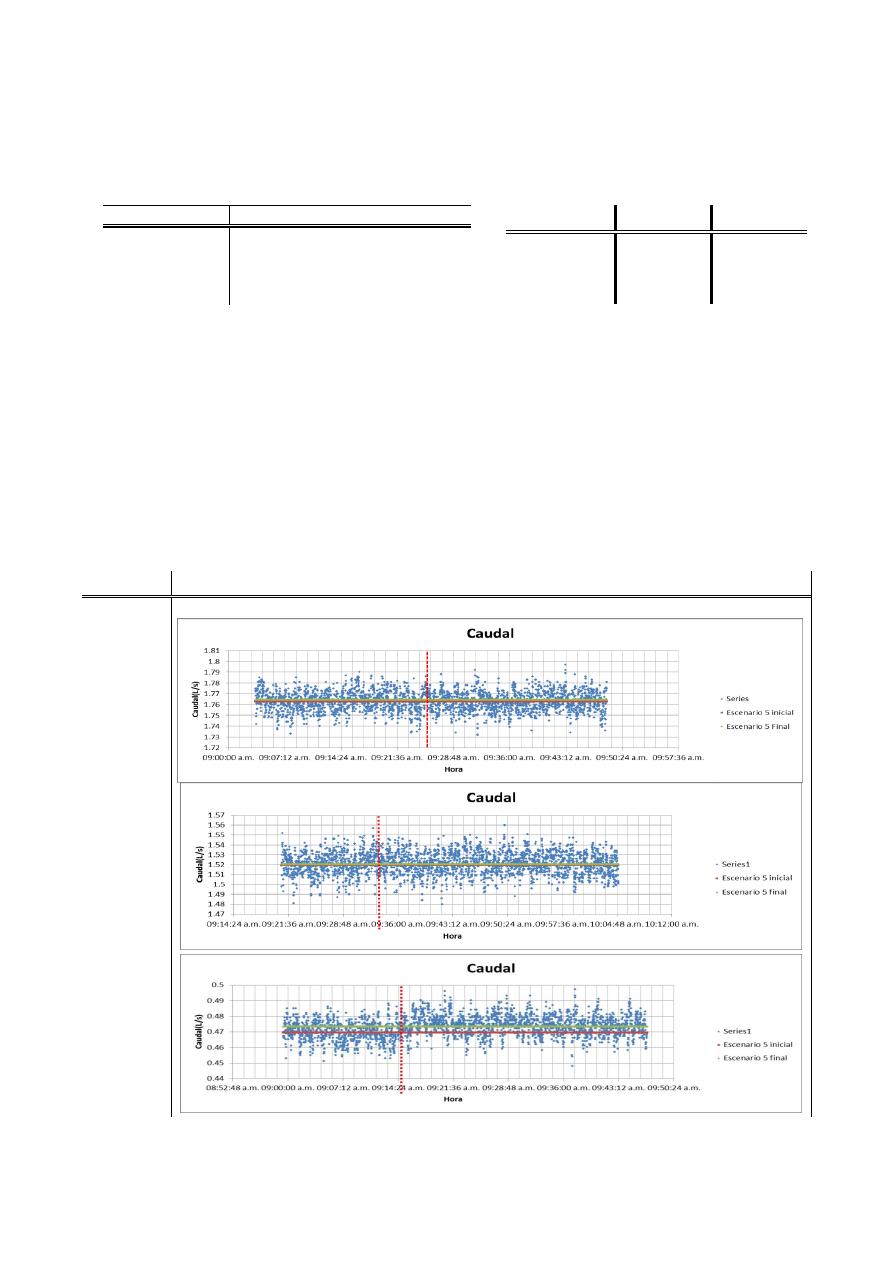
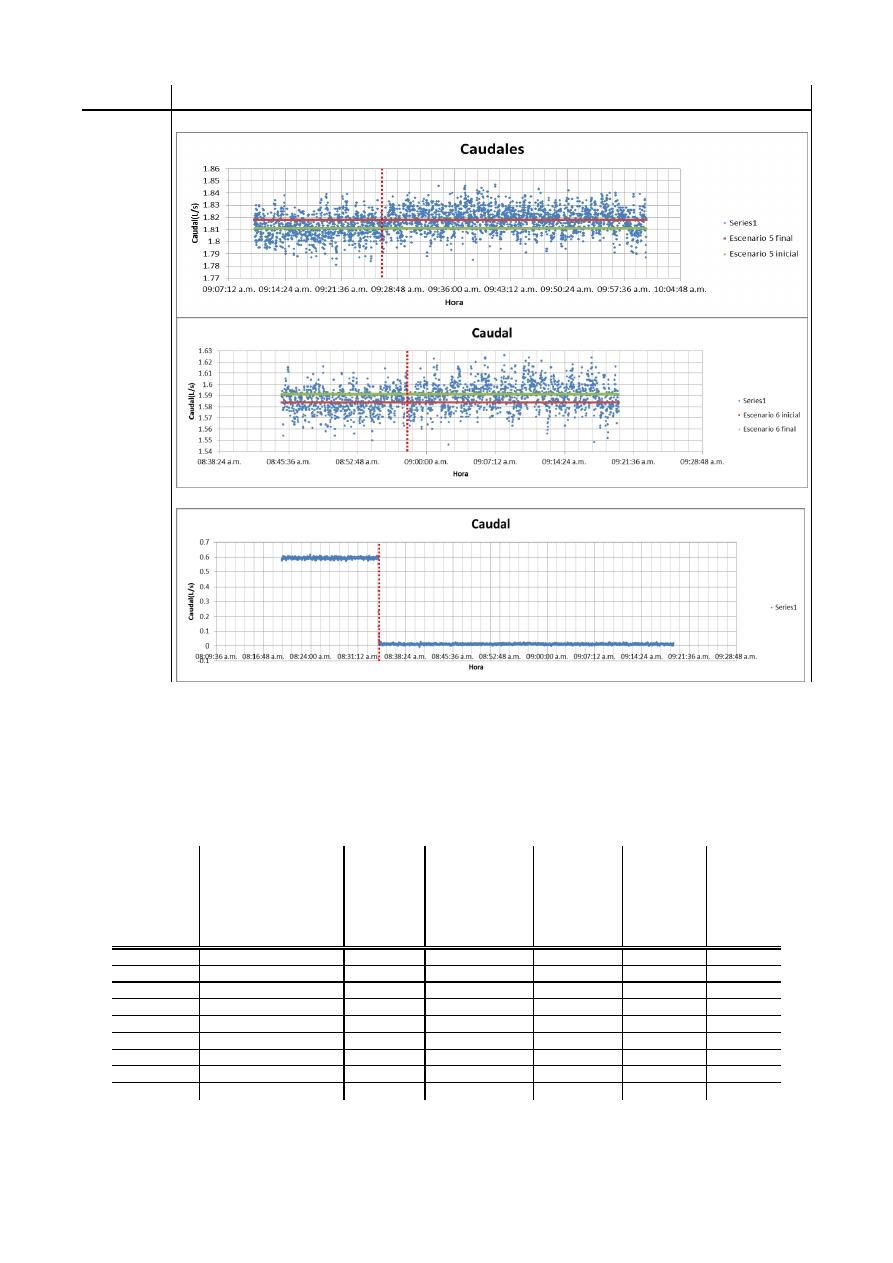
Las tablas 4 y 5 presentan los resultados de las mediciones de caudal en las diferentes
ubicaciones. Las asíntotas horizontales representan los promedios de los escenarios iniciales y
finales. Las asíntotas de color rojo indican el momento en el que se efectuó el cierre súbito de la
válvula. La variación del escenario 5 inicial al escenario 5 final presenta perfiles de caudal cuyas
medias difieren muy poco antes y después del cambio; inclusive las variaciones entre las medias se
mantienen dentro del rango de dispersión de los datos. En las variaciones del escenario 6 inicial al
escenario 6 final, en las ubicaciones 1 y 2, la diferencia entre las medias se encuentra dentro del
rango de variación, sin embargo se puede apreciar un período de transición del escenario inicial al
escenario final de 3 a 5 minutos. En la ubicación 3, debido a que el caudalímetro se localizaba en
una zona que después de la variación quedaba desabastecida, el cambio de tendencias es inmediato.
Tabla 4.- Perfiles de Caudales de las Variaciones del Escenario 5
Variación Escenario 5
Ubicación
1
Ubicación
2
Ubicación
3
Tabla 5.- Perfiles de Caudales de las Variaciones del Escenario 6
[m.c.a]
R2
R.M.S
Escenario 5 inicial
0.96
0.11
Escenario 5 final
0.96
0.11
Escenario 6 inicial
0.97
0.07
Escenario 6 final
0.94
0.08
Indicadores Estadísticos
R
2
R.M.S
Escenario 5
0.95
0.07
Escenario 6
0.15
1.09
Escenario 6
*
0.95
0.08
Variación Escenario 6
Ubicación
1
Ubicación
2
Ubicación
3
Una vez fueron obtenidos los valores de presión, el escenario 5 no presentó máximos o
mínimos notablemente fuera del rango de dispersión y/o temporalmente relacionados con la
variación. La variación del escenario 6 inicial, al 6 final presentó máximos temporalmente cercanos
al cierre de válvula; la diferencia entre el máximo y el escenario final superaba en todos los casos la
dispersión de los escenarios iniciales y finales (tablas 6,7 y 8).
Tabla 6.- Máximos Valores de Presión Escenario 6 ubicación 1
Tabla 7.- Máximos Valores de Presión Escenario 6 ubicación 2
Valores máximos (M.C.A)
Hora
Diferencia Absoluta
entre el Tiempo del
Valor máximo y el
Tiempo de Cierre
de la Válvula (s)
Diferencia entre
el Valor Máximo
y el Promedio
del Escenario 6
Final (M.C.A)
Desviación
Estándar
Escenario 6
Inicial(M.C.A)
Desviación
Estándas
Escenario 6
Final (M.C.A)
Presión A
4.4153
09:37:37 a.m.
636
0.0051
0.0011
0.0010
Presión B
4.4456
09:27:01 a.m.
3
0.1130
0.0011
0.0010
Presión C
4.6761
09:27:01 a.m.
3
0.2204
0.0094
0.0076
Presión D
4.1131
09:27:01 a.m.
3
0.1867
0.0071
0.0091
Presión E
4.5371
09:27:01 a.m.
3
0.2509
0.0069
0.0056
Presión F
3.9468
09:27:01 a.m.
3
0.0453
0.0083
0.0070
Presión G
3.8982
09:27:01 a.m.
3
0.1408
0.0052
0.0057
Presión H
3.8072
09:26:58 a.m.
1
3.9342
0.0009
0.0000
Presión I
3.8184
09:27:01 a.m.
3
0.1628
0.0120
0.0043
Tabla 8.- Máximos Valores de Presión Escenario 6 ubicación 3
CONCLUSIONES
EPANET y REDES contaron con una representatividad satisfactoria de los escenarios
hidráulicos propuestos en estado estable. La modelación en período extendido simuló con
representatividad satisfactoria las variaciones bruscas de escenarios que consistían en el cierre
súbito de una válvula. Sin embargo, aquéllas zonas aisladas y sometidas a desabastecimiento no
fueron adecuadamente representadas en los modelos.
Los perfiles de presión de la variación del escenario 5 no presentaron en la mayoría de los
casos aumentos o disminuciones significativos, posteriores al cambio del escenario inicial y final.
Por otro lado, los perfiles de la variación del escenario 6 permiten contemplar máximos
temporalmente relacionados con el cierre súbito de la válvula. Los máximos se presentaron fuera
de los rangos de dispersión de datos.
Los perfiles de caudal del escenario 5 presentaron variaciones entre las medias del escenario
inicial y final de poca magnitud y no diferenciables del rango de variación de los datos. Esto
dificulta la identificación de un período de estabilización. En el escenario 6 aunque la diferencia
entre los promedios del escenario inicial y el escenario final también se encontraba dentro del rango
Valor
Máximo(M.C.A)
Hora
Diferencia Absoluta
entre el Tiempo del
Valor máximo y el
Tiempo de Cierre
de la Válvula (s)
Diferencia
entre el Valor
Máximo y el
Promedio del
Escenario 6
Final (M.C.A)
Desviación
Estándar
Escenario 6
Inicial
(M.C.A)
Desviación
Estándas
Escenario 6
Final
(M.C.A)
Presión A
4.346
08:58:28 a.m.
4
0.056
0.001
0.001
Presión B
4.289
08:58:28 a.m.
4
0.080
0.001
0.001
Presión C
2.658
08:58:28 a.m.
4
0.046
0.004
0.005
Presión D
4.323
08:58:27 a.m.
3
0.153
0.006
0.005
Presión E
3.853
08:58:27 a.m.
3
0.119
0.008
0.014
Presión F
3.929
08:58:30 a.m.
6
0.106
0.011
0.017
Presión G
3.772
08:58:28 a.m.
4
0.122
0.007
0.006
Presión H
08:51:08 a.m.
412
0.003
0.001
0.000
08:51:28 a.m.
392
08:51:29 a.m.
391
08:52:02 a.m.
358
Presión I
3.711
08:58:29 a.m.
5
0.132
0.005
0.003
3.700
Valores
Máximos
(M.C.A)
Hora
Diferencia
Absoluta entre
el Tiempo del
Valor máximo y
el Tiempo de
Cierre de la
Válvula (s)
Diferencia
Absoluta entre el
Valor Máximo y
el Promedio del
Escenario 6 Final
(M.C.A)
Desviación
Estándar
Escenario 6
Inicial
(M.C.A)
Desviación
Estándar
Escenario 6
Final (M.C.A)
Presión A
4.335
08:34:24 a.m.
5
0.010
0.001
0.001
Presión B
4.277
08:34:24 a.m.
5
0.028
0.001
0.001
Presión C
4.416
08:35:27 a.m.
68
0.039
0.009
0.009
Presión D
4.223
08:40:58 a.m.
399
0.012
0.006
0.006
08:41:26 a.m.
427
08:42:05 a.m.
466
08:42:49 a.m.
510
08:42:50 a.m.
511
08:55:44 a.m.
1285
09:04:03 a.m.
1784
Presión E
3.838
08:35:49 a.m.
90
0.045
0.016
0.013
Presión F
3.949
08:36:28 a.m.
129
0.112
0.012
0.017
Presión G
3.706
08:34:24 a.m.
5
0.026
0.007
0.005
Presión H
3.749
08:19:36 a.m.
883
3.874
0.001
0.000
Presión I
3.605
>40 registros
-
0.021
0.006
0.004

de variación de los datos, se puede apreciar una transición que toma de 3 a 5 minutos. En las zonas
sin abastecimiento de agua en el escenario final, la estabilización es inmediata.
Se podría estudiar a futuro la precisión de los modelos computacionales en período
extendido para zonas desabastecidas, la influencia de los nodos afectados por cambios operativos
súbitos y de las ramificaciones de las configuraciones hidráulicas sobre las magnitudes de los
transientes en las redes de distribución de agua potable.
REFERENCIAS BIBLIOGRÁFICAS
Bergant, A., Simpson, A. and Tijsseling, A. (2006). "Water hammer with column separation: A
historical review”. Journal of Fluids and Structures. Journal of Fluids and Structures, Vol. 22, pp
135-171.
Bosserman II, B. and Hunt, W. (2006). Pumping Station Design. G. Jones, Ed, Estados Unidos de
América.
Giustolizi, O., Kapelan, Z. and Savic, D. (2008). "Extended Period Simulation Analysis
Considering Valve Shutdowns". Journal of Water Resources Planning and Management, ASCE,
Vol.134, No.7, pp. 527-537.
Joukowsky, N. (1900). "Über den hydraulischen Stoss in Wasserleitungsröhren". Mémoires de
l’Académie Impériale des Sciences de St.-Pétersbourg, pp. 1-71.
Kirmeyer, G. J., Friedman, M., Martel, K., Howie, D., LeChevallier, M., Abbaszadegan, M., Karim,
M., Funk, J. and Harbour, J.(2001). Pathogen Intrusion into the Distribution System. AWWA
Research Foundation and American Water Works Association, Estados Unidos de América.
Korteweg, D. (1878). "Ueber die Fortpflanzungsgeschwindigkeit des Schalles in elastischen
Röhren". Annalen der Physik und Chemie, New Series 5, pp.525–542.
LeChevallier, M. W., Gullick, R. W., Karim, M. R., Friedman, M., & Funk, J. E. (2003). "The
Potential Risk from Intrusion of Contaminants into the Distribution System from Pressure
Transients". Journal of Water Health, Vol.1, No.1, pp.3-14.
Magzoub Elbashir, M. A. and Kwame Amoah, S. O. (2007). Hydraulic Transient in a Pipeline.
Lund University, Lund, Suecia.
Prieto Gamboa, C. M. (2011). Modelación física y calibración de sustancias en redes de
distribución de agua potable. Universidad de Los Andes, Bogotá, Colombia.
Saldarriaga, J. (2007). Hidráulica de Tuberías. Alfaomega-Uniandes, Colombia.
Simpson, A. and Wylie, B. (1991). "Large Water-Hammer Pressure for Column Separation in
Pipelines". Journal of Hydraulic Engineering, ASCE, Vol.117, No.10, pp.1310-1316.
Stone, G. (2006). "Contractual and Physical Risks from Waterhammer". World Pumps, Vol.2006,
No.473, pp.34, 37.38.
Thorley, A. (1991). Fluid Transients in Pipeline Systems. D. & L. George, Inglaterra.
Wood, D. (2005). "Waterhammer Analysis—Essential and Easy (and Efficient)". Journal of
Environmental Engineering, ASCE, Vol.131, No.8, pp.1123–1131.
